任务18：时间序列的模型-海口c网

任务描述

知识点：

移动平均法
指数平滑法
ARIMA模型

重点：

指数平滑法
ARIMA模型

内容：

创建时间序列索引
绘制时间序列图形
处理时间序列数据
建立时间序列模型
模型效果评估
应用模型预测

任务指导

1. 移动平均法

移动平均法（Moving Average）是采用逐项递进的办法，将原时间序列中的若干项数据进行平均，通过平均来消除或减弱时间序列中的不规则变动和其他变动，从而呈现出现象发展变化的长期趋势。

若平均的数据项数为K，就称为K期(项)移动平均。

分为简单移动平均法和加权移动平均法两种。

简单移动平均法将各项数据等同看待，计算每个移动平均值时采用简单算术平均。
加权移动平均法给各期观测值赋予不同的权数，采用加权算术平均来计算每个移动平均值。

移动平均法只能预测一期的数据，预测时通常将移动平均值放在平均时距的最末一期上。

示例：

年份	销售量	两年移动平均		三年移动平均	五年移动平均
1	54	52
2	50	51	51.5	52
3	52	59.5	55.25	56	61
4	67	74.5	67	67	64
5	82	76	75.25	73	72
6	70	79.5	77.75	80	79
7	89	88.5	84	82	83
8	88	86	87.25	87	86
9	84	91	88.5	90	90
10	98	94.5	92.75	91	93
11	91	98.5	96.5	98
12	106

2. 指数平滑法

指数平滑法实际上是一种特殊的加权移动平均法。指数平滑法进一步加强了观察期近期观察值对预测值的作用，对不同时间的观察值所赋予的权数不等，从而加大了近期观察值的权数，使预测值能够迅速反映市场实际的变化。权数之间按等比级数减少，此级数之首项为平滑常数a，公比为(1- a)。

指数平滑法对于观察值所赋予的权数有伸缩性，可以取不同的a 值以改变权数的变化速率。如a取小值，则权数变化较迅速，观察值的新近变化趋势较能迅速反映于指数移动平均值中。

Si=axi+(1-a)Si-1，以此类推。

因此，运用指数平滑法，可以选择不同的a值来调节时间序列观察值的均匀程度(即趋势变化的平稳程度)。

根据平滑次数不同，指数平滑法分为：简单指数平滑法、二次指数平滑法和三次指数平滑法。

简单指数平滑法：也称一次指数平滑法，如果有一个可用相加模型描述的，并且处于恒定水平和没有季节性变动的时间序列，可以使用简单指数平滑法对其进行短期预测。
二次指数平滑法：是对一次指数平滑的基础上再进行平滑，它适用于具线性趋势的时间序列。如果时间序列可以被描述为一个增长或降低趋势的、没有季节性的相加模型则可以使用二次指数平滑法对其进行短期预测。
三次指数平滑法：在二次指数平滑的基础上保留了季节性的信息，使得其可以预测带有季节性的时间序列。

3. ARIMA模型

ARIMA模型为自回归积分移动平均模型，是由博克思(Box)和詹金斯(Jenkins)于70年代初提出一著名时间序列预测方法，所以又称为box-jenkins模型、博克思-詹金斯法。

其中ARIMA（p，d，q），AR是自回归， p为自回归项； MA为移动平均，q为移动平均项数，d为时间序列成为平稳时所做的差分次数。

所谓ARIMA模型，是指将非平稳时间序列转化为平稳时间序列，然后将因变量仅对它的滞后值以及随机误差项的现值和滞后值进行回归所建立的模型。

ARIMA模型根据原序列是否平稳以及回归中所含部分的不同，包括移动平均过程（MA）、自回归过程（AR）、自回归移动平均过程（ARMA）以及ARIMA过程。

一个非平稳时间序列接受了d次差分处理并成为平稳序列时，就能够用一个平稳的ARMA(p,q)模型当作其对应的模型，则称该原始时间序列是一个自回归积分滑动平均时间序列，表示成ARIMA(p,d,q)。

3.1 时间序列的分类

3.2 平稳序列(stationary series)

基本上不存在趋势的序列，各观察值基本上在某个固定的水平上波动；或虽有波动，但并不存在某种规律，而其波动可以看成是随机的。

平稳性时间序列的特点

平稳性要求产生时间序列Y的随机过程的随机特征不随时间变化，则称过程是平稳的；假如该随机过程的随机特征随时间变化，则称过程是非平稳的。
平稳性是由样本时间序列所得到的拟合曲线，在未来的一段期间内能顺着现有的形态能一直地延续下去；如果数据非平稳，则说明样本拟合曲线的形态不具有延续的特点，也就是说拟合出来的曲线将不符合当前曲线的形态。
随机变量Yt的均值和方差均与时间t无关，随机变量Yt和Ys的协方差只与时间差（步长）t-s有关。
对于平稳时间序列在数学上有比较丰富的处理手段，非平稳的时间序列通过差分等手段转化为平稳时间序列处理。

3.3 非平稳序列 (non-stationary series)

有趋势的序列：线性的，非线性的；有趋势、季节性和周期性的复合型序列。

3.4 时间序列的平稳性检验

一般采用三种方法检验：

1）时序图检验

从图中可以看出，很明显的增长趋势，不平稳。

2）自相关系数和偏相关系数

还以上面的序列为例：用SPSS得到自相关和偏相关图。

分析：左边第一个为自相关图（Autocorrelation），第二个偏相关图(Partial Correlation)。

平稳的序列的自相关图和偏相关图要么拖尾，要么是截尾。截尾就是在某阶之后，系数都为 0 。比如上面的偏相关的图，当阶数为1的时候，系数值还是很大为0.914，二阶长的时候突然就变成了0.050.后面的值都很小，认为是趋于0，这种状况就是截尾。什么是拖尾，拖尾就是有一个缓慢衰减的趋势，但是不都为0。

上图中自相关图既不是拖尾也不是截尾。以上的图的自相关是一个三角对称的形式，这种趋势是单调趋势的典型图形，说明这个序列不是平稳序列。

3）单位根检验

单位根检验是指检验序列中是否存在单位根，如果存在单位根就是非平稳时间序列。

3.5 时间序列的差分

ARIMA 模型为平稳时间序列定义的。因此，如果从一个非平稳的时间序列开始，首先需要做时间序列差分直到得到一个平稳时间序列。如果必须对时间序列做 d 阶差分才能得到一个平稳序列，那么就使用ARIMA(p,d,q)模型，其中 d 是差分的阶数。差分，简单来说就是后一时间点的值减去当前时间点，也就是yt-yt-1，每做一次差分就少一个数据。

差分是使时间序列得以平稳的一个很重要的过程，但是差分的阶数选择不对，或者差分的次数过多，反而会丢失太多时间序列的信息。

如果序列存在明显趋势，且呈现近似一条直线的趋势，可对序列作一阶差分，从而消除趋势性；
如果序列存在明显的S期季节性，则可对序列作S阶差分，从而消除季节性。

3.6 ARMA模型的定阶及参数估计

1）在时序数据经过差分（d）变为平稳序列后，可以通过acf和pacf图来判断模型的阶数。

模型	ACF	PACF
AR(p)	拖尾	P阶后截尾
MA(q)	q阶后截尾	拖尾
ARMA(p,q)	q阶后截尾	p阶后截尾

2）使用循环，寻找最优参数

通过循环p和q，循环中建立Arima(p,d,q)模型，通过模型的AIC值来寻找最优模型。

AIC称为赤池信息量准则，是衡量统计模型拟合优良性的一种标准，可以权衡所估计模型的复杂度和此模型拟合数据的优良性。

AIC=2k+nln(SSR/n) k为模型参数个数，n为样本，SSR为残差平方和。

AIC鼓励数据拟合的优良性但是尽量避免出现过度拟合(Overfitting)的情况。所以优先考虑的模型应是AIC值最小的那一个。假设在n个模型中做出选择，可一次算出n个模型的AIC值，并找出最小AIC值相对应的模型作为选择对象。

4. 模型效果评估

衡量一个模型的效果可以通过考察原始值和拟合值之间的残差序列是否近似的为白噪声，说明时间序列中有用的信息已经被提取完毕了，剩下的全是随机扰动,是无法预测和使用的。

白噪声是指一组时间序列中，任意选取两个时间，数据毫不相关的序列。它意味着该时间序列是纯随机的，可以理解为其中没有任何有提取价值的信息。

判断是否白噪声的方法：Ljung-Box test是一种判断序列的自相关函数是否为0的统计方法，是一种白噪声检验法。

模型残差检验：1、残差是否有自相关性；2、残差是否近似服从正态分布；3、残差是否是平稳序列。

5. 完成示例

1）根据公司出货数据（C:\公司出货数据.csv），使用简单移动平均和加权移动平均预测下一期的数据并绘图。

2）根据纪念品商店销售数据（C:\纪念品商店销售数据.csv），分别使用指数平滑法和ARIMA模型进行建立模型，并预测下一年的销售额。

任务实现

1. 移动平均法模型

1）引入相应的库

import pandas as pd
import numpy as np
from statsmodels.tsa import holtwinters as hw
from statsmodels.graphics.tsaplots import plot_acf,plot_pacf
from statsmodels.tsa.stattools import adfuller
from statsmodels.graphics.gofplots import qqplot
import matplotlib.pyplot as plt
from statsmodels.tsa.arima.model import ARIMA
import warnings
warnings.filterwarnings('ignore')

2）读取和处理数据

mydata=pd.read_csv('公司出货数据.csv')
print(mydata.info())

可以看到，数据共144行2列，均为数值型。

print(mydata.head())

print(mydata.tail())

可以看到，date为日期，从2006年1月到2017年12月，tons为出货吨数。

3）建立时间序列索引并绘制时序图

date=pd.period_range('2006/01',periods=len(mydata),freq='M')
tons_data=pd.DataFrame(mydata['tons'].values,index=date,columns=['tons'])
print(tons_data.head())

tons_data.plot()

可以看到，该数据具有趋势的特性，但不存在季节性。2010年之前稳步增长，然后到2012年呈现下降趋势，自2013年以后，一直保持增长的趋势。

4）建立移动平均法模型

建立3年移动平均

tons_data_ma=tons_data.rolling(3).mean()
print(tons_data_ma.head(10))

tons_data['tons_data_ma']=tons_data_ma
tons_data.plot()

当使用跨度为 3 的简单移动平均平滑后，时间序列依然呈现出大量的随便波动。因此，为了更加准确地估计这个趋势部分，也许应该尝试下更大的跨度进行平滑。

正确的跨度往往是在反复试错中获得的。例如，尝试使用跨度为8的简单移动平均：

tons_data_ma=tons_data.drop('tons_data_ma',axis=1).rolling(8).mean()
tons_data['tons_data_ma']=tons_data_ma
tons_data.plot()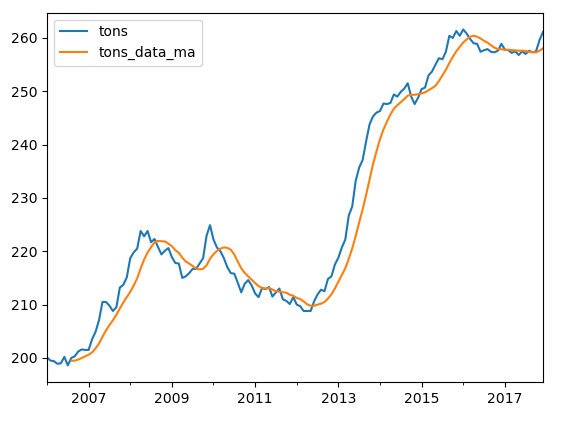

这个跨度为 8 的简单移动平均平滑数据的趋势部分看起来更加清晰了，可以发现这个时间序列前3年是上升，中间4年处于下降趋势，但2013年以后，一直处于上升趋势。

加权移动平均

tons_data.pop('tons_data_ma')
tons_data_ewm=tons_data.ewm(8).mean()
print(tons_data_ewm.head(10))

tons_data['tons_data_ewm']=tons_data_ewm
tons_data.plot()

移动平均就是对时间序列按照权重求均值，因此使用简单。但其最大的缺点是它的滞后性。从图不难看出，随着计算跨度的增大，移动平均线越来越平滑，但同时也越来越滞后。

2. 指数平滑法建立模型

1）读取和处理数据（备注：上一个任务已做）

mydata=pd.read_csv('纪念品商店销售数据.csv')
print(mydata.info())
print(mydata.head())
print(mydata.tail())
date=pd.period_range('1987/01',periods=len(mydata),freq='M')
sales_data=pd.DataFrame(mydata['sales'].values,index=date,columns=['sales'])
print(sales_data.head())
sales_data.plot()
sales_data_log=np.log(sales_data)
sales_data_log.plot()

2）建立指数平滑法模型

hw_model=hw.ExponentialSmoothing(sales_data_log,trend='add',seasonal='add',seasonal_periods=12).fit()
print(hw_model.summary())

summary()既列出三次平滑的α、β、γ值，也列出了各月的季度指数。 α、β、γ的估计值分别是 0.4484,0.00 和 1.043e-17。 α 接近0.5，意味着在当前时间点估计得水平是基于最近观测和历史观测值。 beta 的估计值是 0.00，表明估计出来的趋势部分的斜率在整个时间序列上是不变的，并且应该是等于其初始值。直观的感觉，水平改变非常多，但是趋势部分的斜率 b却仍然是大致相同的。同样gamma 的值（接近0）表明当前时间点的季节性部分的估计基于最近观测值。

3）查看拟合图

sales_data_log.plot()
hw_model.fittedvalues.plot(label='fitted_values',legend=True)

4）模型评估，查看残差

残差自相关图

plot_acf(hw_model.resid)

在残差滞后20阶的自相关图可以看到，自相关系数都在标准范围内，均接近于0，说明残差基本没有自相关性

残差平稳性检验

adfuller(hw_model.resid)

可以看到，通过单位根检验，可以看到p值接近0，不存在单位根，因此可以认为残差序列是平稳的。

残差正态性

plt.figure()
plt.hist(hw_model.resid,density=True)
hw_model.resid.plot(kind='kde')
plt.show()

qqplot(hw_model.resid,line='s')

从直方图、核密度图和正态QQ图可以看到，残差几乎服从正态分布。

5）预测下一年的销售额

sale_forecast1=np.exp(hw_model.predict(start='1994/01',end='1994/12'))
print(sale_forecast1)

绘图

sales_data.plot()
sale_forecast1.plot(label='forecast',legend=True)

3. 建立ARIMA模型

1）差分使数据平稳

log_data_diff1=sales_data_log.diff(12).dropna()   #去除季节性
log_data_diff2=log_data_diff1.diff().dropna()
log_data_diff2.plot()

先做一次滞后12阶的差分，去除季节性的变动，然后做一次差分以消除趋势影响，从图上看数据已经趋于平稳

单位根检验

adfuller(log_data_diff2['sales'])

可以看到，p值接近于0，说明数据已经趋于平稳。

2）通过自相关和偏自相关图定阶（p、q）

plot_acf(log_data_diff2)

plot_pacf(log_data_diff2)

通过acf图，定q=3，通过pacf，定p=1，因此ARIMA模型的参数为ARIMA(1,1,3)

3）通过循环找最优p、q值

index=0
parma_df=pd.DataFrame(columns=['p','d','q','AIC'])
for p in range(6):for q in range(6):        try:myfit=ARIMA(log_data_diff1,order=(p,1,q)).fit()parma_df.loc[index]=[p,1,q,myfit.aic]index+=1except:passmin_param=parma_df.loc[parma_df['AIC'].idxmin()]
print(parma_df)
print('最优的参数为index=%d,p=%d,d=1,q=%d,AIC=%.2f'%(min_param.name,min_param['p'],min_param['q'],min_param['AIC']))

可以看到，最优的p、q值为第3个，p=0，q=3。

4）建立ARIMA模型

arima_model=ARIMA(log_data_diff1,order=(0,1,3)).fit()
print(arima_model.summary())

返回一份格式化的模型报告，包含模型的系数、p值、AIC和BIC等详细指标。

查看拟合图

sales_fittedvalues_log=sales_data_log.shift(12,freq='M')['sales']+arima_model.fittedvalues
sales_data_log.plot()
sales_fittedvalues_log.plot(label='fitted_values',legend=True)

5）模型评估，查看残差