引言
前面讲了很多结构力学,今天来讲讲有关数据分析的内容,后面有机会将会介绍更多相关的内容。数据分析在科学研究和工程应用中非常有用,有时也很好玩。
言归正传,在许多实际问题中,常常需要根据一些已有的数据,实现预测这些数据之外的信息,或解决与这些数据相关的一些问题。
在科学研究和工程计算中最常用的两种方法就是 插值和拟合。
估值函数
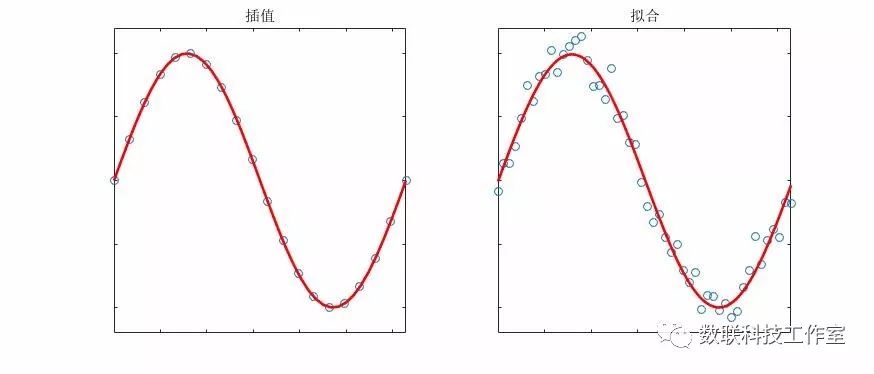
总体来说,两种方法都是通过已有的离散点,在定义域中形成一个 估计函数,在描述已有数据的同时,预测未知数据;该函数可以是显示表达的,也可以是非显示表达的。插值与拟合的区别在于,插值方法需要估计函数严格经过已有数据;拟合方法则允许估计函数和已有数据存在一定误差,从而保证整体最优。
如何插值
在插值过程中,估计函数被称为插值函数,假设F为 插值函数, {g}为 基函数族(有一定要求),a为待定系数,则插值函数可表示为
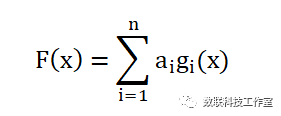
很显然,对于给定N个数据,如果给定了N个基函数g,在一般情况下,待定系数a可以唯一确定;读者可以考虑一下为什么?
估计函数用到的基函数族有很多形式,如多项式和三角函数等,本文主要介绍最常用的多项式形式。
多项式的基函数族通常按幂次由小到达排列,其中通常将g(x)=1视为幂次为0的常数项;通常基函数族都要都要包含常数项;从另一个角度看,基函数族从低频到高频排列,而低频分量总是要优先考虑的。
由以上分析可知,给定N的数据,最多可以确定N-1次多项式。
分段插值
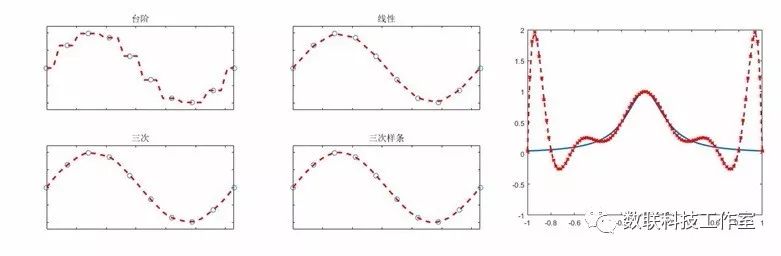
尽管看起来很完美,但使用这种方法,对于一些函数插值可能会引起“震荡”现象,实际上很少采用直接多项式插值。
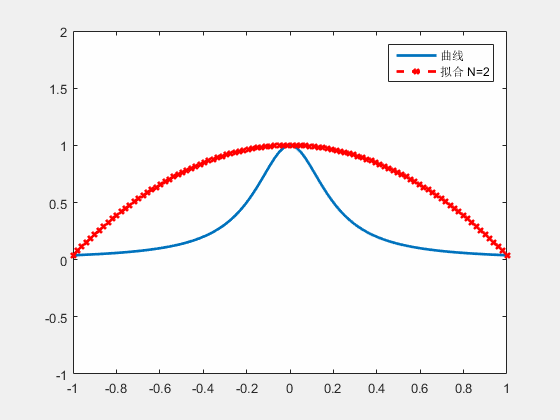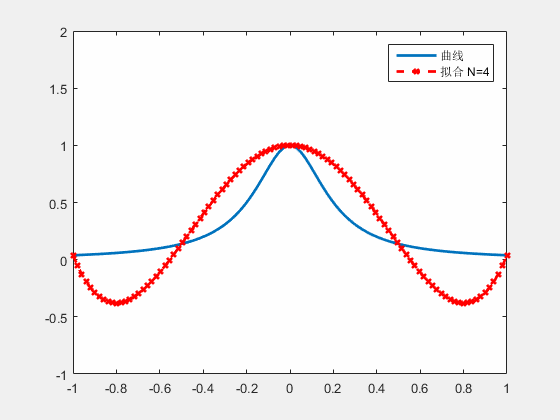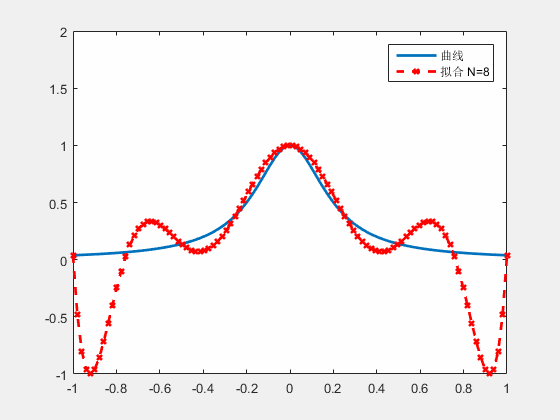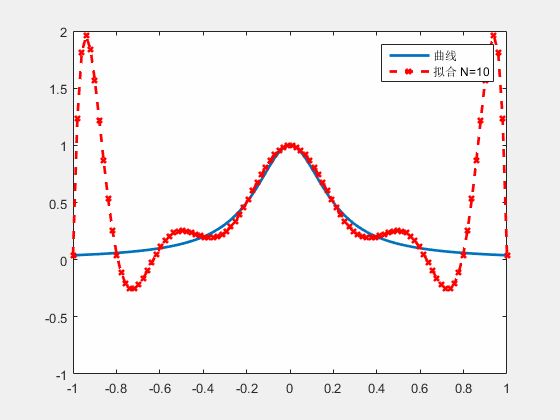
震荡是由高幂次的“高频”函数产生的,我们考虑将横轴划分为多个小段,由一系列低幂次的插值函数组成。
在分段过程中,发现多个低次函数插值会使得分割点出现不连续、不可导等现象。为了解决这个问题,我们在分割点处增加一些约束条件,如连续、可导和多阶可导;带来的代价就是幂次增大。
通常有台阶、线性、三次和 三次样条插值等几种形式;分别对应不连续、不可导、二阶不可导和三阶不可导。由于一般的物理方程都是不高于二阶系统的,因此,三次样条插值是应用非常广泛的一种插值方法。
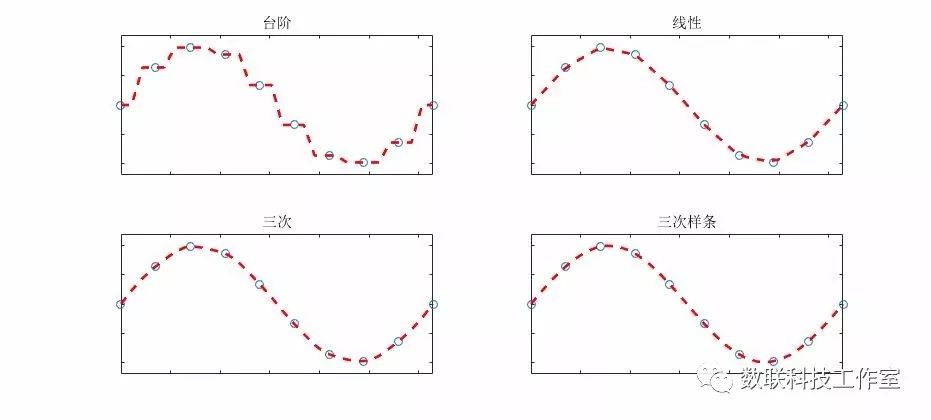
插值的预测
得到插值函数后,可以预测其他未给定的数据;预测值和真实值之间的误差称为插值余项。
拟合
我们把已知数据“最外围”的区域称为边界,在边界内预测称为“内插值”,在边界外预测称为“外插值”;一般而言,内插值能保证良好的精度,而外插值相对不可控,可能会有非常大的误差。因此,如果需要边界处的数据,理论上需要增大数据范围,特别是分段插值,外围的数据通常是不可预测的。后面讲的拟合也有同样的问题。
拟合的方法应用非常广泛,数据处理、参数估计和统计学习等;可以说只要有数据处理的地方,就会用到拟合;当前非常热门的大数据、机器学习和人工智能本质上就是在寻找拟合函数。
拟合的课题太大,本文只简单介绍其基本思想,并探讨应用最广泛的基于 最小二乘的 线性回归,以后文章会有一系列相关的专题开展讨论。
什么是拟合
通过插值方法可以在一定程度上完成预测等任务,但是该方法本身是存在缺陷的。
现实中的数据实际上是包含 误差的,并且当数据量非常大时,插值的结果通常意义不大;此外,对于一些无法用显示函数表达,特别是“结构化”程度较低的数据,插值是无能为力的。考虑对其做一些调整,我们放弃估计函数必须通过已知数据的要求,允许存在一定的误差,同时目标是整体 最优。与插值类似,我们把这里的估计函数称为拟合函数。
这里涉及到两个问题:一是目标函数的选择,二是拟合函数形式的选择。
目标函数
由于拟合函数不需要经过已知数据,因此在已知数据位置,拟合函数的值与给定值存在一个误差,通常目标函数是由数据的误差以及位置组合构成的;更好一点的理解是由“加权”误差组合构造的,而权重则和数据在空间中的位置有关;一般目标函数是我们的求解目标。
这里先不考虑权重,假设每个数据是等价的,最常见的目标函数是由误差距离的和来定义;距离有多种定义方式,如0范数、1范数、2范数和无穷范数等;最常用的是2范数的空间,也就是 欧式空间距离。
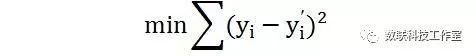
对应的方法即为最小二乘法。
这里多说一句,插值也可以看作是一种特殊的拟合;它要求误差函数在各种目标函数下都是0;当然,插值的实现过程是有一些条件的。
拟合函数的形式
目标函数确定了,接下来讨论拟合函数的形式。
拟合函数的形式有很多,线性、多项式和非线性函数等;甚至可以是一种结构,如树,支持向量机和神经网络等。
这里简单介绍两个概念:
欠拟合:拟合函数的形式相比数据过于简单,不能反映真实情况;
过拟合:拟合函数的形式相比数据过于复杂,“过”反映了真实情况,引入了过多的人为“噪声”和“结构”。
欠拟合:拟合函数的形式相比数据过于简单,不能反映真实情况;
过拟合:拟合函数的形式相比数据过于复杂,“过”反映了真实情况,引入了过多的人为“噪声”和“结构”。
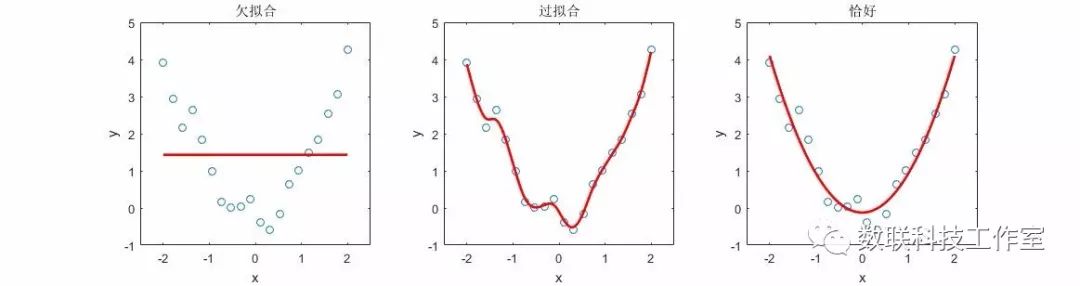
欠拟合相对容易处理,而过拟合则是非常麻烦的问题;可以说在机器学习中,大量的工作都是在解决这个问题。
这里要提一下“奥卡姆剃刀”原理,说的是“如无必要”,“勿增实体”;它的意思是,如果能用简单的表达式,就不应该用更复杂的来替代,应该尽量把多余的去除。在拟合中就是要求我们尽可能用简单的方式描述问题,避免过拟合的情况出现。
基于最小二乘的线性回归
本文介绍最简单,并且应用最广泛的最小二乘线性回归;在这类问题中,拟合也称为回归。
将拟合的函数假设为
这个线性函数可以是直线、平面或者超平面,对应变量和系数的维度不同。
这里可以用两种视角看:
把系数看成未知,数据看成已知,要使目标函数最小,可通过求解函数极值问题的方法,对系数求导形成线性方程组求解;
把假设的线性函数看成函数空间,要使目标函数最小,可通过求解泛函极值问题的方法,用变分法形成线性方程组求解;
二者等价。
把系数看成未知,数据看成已知,要使目标函数最小,可通过求解函数极值问题的方法,对系数求导形成线性方程组求解;
把假设的线性函数看成函数空间,要使目标函数最小,可通过求解泛函极值问题的方法,用变分法形成线性方程组求解;
二者等价。
此外,还能证明当误差符合高斯分布时,最小二乘法和极大似然估计是等价的;也就是说最小二乘法实际上假定了误差分布符合高斯分布;具体证明网上都可以找到,以后有机会也可以讲讲。
机器学习
在机器学习中,为了验证拟合函数的“ 泛化”性能,同时优化参数以及调整超参数;并不像传统的学科,把所有已知数据全用作拟合函数用;而是将其分割为训练集、验证集和测试集等,开展优化及评估。
“分类”在机器学习中是一类典型的问题,也可通过拟合的方式实现。此外,为了避免过拟合,大量的“ 正则化”方法应用其中。
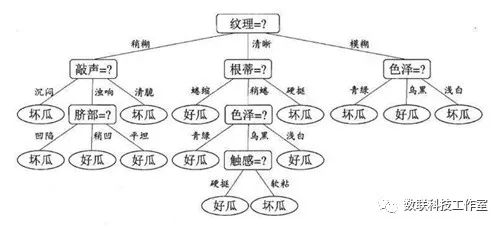
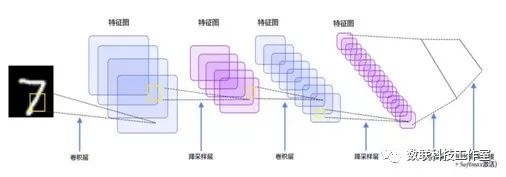
其他应用
拟合的方法不仅可以预测数据,针对不同问题还可以有多种其他应用。
比如采集的数据理想状态是一个平面或者曲面,但实际上存在一定误差;可以通过拟合,先形成理想平面或者曲面,再计算RMS和偏离度等,评估其误差以及离散度。
作者:数联科技工作室
声明:首发数联科技工作室公众号(ID:DigitUnionTecHouse),部分图片源自网络,如有不当请联系我们,欢迎分享。
如果您正在学习CAE,欢迎加入我们的学习型工程师社群,与我们抱团一起学习理论、软件和行业应用。更多详情请咨询仿真小助手(在仿真秀公众号对话框回复小助手,备注进群即可)


















