天津新东方的老师们今天要带大家了解一下——牛顿第二定律的应用之整体法公式;传送带模型;板块模型;瞬时加速度问题。
(一)牛顿第二定律的应用之基础篇
高中物理作为物理学的基础引入部分,主要针对相互作用和物质运动规律的研究展开学习。而建立相互作用和物体运动的桥梁的就是我们必修一课本里的牛顿三大定律。而其中对于牛顿第二运动定律的考察属于高考中的重点,其对力和运动的研究方法更是贯穿高中三年的物理学习。所以本文我们主要针对牛顿第二运动定律的理解和运用进行简单剖析。
首先我们先来看课本上牛二律的表述:物体的加速度的大小跟它受到的作用力成正比、跟它的质量成反比,加速度的方向跟作用力的方向相同。用公式来表示解释F合=ma,亦即它点明了受力情况与运动情况的关系。所以我们可以通过受力决定运动情况,也可以从运动情况分析受力。
本篇首先说下动力学两类基本问题的分析程序
一、从物体的受力情况确定运动情况
1.确定研究对象,对研究对象进行受力分析
2.根据力的合成和分解求出物体所受的合力
3.根据牛顿第二定律求出物体的加速度
4.结合物体运动初始条件,根据匀变公式求出所需运动参量
例题:一个静止在动摩擦因数的因数为0.5粗糙水平面上的物体,质量为2kg,在16N的水平拉力作用下开始运动,那么物体在4s末的速度和4s内的位移怎么求呢?
分析:首先我们分析物体水平方向的受力有16N的拉力和10N的摩擦力,然后再根据力的合成和分解的方法可以计算出合力为6N,再根据牛顿第二定律可以计算得出物体运动的加速度为3m/s2,再根据匀变的的运动规律公式继而可以求出我们要求的问题。
二、从物体的受力情况确定运动情况
1.确定研究对象,对研究对象进行受力分析
2.根据运动学公式求出加速度
3.根据牛顿第二定律求出物体的合力
4.根据力的合成与分解的方法,由合力和已知力求出未知力。
这一块我们可以从失重超重的典例分析来看。人的质量为m,当电梯启动向上加速时,根据牛顿第二定律可知,人的合力方向向上等于ma。然后再分析人的受力情况:向下的重力和向上的支持力,所以可以判断出支持力大于重力。所以我们判断物体失重或超重是需要判断物体加速度的方向即可。当物体加速度向下是为失重状态,物体加速度向上是为超重状态。
(二)牛顿第二定律的应用之整体法公式
上篇我们简单地介绍了牛顿第二定律的基本内容和及分析方法,接下来我们主要针对牛二律的各类进阶模型进行细致的分类分析。首先我们先来介绍整体法的牛顿第二定律公式。
我们之前在进行静力学分析时,会学到过整体隔离法。当时在处理连接体问题或多个物体时其分析方法是忽略掉系统内部的相互作用力,只分析整体受到的满足平衡条件的外力来解决问题。那么我们现在可以尝试下先用基本的动力学处理方法对下面的例题进行分析。
一质量为m的物体,在粗糙斜面上自静止滑下,问地面对斜面体的力的作用情况。
1.分析斜面体受力:自身的重力、地面给的支持力、以及物体给的压力和摩擦力和可能存在的地面给的摩擦力。
2.斜面运动情况:加速度为0。
3.根据平衡条件容易判断出物体受地面向左的摩擦力,且通过计算可得(详解见图)地面给的支持力小于物体加斜面体的重力。
接下来我们可以尝试忽略掉物块和斜面体的相互作用力,亦即整体受总重力+支持力+摩擦力,通过力的合成和分解可以求得整体的合外力。
这个时候我们发现一个有趣的事是整体法求得的合力刚好等于物块的合力,所以我们得出一个规律:F合=m1a1+m2a2+........,整体的合力等于系统内部各个个体受到的合力之和。所以如果用这个规律来处理这个问题就会变得简单许多,我们不需要考虑复杂的力的合成计算,我们只需要分析物块有左下的加速度以及斜面体静止,就可以分析出整体有一个沿左下的合力,基于此便很容易判断出整体有一个地面给的向左的摩擦力,且地面给的支持力要小于总重力。
接下来我们可以通过对连接体的模型的分析来实践一下我们的牛二律的整体法公式。
对于连接体模型会有两种情况,一是系统内部的物体具有相同的加速度,另外当然就是系统内部的物体具有不同的加速度。
前者常见的模型就是我们的由绳子连接的情况,如图1所示,因为两个物体的加速度相同,所以用整体法很轻松就可以算出F-(M+m)g=(M+m)a。
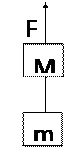
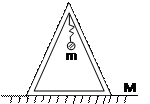
至于加速度不同的情况我们只需要分开讨论各自的加速度代入公式计算就可以。比如下面这道例题:质量为M的框架放在水平地面上,一轻弹簧上端固定在框架上,下端固定一个质量为m的小球。小球上下振动时,框架始终没有跳起,当框架对地面压力为零瞬间,此时进行整体的受力分析:只有重力(M+m)g,根据牛二律整体法公式:F合=ma+M*0可以算出m的加速度为(M+m)g/m。
(三)牛顿第二定律的应用之传送带模型
上篇我们介绍了牛二律的整体法应用,今天我们来看下在高考中经常出现的传送带模型的分析方法。
处理这类问题肯定还是需要将力与运动结合起来去分析,那么在传动带中我们主要分析的其实只有物体与传送带之间的摩擦力。所以我们的分析流程可以总结为以下步骤:
1.根据物块与传送带的运动情况确定相对运动速度大小及方向
2.根据相对运动方向确定摩擦力的性质
3.根据摩擦力的性质确定合力继而得到加速度大小方向
4.根据加速度判断物体运动情况
5.根据物体运动情况判断是否可以共速
6.若可共速则还需判断共速后是否发生相对运动的变化继而引起摩擦力的变化
下面我们通过两道例题来进行分析

如图所示为水平传送带装置示意图,绷紧的传送带AB始终保持v0=2 m/s的恒定速率运行,一质量为m的工件无初速度地放在A处,传送带对工件的滑动摩擦力使工件开始做匀加速直线运动,设工件与传送带间的动摩擦因数为μ=0.2 ,AB的之间距离为L=10m ,g取10m/s2 .求工件从A处运动到B处所用的时间。
首先我们确定物块相对于传送带向左运动,所以物体受传送带向右的摩擦力,继而根据牛二律可以求得物块的加速度为2m/s2,则物块达到与传送带共速需要经过1s的时间且走过1m,小于AB间的距离L。所以物块再与传送带共速后还会以2m/s的继续前进9m,也就是还需要4.5s才能到达B端。这里边我们会看到在与传送带共速之后物块的受力情况会发生变化,进而引起运动情况的变化,这是我们在分析此类问题时尤其需要注意的地方。
但注意共速之后一定会导致摩擦力的消失么,其实,下面我们可以来这道斜面传送带的问题。如图所示,传送带与水平方向夹37°角,AB长为L=16m的传送带以恒定速度v=10m/s运动,在传送带上端A处无初速释放质量为m=0.5kg的物块,物块与带面间的动摩擦因数μ=0.5,求:当传送带逆时针转动时,物块从A到B所经历的时间为多少?

在这道题的分析中我们可以发现AB在以10m/s2的加速度加速一秒后与传送带共速,但之后并不会与传送带共速,摩擦力只是由向下变成向上,加速度变为2m/s2,所以我们需要分析两段运动来解题。总结一下来说除了常规的力学分析情况,我们还需要额外注意的是传送带长度是否可以满足共速所需位移,以及共速之后摩擦力的变化情况。
(四)牛顿第二定律的应用之板块模型
上篇我们针对传送带模型进行简单分析,这篇我们来说一下板块模型的问题。实际上板块模型涉及到各类比较复杂的问题,包括之后的动量能量相关的问题之类,但这里我们只对板块模型的运动情况进行简单剖析。
其实板块模型和传送带问题是很像的一个问题,只不过后者的分析是从传送带与物体之间的相对运动来判断受力情况再决定运动,而板块模型却面临一个是否存在相对滑动这一运动情况的判断。那么这里其实我们就需要用到最大静摩擦力的概念了:fmax是物体将要发生相对运动这一临界状态时的摩擦力。所以在判断板块模型是否能发生能共速时,我们会将此作为主要判断依据,或者以此来求相关临界状态问题。
例题:我们可以来分析下面这道题:如图1所示,光滑水平面上放置质量分别为m、2m的物块A和木板B,A、B间的最大静摩擦力为μmg,现用水平拉力F拉B,使A、B以同一加速度运动,求拉力F的最大值。
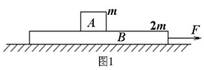
分析:题目要求A、B共速时拉力F最大值。既然共速,属于我们之前提过的共加速的连接体问题,所以采用整体法a=F/(2m+m)。而发生相对滑动的临界情况是A、B之间的摩擦力等于最大静摩擦力,此时A的加速度为A的最大加速度=μmg/m=μg,此时F=3mμg,即拉力F的最大值。
所以我们可以借此来确定物块的详细运动情况,进而借助匀变运动学规律也就可以很方便地解决涉及到一些比如求相对位移和恰好不掉落等等的问题了,接下来我们通过一道综合性例题来了解一下。
例题:如图(a)所示,在足够长的光滑水平面上,放置一长为L=1m、质量为m1=
0.5kg的木板A,一质量为m2=1kg的小物体B以初速度v0滑上A的上表面的同时对A施加一个水平向右的力F,A与B之间的动摩擦因数为μ=0.2,g=10m/s2;小物体B在A上运动的路程S与F力的关系如图(b)所示。求:v0、F1、F2。
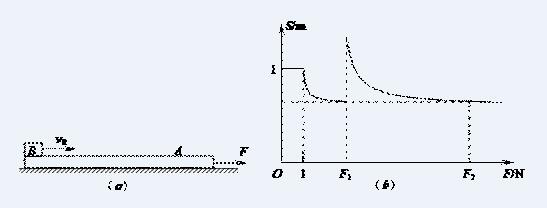
分析:在外力比较小时,板块时可以达到共速的,但此时相对位移刚好等于板长意味着物体会从板的右端滑下所以这时限制相对位移的就是板的长度,所以当F=1N时,板块刚好在相对位移为1m时共速,所以借助运动学公式可以分别求出板块的位移,其差值为1m,借此即可求出题目要求的初速度v0=4m/s。而随着F的增加至大于发生相对滑动时的最大外力即F1=3N之后,板块在达到共速之后,物块会相对木板向左运动,所以这种情况下物块在木板上先向右运动再从左边滑下,需要考虑两段相对位移。
(五)牛顿第二定律的应用之瞬时加速度问题
这篇我们主要进行瞬时加速度问题的分析。瞬时加速度问题实质上是对牛顿第二定律的瞬时性的考察。总结解决方法如下:
1.首先分析变化前的物体的受力情况
2.判断状态变化引起的受力变化
3.根据变化后的受力结合牛顿第二定律求解加速度
在这三个步骤中其实最关键的是分析物体受力变化,这里我们主要分为两种情况
1.弹簧模型:弹簧的受力主要看形变量,而其形变恢复不可能瞬时完成,所以在瞬时问题上认为弹力大小不变。
2.绳杆+接触面模型:这三类情况引起弹力的弹性形变都是微小形变,认为不需要形变恢复时间,所以在瞬时问题上这类弹力是可以突变的。
接下来我们从几道例题分别来看下相关问题。
例题:如图所示,一质量为m的物体系于长度分别为L1、L2的两根细线上,L1的一端悬挂在天花板上,与竖直方向夹角为θ,L2水平拉直,物体处于平衡状态。现将L2线剪断,求剪断瞬时物体的加速度?
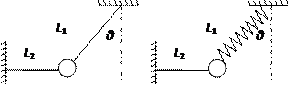
分析:1.首先分析剪短前的受力:重力和沿绳的两个拉力F1、F2;
2.剪短L2后的受力:重力不变、F2变为0,F1由mg/cosθ变为mgcosθ(剪短L2后,L1绳长不会伸长,所以瞬时加速度方向应垂直于L1)
3.根据牛二律可以算出瞬时加速度为gsinθ
总结:这里面我们需要注意的是除了被剪断的L2绳子的拉力变为0,因为绳子不可伸长的特性导致L1绳子中的弹力也发生了突变。
例题:那如果将图(a)中的细线L1改为长度相同、质量不计的轻弹簧,如图5(b)所示,其他条件不变,求剪断瞬时物体的加速度?
分析:对于这种情况因为剪短前后弹簧的弹力不会发生变化,所以很容易判断出剪短后物体的合力向左等于mg/tanθ
那么对于接触面的弹力瞬时变化,我们需要从整体法进行分析,视存在相互作用力的两个物体为一个整体分析受力情况继而得出运动情况
例题:如图14所示,吊篮A、物体B、物体C的质量相等,弹簧质量不计,B和C分别固定在弹簧两端,放在吊篮的水平底板上静止不动。将悬挂吊篮的轻绳剪断的瞬间,各物体加速度怎么分析?
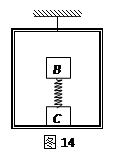
分析:首先分析B的受力:重力和弹簧弹力都不会变化所以瞬时加速度为0;
对于C和A:剪短绳子之后两个共速,需要分析整体受力,弹力和重力不变,绳子拉力变为0,所以加速度为3g/2,此时我们可以发现A、C之间的弹力由2mg变为0.5mg。

- 编辑:天津新东方全科教育-杨仲祥
- 审核:attis
- 声明:新东方编辑人员原创内容,转载请注明出处!