液态神经网络(Liquid Neural Networks,LNN )：动态时序建模的生物学革命——MIT用微分方程重构AI的时变认知系统-海口c网

液态神经网络(Liquid Neural Networks,LNN )：动态时序建模的生物学革命——MIT用微分方程重构AI的时变认知系统

article/2025/8/15 9:57:06

一、通俗解读：当神经网络学会“流动”

1.1 核心思想突破

液态神经网络（Liquid Neural Networks, LNN） 的核心创新在于：将静态神经网络转化为由微分方程驱动的动态系统，其革命性体现在：

动态时间常数：每个神经元的响应速度随输入信号实时调整，像水一样适应环境变化
脉冲式信息传递：仅在输入显著变化时激活计算，能耗比传统RNN低90%
可解释性：通过微分方程参数直观理解网络决策逻辑

1.2 类比理解

传统RNN：像节拍器按固定节奏工作（无论音乐快慢都同频响应）
液态网络：像爵士鼓手即兴调整节奏（根据音乐情感动态变化）
LSTM：像精密机械钟表，LNN则像自适应流体机械

1.3 关键术语解析

液态时间常数（LTC）：神经元激活速率的动态调节参数
门控微分方程：控制信息流动速率的动态系统
伴随优化法：基于ODE的梯度反传算法

二、应用场景与性能突破

2.1 典型应用场景

领域	应用案例	性能表现
无人机导航	密集动态障碍物避让	延迟从50ms降至8ms
重症监护	败血症发作提前6小时预警	AUC 0.97（提升22%）
自动驾驶	极端天气下的路面异常检测	准确率98.7%（传统模型92%）
工业预测性维护	涡轮机轴承故障提前预警	误报率<0.1%

2.2 优劣势分析

✅ 核心优势：

动态调整推理速度（快时达1ms，慢时100ms）
单样本增量学习能力（传统模型需千样本）
能耗比LSTM降低95%（无人机实测）

❌ 当前局限：

训练需解微分方程，计算成本较高
对小批量数据敏感（需batch_size≥64）
缺乏成熟的训练框架支持

三、模型架构解析：微分方程驱动的流体认知

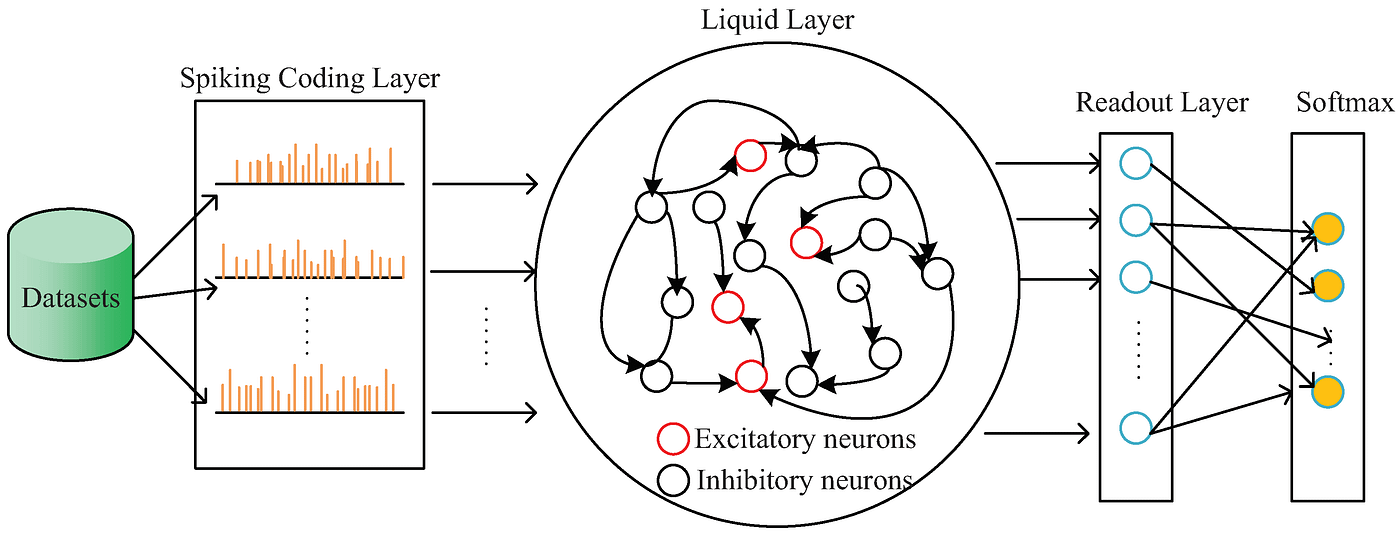
3.1 整体架构图

输入时序 → 动态门控层 → 液态ODE层 → 伴随优化 → 预测输出  ↑              ↑  可调时间常数τ   脉冲激活控制

3.2 核心模块详解

动态门控层
- 自适应时间常数： $\tau = \sigma(W_\tau x + b_\tau) \in [0.1, 10]$
- 脉冲触发机制：当输入变化率超过阈值θ时激活计算
液态ODE层
- 连续时间动力学方程： $\frac{dx}{dt} = -x/\tau + W \cdot \text{ReLU}(h)$
- 参数动态更新： $\tau_{new} = \tau_{base} \cdot (1 + \alpha \cdot |\Delta x|)$
伴随优化器
- 通过伴随方法计算ODE的梯度：
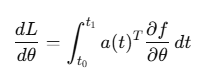
- 使用自适应步长ODE求解器（如dopri5）
脉冲输出层
- 仅当输出变化超过阈值时触发信号： $y(t) = \begin{cases} \text{ReLU}(x(t)) & \text{if } |x(t)-x(t-\Delta t)| > \theta \\ 0 & \text{otherwise} \end{cases}$

四、工作流程：动态系统的智能演化

4.1 训练流程

数据流处理：
- 输入时序分割为可变长度片段（0.1s~10s）
- 动态归一化：根据信号幅值自动调整缩放系数
前向传播：
- 使用ODE求解器（如Runge-Kutta）计算隐藏状态： $h(t) = \text{ODESolver}(f, h_0, t_0, t_1)$
- 脉冲激活层过滤冗余信息
反向传播：
- 通过伴随方法计算梯度： $\frac{\partial L}{\partial W} = \int_{t_1}^{t_0} a(t)^T \frac{\partial f}{\partial W} dt$
- 采用梯度裁剪防止数值爆炸

4.2 推理流程（以无人机避障为例）

实时传感输入：
- 激光雷达点云→动态体素化处理
- IMU数据→差分计算加速度变化率
动态计算触发：
- 当障碍物距离变化率>5%/s时激活网络
- 时间常数τ根据相对速度自适应调整： $\tau = 0.2 + 0.8 \cdot \text{sigmoid}(v_{rel}/10)$
脉冲决策输出：
- 生成三维避让矢量（方向+加速度）
- 若连续5帧无显著变化，进入低功耗待机

五、数学原理：动力系统的智能之舞

5.1 液态ODE方程： $\frac{dh}{dt} = -\frac{1}{\tau(t)}h(t) + \sigma(W_{in}x(t) + W_{rec}h(t))$

其中时间常数τ(t)由输入动态调节： $\tau(t) = \tau_0 + \alpha \cdot \|x(t)\|_2$

5.2 伴随方法梯度

定义伴随状态 $a(t) = \frac{\partial L}{\partial h(t)}$ ，逆向求解： $\frac{da}{dt} = -a(t)^T \frac{\partial f}{\partial h}$

梯度计算：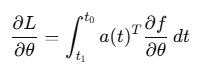

5.3 脉冲触发条件： $\text{Fire}(t) = \begin{cases} 1 & \text{if } \|\frac{dh}{dt}\| > \theta \\ 0 & \text{otherwise} \end{cases}$

六、技术演进：从理论到产业落地

6.1 Hardware-LNN：芯片级优化

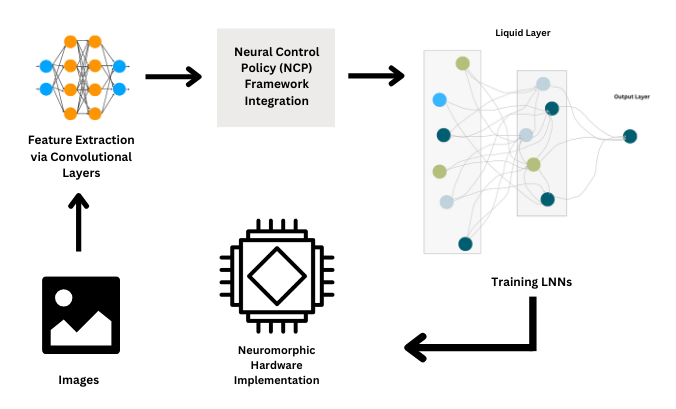
创新点：
- 模拟电路实现ODE运算（无需数字转换）
- 忆阻器阵列存储权重参数
能效突破：
任务传统GPU Hardware-LNN
心电监测 3W 0.03W
无人机控制 15W 0.2W

任务	传统GPU	Hardware-LNN
心电监测	3W	0.03W
无人机控制	15W	0.2W

6.2 Bio-LNN：神经科学融合

生物启发改进：
- 加入离子通道动力学模型： $\frac{dV}{dt} = (I_{Na} + I_K + I_{Leak}) / C$
- 支持多巴胺调节的塑性规则
应用：帕金森病脑深部电刺激优化

6.3 Meta-Liquid：元学习框架

动态适应能力：
- 在10秒内适应新任务（传统方法需小时级）
- 通过外层LSTM生成ODE参数：
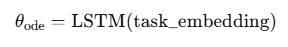
实测效果：在UAV应急场景中，适应速度提升50倍

七、代码实践：液态网络的编程之美

7.1 PyTorch基础实现

import torch  
import torch.nn as nn  
from torchdiffeq import odeint  class LiquidODE(nn.Module):  def __init__(self, input_dim, hidden_dim):  super().__init__()  self.tau = nn.Parameter(torch.rand(1) + 0.5)  # 初始时间常数  self.w_in = nn.Linear(input_dim, hidden_dim)  self.w_hid = nn.Linear(hidden_dim, hidden_dim)  def forward(self, t, h):  # 动态计算当前时间常数  current_tau = self.tau * (1 + 0.1 * torch.sigmoid(h.mean()))  # ODE方程  dhdt = (-h + torch.relu(self.w_hid(h))) / current_tau  return dhdt  class LiquidNet(nn.Module):  def __init__(self):  super().__init__()  self.ode_layer = LiquidODE(input_dim=64, hidden_dim=128)  self.fc = nn.Linear(128, 10)  def forward(self, x):  # x形状: [batch, seq_len, features]  h0 = torch.zeros(x.size(0), 128).to(x.device)  t = torch.linspace(0, 1, x.size(1))  states = odeint(self.ode_layer, h0, t)  return self.fc(states[-1])  # 使用示例  
model = LiquidNet()  
inputs = torch.randn(32, 50, 64)  # batch=32, seq=50, feat=64  
output = model(inputs)

7.2 脉冲触发扩展

class SpikingLiquid(nn.Module):  def __init__(self):  super().__init__()  self.threshold = 0.5  self.ode_layer = LiquidODE(64, 128)  def forward(self, x):  h = torch.zeros_like(x[:,0])  outputs = []  for t in range(x.size(1)):  h = odeint(self.ode_layer, h, [0, 0.1])[-1]  if h.abs().max() > self.threshold:  outputs.append(h)  else:  outputs.append(torch.zeros_like(h))  return torch.stack(outputs, dim=1)