二叉查找树 —— 最近公共祖先问题解析（Leetcode 235）-海口c网

二叉查找树 —— 最近公共祖先问题解析（Leetcode 235）

article/2025/6/19 4:51:03

🏠个人主页：尘觉主页

文章目录

二叉查找树 —— 最近公共祖先问题解析（Leetcode 235）
- 🧠 问题理解
- - 二叉查找树（BST）特点回顾：
- 💡 解题思路
- 🔍 图示解析
- ✅ Java 实现
- - 🚀 时间复杂度分析：
- 📝 总结

二叉查找树 —— 最近公共祖先问题解析（Leetcode 235）

在树结构中，寻找**两个节点的最近公共祖先（Lowest Common Ancestor, LCA）是一个常见的面试题目。而当这道题目出现在二叉查找树（BST）**中时，问题便可以更加高效地解决。

本文将结合 Leetcode 第 235 题 Lowest Common Ancestor of a Binary Search Tree，讲解 BST 中如何快速找出两个节点的最近公共祖先，并配以图示和代码解析。

🧠 问题理解

题目要求：
给定一棵二叉查找树（BST）和树中的两个节点 p 和 q，找出它们的最近公共祖先节点。

二叉查找树（BST）特点回顾：

对于任意一个节点 root：
- 左子树上所有节点的值都小于 root.val
- 右子树上所有节点的值都大于 root.val

💡 解题思路

因为是 二叉查找树，我们可以利用其有序性来减少不必要的搜索，找到一个“分叉点”，这个点正是两个节点 p 和 q 的最近公共祖先。

具体判断逻辑如下：

如果当前节点 root.val 大于 p.val 和 q.val，说明 p 和 q 都在左子树中，继续在左子树递归查找；
如果当前节点 root.val 小于 p.val 和 q.val，说明 p 和 q 都在右子树中，继续在右子树递归查找；
如果 root.val 介于 p.val 和 q.val 之间（即一个在左子树、一个在右子树，或者其中一个就是 root），那么 root 就是最近公共祖先。

📌 注意：为了避免顺序混乱，我们通常在判断前使用 p 和 q 中的较小值、较大值进行比较。

🔍 图示解析

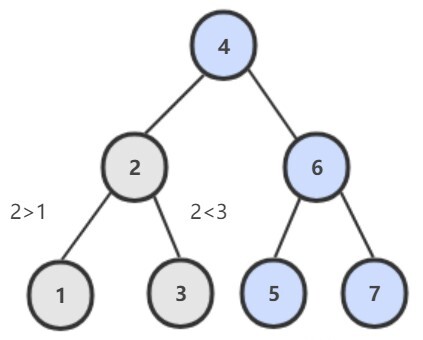
如图所示，在一个典型的 BST 中，若 p = 2，q = 8，那么 6 是它们的最近公共祖先，因为从根节点 6 出发，p 在左子树，q 在右子树。

✅ Java 实现

public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {if (root == null) return root;if (root.val > p.val && root.val > q.val)return lowestCommonAncestor(root.left, p, q);if (root.val < p.val && root.val < q.val)return lowestCommonAncestor(root.right, p, q);return root;
}