《圆柱与圆锥》知识点
圆柱知识点
圆柱的相关计算公式:
底面积 :S底=πr²
底面周长:C底=πd=2πr
侧面积 :S侧=2πrh
表面积 :S表=2S底+S侧=2πr²+2πrh
体积 :V柱=πr²h
圆柱的切割:
①横切:切面是圆,表面积增加2倍底面积,即S 增 =2πr²
②竖切(过直径):切面是长方形(如果h=2R,切面为正方形),该长方形的长是圆柱的高,宽是圆柱的底面直径,表面积增加两个长方形的面积,即S增=4rh
圆柱的特征:
①底面的特征:圆柱的底面是完全相等的两个圆。
②侧面的特征:圆柱的侧面是一个曲面。
③高的特征 :圆柱有无数条高。
圆柱的侧面展开图:
①沿着高展开,展开图形是长方形,如果h=2πr,则展开图形为正方形
②不沿着高展开,展开图形是平行四边形或不规则图形
③无论怎么展开都得不到梯形
圆锥知识点
圆锥的相关计算公式:
底面积:S底=πr²
底面周长:C底=πd=2πr
体积:V锥=1/3πr²h
圆锥的切割:
①横切:切面是圆
②竖切(过顶点和直径直径):切面是等腰三角形,该等腰三角形的高是圆锥的高,底是圆锥的底面直径,面积增加两个等腰三角形的面积,即S增=2rh
圆锥的特征:
①底面的特征:圆锥的底面一个圆。
②侧面的特征:圆锥的侧面是一个曲面。
③高的特征:圆锥有一条高。
圆柱和圆锥的关系
①圆柱与圆锥等底等高,圆柱的体积是圆锥的3倍。
②圆柱与圆锥等底等体积,圆锥的高是圆柱的3倍。
③圆柱与圆锥等高等体积,圆锥的底面积(注意:是底面积而不是底面半径)是圆柱的3倍。
④圆柱与圆锥等底等高 ,体积相差2/3Sh
《圆锥的体积》应用题专项练习
1、求下面圆锥的体积。(单位:厘米)
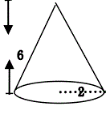
体积:1/3×3.14×2×2×6=25.12(立方厘米)
2、求下图的体积(单位:厘米)
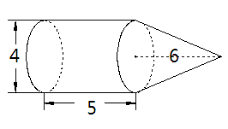
底面半径:4÷2=2(厘米)
体积:3.14×2×2×5+3.14×2×2×6÷3=87.92(立方厘米)
3、一个圆锥的体积是126立方厘米,底面积是42平方厘米,高是多少厘米?
高=体积×3÷底面积126×3÷42=9(厘米)
4、等底等高的圆柱和圆锥的体积的和是96立方分米,圆柱和圆锥的体积分别是多少立方分米?
等底等高的圆柱和圆锥的体积比为3:1
按比例分配:96÷(3+1)=24(立方分米)
圆柱体积:24×3=72(立方分米)
圆锥体积:24×1=24(立方分米)
5、等底等高的圆柱和圆锥,圆柱的体积比圆锥的体积多24立方分米,圆柱和圆锥的体积分别是多少立方分米?
等底等高的圆柱和圆锥的体积比为3:1
按比例分配:24÷(3-1)=12(立方分米)
圆柱体积:12×3=36(立方分米)
圆锥体积:12×1=12(立方分米)
6、一个圆锥形麦堆,底面半径是3米,高是5米,每立方米小麦约重700千克,这堆小麦大约有多少千克?
体积:1/3×3.14×3×3×5=47.1(立方米)
重量:47.1×700=32970(千克)
7、一个圆锥形谷堆,绕着谷堆的外围走一圈是25.12米,高3米,每立方米谷重1.5吨,这堆谷共重多少吨?
底面半径:25.12÷3.14÷2=4(米)
体积:3.14×4×4×3÷3=50.24(立方米)
重量:50.24×1.5=75.36(吨)
8、有一个圆锥体沙堆,底面积是3.6平方米,高2.5米。将这些沙铺在一个长4米,宽2米的长方体沙坑里,能铺多厚?
体积不变
圆锥体积=1/3×3.6×2.5=3(立方米)
厚:3÷4÷2=0.375米
9、一个圆锥形的稻谷堆, 底面周长12.56米, 高1.5米, 把这堆稻谷装进一个圆柱形粮仓, 正好装满.这个粮仓里面的底直径为2米, 高是多少米?
稻谷的体积不变
圆锥的底面半径:12.56÷3.14÷2=2(米)
圆柱的半径:2÷2=1(米)
圆锥的体积:1/3×3.14×2×2×1.5=6.28(立方米)
圆柱的底面积:3.14×1×1=3.14(平方米)
圆柱的高:6.28÷3.14=2(米)
10、一个圆锥形沙堆,底面周长是18.84米,高2.8米。用这堆沙在10米宽的公路上铺4厘米厚的路面能够铺多少米?
体积不变
圆锥的底面半径:18.84÷3.14÷2=3(米)
圆锥的体积:3.14×3×3×2.8÷3=26.376(立方米)
路面的厚度:26.376÷10÷(4÷100)=65.94(米)
11、一个底面直径是12cm的圆锥形木块,把它分成形状大小完全相同的两个木块后,表面积比原来增加了120cm2,这个圆锥形木块的体积是多少?
增加的面积是两个三角形
一个三角形的面积:120÷2=60(平方厘米)
高:60×2÷12=10(厘米)半径:12÷2=6(厘米)
体积 : 1/3×3.14×6×6×10=376.8(立方厘米)
来源:网络