坚硬的盐层上呈现非常一致的不规则图案

过去一个世纪，上图里的旧金山海湾盐沼一直被用来进行工业盐生产。下图显示的是位于玻利维亚南部的世界最大盐沼——天空之镜(Salar de Uyuni)。坚硬的盐层上呈现非常一致的不规则图案，这是典型的分形。

3.菊石缝线

菊石缝线

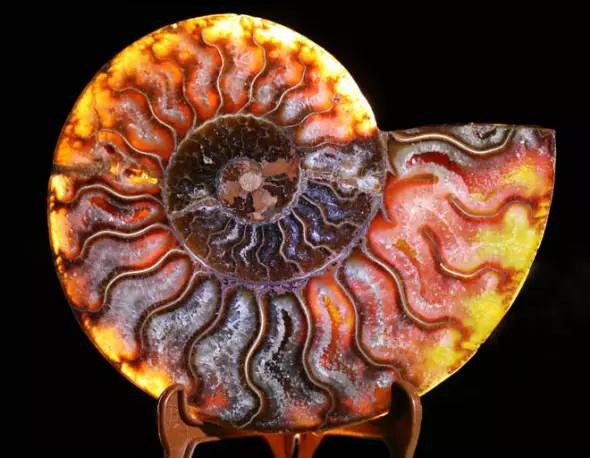
大约6500万年前灭绝的菊石

在大约6500万年前灭绝的菊石，是制作分成许多间隔的螺旋形外壳的海洋头足纲动物。这些间隔之间的壳壁被称作缝线，它是分形复曲线。美国著名古生物学家史蒂芬·杰伊·古尔德依据不同时期的菊石缝线的复杂性得出结论说，进化并没驱使它们变得更加复杂，我们人类显然是“一个例外”，是宇宙里独一无二的。菊石的外壳还生长成一个对数螺旋型，很显然，自然界经常会出现这种图案，例如罗马花椰菜。

4.山脉

山脉

山脉是构造作用力和侵蚀作用的共同产物，构造作用力促使地壳隆起，侵蚀作用导致一些地壳下陷。这些因素共同作用的产物，是一个分形。上图显示的是喜马拉雅山脉，它是世界很多最高峰的所在地。印度板块和欧亚板块在大约7000万年前相撞在一起，导致喜马拉雅山脉隆起，现在这座山脉的高度仍在不断增加。

5.蕨类植物

蕨类植物是一种常见的自相似图案，这意味着它们的图案能以任何放大率或缩小率生成和复制。描述蕨类植物的数学公式是根据迈克尔·巴恩斯利的名字命名的，它是第一个显示这种混沌状态是不可预知的，而且一般是遵循确定性法则(以非线性循环方程组为基础)。也就是说，利用巴恩斯利的蕨类植物公式反复生成的任意数字，最终生成一个独一无二的蕨类植物形状的物体。

6.云团

云团

这可能是迄今为止拍到的这种形式的最长云团

上图中的海上层状云团是“阿卡”卫星在非洲西海岸附近的南太平洋上空拍到的。分形云团图案，被一系列斜纹状云团分开。据美国宇航局“地球观测台”说，在这种连续云团中看到这么明显的分界线，实属罕见，至今科学家还无法解释清楚它是如何形成的。

据美国宇航局说，下图里长达200英里(321.87公里)的一系列云旋，它可能是迄今为止拍到的这种形式的最长云团。这些云旋又被称作冯·卡门云街(von Kármán cloud streets)，是根据已故流体动力学家西奥多·冯·卡门的名字命名的。当低空云团被岛屿等物体中断时，就会形成云街。机翼下方的风有时也会形成这种图案。

7.叶子

叶子

很多植物的分枝和叶片形状都遵循着简单的递推公式。具有讽刺意味的是，沿主干道、二级和三级路线进行的森林砍伐模式，也形成了类似图案，例如下图中显示的巴西西部朗多尼亚州的森里砍伐图，这是亚马逊流域森林砍伐最严重的一个地区。

8. 峡谷

峡谷

亚利桑那州柴利峡谷国家古迹的伪彩色图

上面这张美国大峡谷的伪彩色图，展示的是由科罗拉多河在长达数百万年间创造的一个分形图案。图片上的红色代表植被区。下图显示的是亚利桑那州柴利峡谷国家古迹的伪彩色图。美国国家公园管理局称，它是北美洲最长的连续性有人居住峡谷地形。

9.闪电

闪电

闪电在向地面移动时，它的路径是逐步形成的，闪电把空气转变成等离子体。

10.孔雀毛

11.雪花

12.瀑布

瀑布

瀑布跟峡谷类似，水流从陡峭的岩脊一侧流过时，不规则的岩石组合和重力导致重复图案产生。

13.河流三角洲

育空河在汇入阿拉斯加州近海的白令海以前，分支成数千条支流。该河从图上的左侧流过，白令海位于图片的左侧较远处。

数学上最有名的分形应该是Mandelbrot（曼德尔布罗特）集合。下面的视频带你进入一个震撼的分形世界。这里你可以感受到不同尺度下的Mandelbrot集合，以及其内涵的尺度不变性和结构的丰富性。尺度不变性和结构的丰富性是分形的最大特征。

视频来源于youtube

参考文献

https://en.m.wikipedia.org/wiki/List_of_fractals_by_Hausdorff_dimension

资料来源：超级数学建模、最强大脑、返朴等网络，版权归原作者所有。

品牌策划13501979518