📝前言说明：
本专栏主要记录本人的基础算法学习以及刷题记录，使用语言为C++。
每道题我会给出LeetCode上的题号（如果有题号），题目，以及最后通过的代码。没有题号的题目大多来自牛客网。对于题目的讲解，主要是个人见解，如有不正确，欢迎指正，一起进步！

🎬个人简介：努力学习ing
📋本专栏：C++刷题专栏
📋其他专栏：C++学习笔记，C语言入门基础，python入门基础，python刷题专栏
🎀CSDN主页 愚润泽

226. 翻转二叉树

题目链接

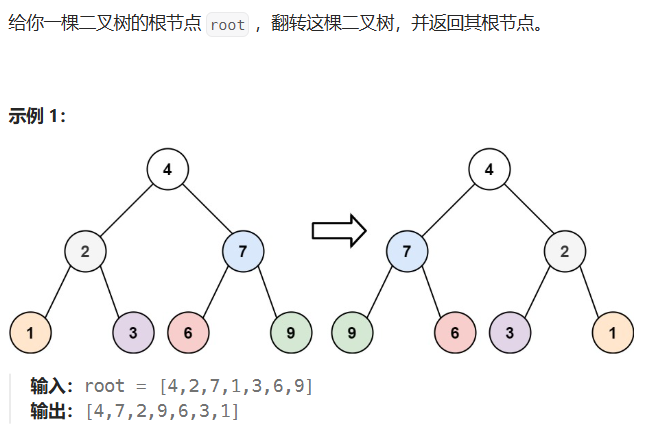
大问题化小问题：根节点的左右子树要反转，左右子树的左右子树也要反转
注意点：将子树反转后的结果记录，供上一层翻转使用

TreeNode* invertTree(TreeNode* root) 
{// 左子树成为右子树if(root == nullptr){return nullptr;}auto left = invertTree(root->left); // 递归左子树，并且将左子树的反转结果记录auto right = invertTree(root->right);root->left = right;root->right = left; // 记录后，用于翻转本层return root;
}

110. 平衡二叉树

题目链接

大问题化小问题：一棵树如果是平衡二叉树，则他的左右子树也是平衡二叉树。
将问题转换为获取高度的问题，判断高度差是否大于1

class Solution {
public:int get_h(TreeNode* root){if(root == nullptr) {return 0;}return max(get_h(root->left), get_h(root->right)) + 1;}bool isBalanced(TreeNode* root) {if(root ==nullptr){return true;}return (abs(get_h(root->left) - get_h(root->right)) <= 1) && isBalanced(root->left) && isBalanced(root->right);}
};

102. 二叉树的层序遍历

题目链接

这道题和之前做过的题不同在：需要将每一层的元素单独存在一个vector里面，要怎么实现呢？
原来我们只用一个队列进行操作，队头元素遍历后就出队列，然后把它的孩子入队列。但是这种操作我们没办法进行层与层的区分。
为了区分层与层，我们可以用两个队列：1,当前遍历的节点队列，2,下一层要遍历的节点队列。不难发现，当前要遍历的所有节点的孩子就是下一层要遍历的节点。所以我们只需要让孩子入队列时入到不同的队列即可。

class Solution {
public:vector<vector<int>> levelOrder(TreeNode* root) {vector<vector<int>> ans;if(root == nullptr) // 针对空树{return {}; // 用{}表示空vector} vector<TreeNode*> cur = {root}; // 非空树时，当层要遍历的节点while(!cur.empty()){vector<int> vals; // 用来存放当前层节点的值vector<TreeNode*> nxt; // 下一层要遍历的节点for(auto node: cur) // queue是容器适配器，没有迭代器{vals.push_back(node->val);if (node->left) nxt.push_back(node->left); // 要确保入队列的不是空指针，不然node->val 会出问题if (node->right) nxt.push_back(node->right);}cur = move(nxt); // 相当于一次全出栈了，并且更换了 curans.push_back(vals);}return ans;}
};

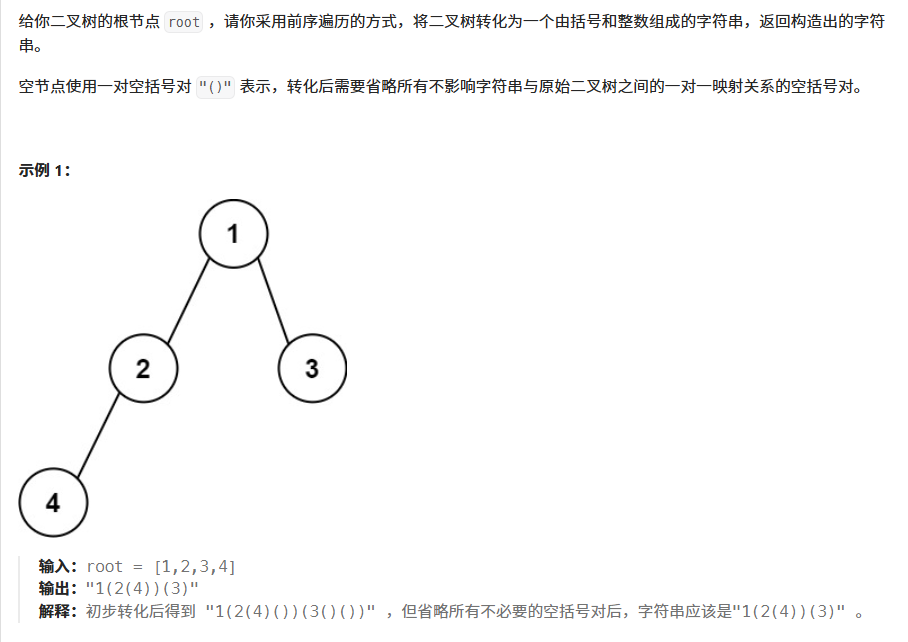
606. 根据二叉树创建字符串

题目链接

class Solution {
public:string ans;void dfs(TreeNode* root){if(!root) return;string ch = to_string(root -> val);ans += ch;if(!root->left && root->right)ans += "()";if(root->left){ans += "(";dfs(root->left);ans += ")";}if(root->right){ans += "(";dfs(root->right);ans += ")";}}string tree2str(TreeNode* root) {dfs(root);return ans;}
};

• 唯一麻烦的就是：处理什么时候加()的问题

102. 二叉树的层序遍历

题目链接

• 利用队列辅助：每次从队头取出一个节点处理，并将其子节点（下一层）放入队尾。
• 如何分层？当还没有开始操作时，当前queue中节点的个数就是当前层节点的个数。

class Solution {
public:vector<vector<int>> levelOrder(TreeNode* root) {if(!root) return {};vector<vector<int>> ans;queue<TreeNode*> q;q.push(root); while(!q.empty()){vector<int> path; // path 的生命周期只有一次while循环for(int i = q.size(); i > 0; i--){auto node = q.front(); // 获得队头节点path.push_back(node -> val);q.pop(); // 输出队头节点if (node->left) q.push(node->left);if (node->right) q.push(node->right);}ans.emplace_back(path);}return ans;}
};

107. 二叉树的层序遍历 II

题目链接

只需将上一题的答案翻转即可。记住队列的用途是确保FIFO，使得左边的比右边的先出，保证的是一层的顺序。

class Solution {
public:vector<vector<int>> levelOrderBottom(TreeNode* root) {if(!root) return {};vector<vector<int>> ans_tmp;queue<TreeNode*> q;q.push(root);while(!q.empty()){vector<int> path;for(int i = q.size(); i > 0; i--){auto node = q.front();path.push_back(node->val);q.pop();if(node -> left) q.push(node->left);if(node -> right) q.push(node->right);}ans_tmp.emplace_back(path);}vector<vector<int>> ans;for(int i = ans_tmp.size() - 1; i >= 0; i--)ans.emplace_back(ans_tmp[i]);return ans;}
};

236. 二叉树的最近公共祖先

题目链接

class Solution {
public:// 以 root 为根节点的数包同时包含 p 和 q 则代表该节点是祖先bool dfs(TreeNode* root, TreeNode* node) // node是要寻找的节点{if(!root) return false;return root == node || dfs(root->left, node) || dfs(root->right, node);}TreeNode* solution(TreeNode* root, TreeNode* p, TreeNode* q){// 后续遍历，深度可以尽可能大if(!root) return nullptr; TreeNode* lret = solution(root->left, p, q);TreeNode* rret = solution(root->right, p, q);// 一旦有结果立马返回if(lret || rret) return lret? lret : rret; // 如果lret有，则一定是lret先返回if(dfs(root, p) && dfs(root, q))return root;elsereturn nullptr;}TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {return solution(root, p, q);}
};

当然，代码写的不是很优雅。

🌈我的分享也就到此结束啦🌈
要是我的分享也能对你的学习起到帮助，那简直是太酷啦！
若有不足，还请大家多多指正，我们一起学习交流！
📢公主，王子：点赞👍→收藏⭐→关注🔍
感谢大家的观看和支持！祝大家都能得偿所愿，天天开心！！！