七年级数学(上)最全的知识点
第1章 有理数
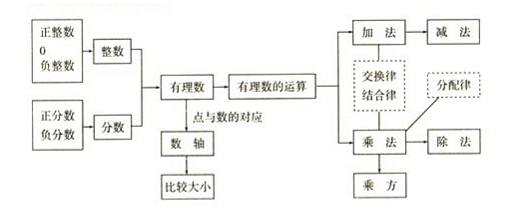
一、 知识框架
二、知识概念
1、 有理数:

2 、数轴:数轴是规定了原点、正方向、单位长度的一条直线(三者缺一不可);
注意:①在数轴上到定点距离等于定长的点有两个。(例如到原点距离等于2的点有两个:±2)
②在数轴上,右边的表示的数大于左边的点表示的数;
③原点左侧的为负数,原点右侧的为正数;
④ 在数轴上的距离:右边的点表示的数-左边的点表示的数;
或者两点表示的数差的绝对值 .
3 、相反数:
(1)只有符号不同的两个数互为相反数;0的相反数还是0;
(2)相反数的和为0 ↔ a+b=0 ↔a、b互为相反数.
4、 绝对值:
(1)正数的绝对值是其本身,0的绝对值是0,负数的绝对值是它的相反数;
注意:在数轴上表示数a的点到原点的距离,叫做a的绝对值.
(2) 绝对值可表示为:
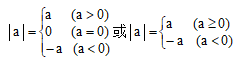
绝对值的问题经常 分类讨论;
5、 有理数比大小:
(1)数轴上不同的两个点表示的数,右边点表示的数总比左边点表示的数大;
(2) 正数大于0,0大于负数,正数大于负数;
(3) 两个负数比较大小,绝对值大的反而小;
(4) 大数-小数> 0,小数-大数< 0;
(5)正数大于一切负数 .
6、 互为倒数:乘积为1的两个数互为倒数;
注意:0没有倒数;若 a≠0,那么a的倒数是;若ab=1Ûa、b互为倒数.
7、 有理数加法法则:
(1)同号两数相加,取与加数相同的符号,并把绝对值相加;
(2)异号两数相加,绝对值相等时和为0; 绝对值不相等时,取绝对值较大的符号,并用较大的绝对值减去较小的绝对值;
(3)一个数与0相加,仍得这个数.
8 、有理数加法的运算律:
(1)加法的交换律: a+b=b+a ;
(2)加法的结合律: (a+b)+c=a+(b+c).
9 、有理数减法法则:减去一个数,等于加上这个数的相反数;即a-b=a+(-b).
10、 有理数乘法法则:
(1)两数相乘, 同号为正,异号为负,并把绝对值相乘;
(2)任何数同零相乘都得零;
(3)几个数相乘,有一个因数为0,积为0;
几个不为0的数相乘,积的符号由负因数的个数决定.当负因数有奇数个时,积为负; 当负因数有偶数个时,积为正。
11、 有理数乘法的运算律:
(1)乘法的交换律: ab=ba;
(2)乘法的结合律: (ab)c=a(bc);
(3)乘法的分配律: a(b+c)=ab+ac.
12 、有理数除法法则:除以一个不为0的数等于乘以这个数的倒数;
注意:0不能做除数.
13 、有理数乘方的法则:
(1)正数的任何次幂都是正数;
(2)负数的奇次幂是负数;负数的偶次幂是正数;
(3)任何非零数的零次幂等于1(a 0 =1,a≠0);
注意:当n为正奇数时:(-a) n =-a n 或(a-b) n =-(b-a) n ,
当n为正偶数时: (-a) n =a n 或(a-b) n =(b-a) n .
14 、乘方的定义:
(1)求若干个相同因数的积的运算,叫做乘方;
(2)乘方运算a n 中,相同的因数a叫做底数,相同因 数的个数n叫做指数,乘方的结果a n 叫做幂;
(3)a n 既可以表示n个a相乘,又表示n个a相乘的结果.
15 、科学记数法:把一个大于10的数记成a×10 n 的形式,其中a是整数数位只有一位的数,这种记数法叫科学记数法 (1≤a小于10).
16、近似数的精确位:一个近似数,四舍五入到某一位,就说这个近似数精确到那一位 .
近视值与它的准确值的差,叫做误差;误差可能是正数也可能是负数。误差的绝对值越小,近似值就越接近准确值 .
17、有效数字:从左边第一个不为零的数字起,到精确的位数止,所有数字,都叫这个近似数的有效数字 .
18、 混合运算法则:先乘方,再乘除,后加减,如果有括号,先进行括号里的运算 .
第2章 整式加减
一.知识框架
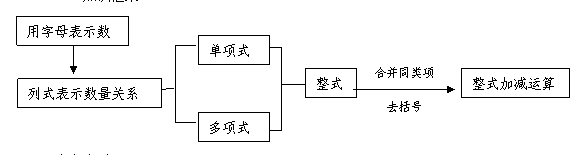
二、 知识概念
1、代数式:例24a,R2 ,a+b……像这样用加、减、乘、除及乘方等运算符号把数或表示数的字母连接而成的式子,叫代数式.
注:① 单个的数或字母也是代数式,例如7,a等;
②代数式中如果出现乘号,可写成 “ · ”或不写,数字与数字相乘时,“x”不能省略;
③如果式子中出现除法,一般写成分数形式;
2、单项式: 在代数式中,3a, R2 , -x都是数与字母的积,像这样的代数式叫做单项式; 单个的数或字母也是单项式,例如7,a等;
3、单项式的系数与次数:单项式中不为零的数字因数,叫单项式的系数;单项式中所有字母的指数之和叫作这个单项式的次数;
4、多项式:几个单项式的和叫多项式;
5、多项式的项数与次数:
① 在多项里,每个单项式(连同符号)叫多项式的项;
② 其中不含字母的项叫常数项;
③ 多项式中所含单项式的个数就是多项式的项数;
④多项式里,次数最高的项的次数叫这个多项式的次数。
6、同类项: 所含的字母相同,并且相同字母的指数也分别相同的项叫做同类项;
注:① 所含的字母相同;
② 相同字母的指数也分别相同;
③同类项与系数无关,与字母的排列顺序也无关.
7、合并同类项:把多项式中的同类项合并成一项叫做合并同类项;
同类项的系数相加,所得的结果作为系数,字母和字母的指数不变.
注:①去括号时注意符号的变化(因式的符号和括号前面的符号同号得正,异号得负);
②合并同类项不要漏项 .
第3章 一次方程与方程组
一. 知识框架
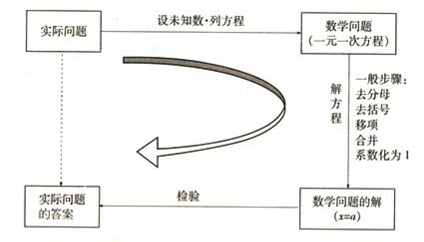
二.知识概念
1.一元一次方程:只含有一个未知数,未知数的次数是1,且等式两边都是整式的方程是一元一次方程.
2.等式的基本性质:

3.一元一次方程解法的一般步骤:去分母……去括号……移项(移项要变符号)……合并同类项……系数化为1 ……(检验方程的解).
4.列一元一次方程解应用题:重点是找等量关系 .
①找出表示相等关系的关键字,例如:“和、倍、大、小、多、少等等”;
②利用这些关键字列出文字等式;
③并且据题意设出未知数,列出方程;
④解方程(验根) .
注: 行程问题一般用画图解决, 认真审题,依照题意画出有关图形,使图形各部分具有特定的含义,通过图形找相等关系是解决问题的关键 .
5.列方程解应用题的常用公式:
(1)行程问题: 距离=速度x时间;
(2)工程问题: 工作量=工效 x工时;
(3)比率问题: 部分=全体 x比率;
(4)顺逆流问题: 顺流速度=静水速度+水流速度,逆流速度=静水速度-水流速度;
(5)商品价格问题: 售价=定价 x折扣 ,利润=售价-成本;
(6)周长、面积、体积问题: C圆=2πR,S圆=π R2 ,C长方形=2(a+b),
S长方形=ab, C正方形=4a,
S正方形=a 2 ,S环形=π( R2 - r2 ),V长方体=abc ,
V正方体=a 3 ,V圆柱=π R2 h,V圆锥=π R2 h.
6、解二元一次方程组常用的方法:
(1)代入消元法:从一个方程中求出某一个未知数的表达式,再把它“代入”到另一个方程,进行求解,这种方法叫做代入消元法,简称代入法;
(2)加减消元法;把两个方程的两边分别相加或相减消去一个未知数的方法,叫做加减消元法,简称加减法;
第4章 直线与角
一、知识框架
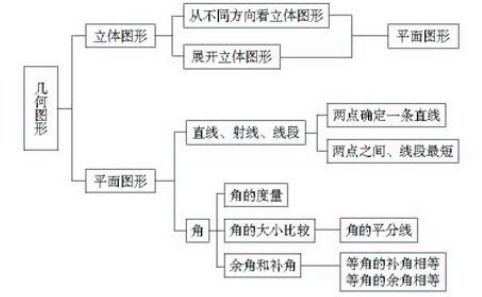
1、直线没有端点,射线有一个端点,线段有两个端点;
2、经过两点有且只有一条直线;
3、两直线相交只有一个交点;
4、两点之间的所有连线中,线段最短;
5、角的平分线是射线;
6、同角(或等角)的补角相等;
7、同角(或等角)的余角相等;
第5章 数据的收集(略)
关注公众号跟着秀才学习,觉得点击好右下角分享给小伙伴们。
免责声明:秀才整理,部分图片来源于网络,侵删。 参考:沪科版数学教材。