八下数学 | 平行四边形
【动点问题】4大常考题型
题型一【矩形中的动点问题】
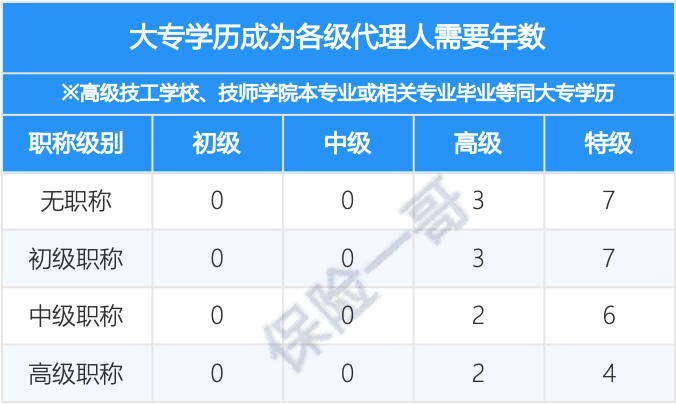
已知,在矩形ABCD中,AB=4 cm,BC=8 cm,AC的垂直平分线EF分别交AD,BC于点E,F,垂足为O.

(1)如图①,连接AF,CE,试说明四边形AFCE为菱形,并求AF的长;
解:∵四边形ABCD是矩形,∴AD∥BC.
∴∠CAD=∠ACB,∠AEF=∠CFE.
∵EF垂直平分AC,垂足为O,
∴OA=OC.
∴△AOE≌△COF.∴OE=OF.
∴四边形AFCE为平行四边形.
又∵EF⊥AC,∴四边形AFCE为菱形.
设AF=CF=x cm,则BF=(8-x)cm,
在Rt△ABF中,AB=4 cm,
由勾股定理得42+(8-x)2=x2,解得x=5.
∴AF=5 cm.
(2)如图②,动点P,Q分别从A,C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中,已知点P的速度为5 cm/s,点Q的速度为4 cm/s,运动时间为t s,当以A,C,P,Q四点为顶点的四边形是平行四边形时,求t的值.
解:显然当P点在AF上,Q点在CD上时,A,C,P,Q四点不可能构成平行四边形;
同理P点在AB上,Q点在DE或CE上时,也不可能构成平行四边形.因此只有当P点在BF上,Q点在ED上时,才能构成平行四边形,
如图,连接AP,CQ,则以A,C,P,Q四点为顶点的四边形是平行四边形,此时PC=QA.
∵点P的速度为5 cm/s,点Q的速度为4 cm/s,运动时间为t s,
∴PC=5t cm,QA=(12-4t)cm.
∴5t=12-4t,解得t=4/3.
∴以A,C,P,Q四点为顶点的四边形是平行四边形时,t=4/3.
题型二【菱形中的动点问题】
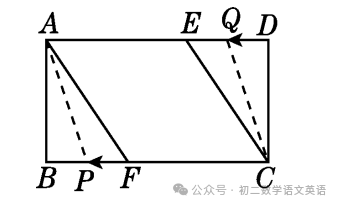
如图,在菱形ABCD中,∠B=60°,动点E在边BC上,动点F在边CD上.
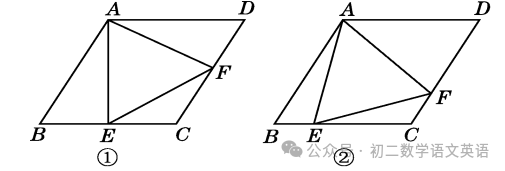
(1)如图①,若E是BC的中点,∠AEF=60°,求证:BE=DF;
解:证明:如图①,连接AC.
∵在菱形ABCD中,∠B=60°,
∴AB=BC=CD,∠BCD=180°-∠B=120°.
∴△ABC是等边三角形.
又∵E是BC的中点,
∴AE⊥BC.∵∠AEF=60°,
∴∠FEC=90°-∠AEF=30°.
∴∠CFE=180°-∠FEC-∠BCD
=180°-30°-120°=30°.
∴∠FEC=∠CFE.∴EC=CF.∴BE=DF.
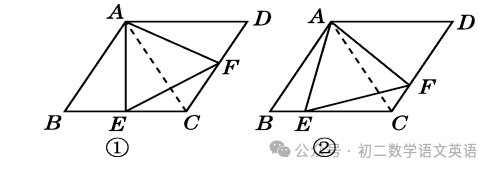
(2)如图②,若∠EAF=60°,求证:△AEF是等边三角形.
解:如图②,连接AC.由(1)知△ABC是等边三角形,
∴AB=AC,∠ACB=∠BAC=60°.
又∵∠EAF=60°,∴∠BAE=∠CAF.
∵∠BCD=120°,∠ACB=60°,
∴∠ACF=60°=∠B.
∴△ABE≌△ACF.∴AE=AF.
∴△AEF是等边三角形.
题型三【正方形中的动点问题
如图,正方形ABCD的边长为8 cm,E,F,G,H分别是AB,BC,CD,DA上的动点,且AE=BF=CG=DH.
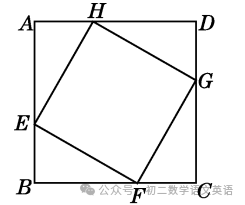
(1)求证:四边形EFGH是正方形;
解:证明:如图,∵四边形ABCD为正方形,
∴∠A=∠ABC=∠C=∠ADC=90°,
AB=BC=CD=AD.
∵AE=BF=CG=DH,
∴AH=BE=CF=DG.
∴△AEH≌△BFE≌△CGF≌△DHG.
∴∠1=∠2,EH=EF=FG=GH.
∴四边形EFGH为菱形.
∵∠1+∠3=90°,∠1=∠2,
∴∠2+∠3=90°.
∴∠HEF=90°.
∴四边形EFGH为正方形.
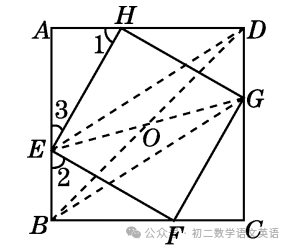
(2)判断直线EG是否经过一个定点,并说明理由.
解:直线EG经过一个定点.理由如下:如图,连接BD,DE,BG,EG.设EG与BD交于O点.
∵BE綊DG,
∴四边形BGDE为平行四边形.
∴BD,EG互相平分.∴BO=OD.
∴点O为正方形的中心.
∴直线EG必过正方形的中心.
题型四【平行四边形中的动点问题】
如图,在▱ABCD中,E,F两点在对角线BD上运动(E,F两点不重合),且保持BE=DF,连接AE,CF.请你猜想AE与CF有怎样的数量关系和位置关系,并对你的猜想加以证明.
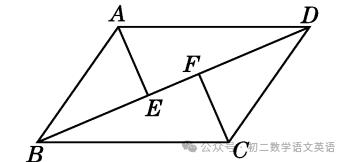
解:AE=CF,AE∥CF.证明如下:
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD.
∴∠ABE=∠CDF.在△ABE和△CDF中,
∵AB=CD,∠ABE=∠CDF,BE=DF,
∴△ABE≌△CDF.
∴AE=CF,∠AEB=∠CFD.
∵∠AEB+∠AED=∠CFD+∠CFB=180°,
∴∠AED=∠CFB.
∴AE∥CF.
若您觉得有用,点个【在看】或分享【朋友圈】吧!
公众号回复“0”免费观看所有知识点视频
整式——宇宙的语言从算式到方程——由已知到未知解一元一次方程——希尔伯特23问
↓↓↓点击“阅读原文”, 观看数学所有知识点视频