力扣题解106：从中序与后序遍历序列构造二叉树-海口c网

力扣题解106：从中序与后序遍历序列构造二叉树

article/2025/8/11 15:56:33

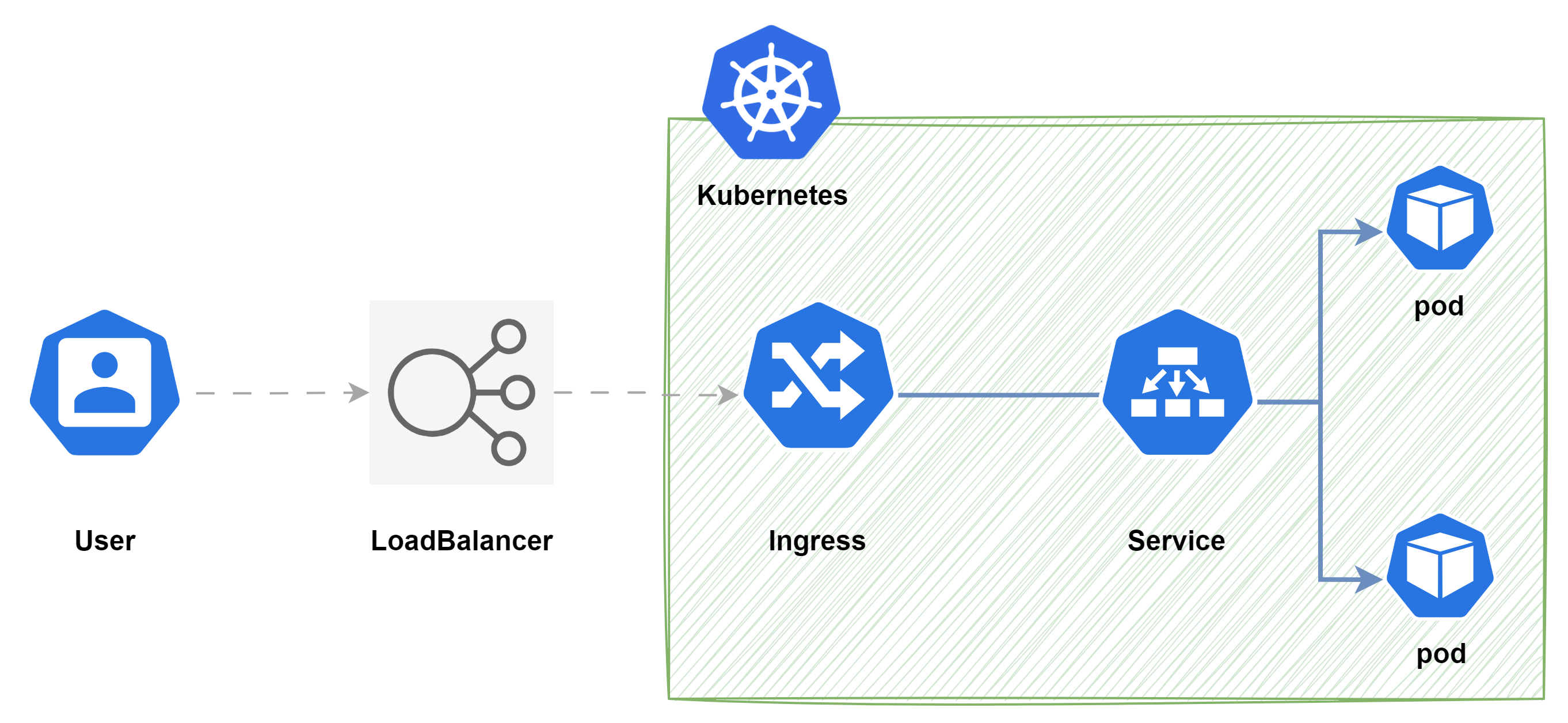
一、题目内容

题目要求根据二叉树的中序遍历序列和后序遍历序列来重建二叉树。具体来说，我们需要利用中序遍历序列和后序遍历序列的特点，通过递归的方法逐步构建出完整的二叉树。

中序遍历序列的特点是：左子树 -> 根节点 -> 右子树。后序遍历序列的特点是：左子树 -> 右子树 -> 根节点。因此，后序遍历的最后一个元素一定是根节点。通过这个根节点，我们可以在中序遍历序列中找到左子树和右子树的分界点，从而递归地构建左右子树。

我们需要声明一些变量来记录当前的遍历范围和递归的状态。在递归过程中，我们需要不断更新这些变量的值，以确保正确地构建每个子树。

二、题目分析

输入和输出

输入：

两个整数数组 inorder 和 postorder。
- inorder：二叉树的中序遍历序列。
- postorder：二叉树的后序遍历序列。

输出：

构建好的二叉树的根节点（TreeNode 类型）。

递归函数 `traversal` 的逻辑

参数：

inorder：当前子树的中序遍历序列。
postorder：当前子树的后序遍历序列。

逻辑：

如果 postorder 为空，说明当前子树为空，返回 NULL。
获取当前子树的根节点值 rootvalue，即 postorder 的最后一个元素。
创建根节点 root，值为 rootvalue。
如果 postorder 只有一个元素，说明当前子树只有一个节点，直接返回 root。
在中序遍历中找到根节点的位置 mid。
根据 mid，将中序遍历序列划分为左子树和右子树。
根据左子树的大小，将后序遍历序列划分为左子树和右子树。
递归构建左子树和右子树。
返回根节点 root。

三、代码解答

1. C++代码

class Solution {
public:// 主函数，用于调用递归函数并返回结果TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {if (postorder.empty() || inorder.empty()) return NULL;return traversal(inorder, postorder);}private:// 辅助递归函数TreeNode* traversal(vector<int>& inorder, vector<int>& postorder) {// 如果 postorder 为空，说明当前子树为空if (postorder.empty()) return NULL;// 获取当前子树的根节点值int rootvalue = postorder.back();TreeNode* root = new TreeNode(rootvalue);// 如果 postorder 只有一个元素，说明当前子树只有一个节点if (postorder.size() == 1) return root;// 在中序遍历中找到根节点的位置auto it = find(inorder.begin(), inorder.end(), rootvalue);int mid = distance(inorder.begin(), it);// 根据 mid，将中序遍历序列划分为左子树和右子树vector<int> leftInorder(inorder.begin(), inorder.begin() + mid);vector<int> rightInorder(inorder.begin() + mid + 1, inorder.end());// 根据左子树的大小，将后序遍历序列划分为左子树和右子树postorder.pop_back(); // 移除当前根节点vector<int> leftpostorder(postorder.begin(), postorder.begin() + leftInorder.size());vector<int> rightpostorder(postorder.begin() + leftInorder.size(), postorder.end());// 递归构建左子树和右子树root->left = traversal(leftInorder, leftpostorder);root->right = traversal(rightInorder, rightpostorder);return root;}
};

详细注释

成员变量

TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder)：主函数，用于调用递归函数并返回结果。
TreeNode* traversal(vector<int>& inorder, vector<int>& postorder)：辅助递归函数，用于构建当前子树。

辅助递归函数 `traversal`

TreeNode* traversal(vector<int>& inorder, vector<int>& postorder) {// 如果 postorder 为空，说明当前子树为空if (postorder.empty()) return NULL;// 获取当前子树的根节点值int rootvalue = postorder.back();TreeNode* root = new TreeNode(rootvalue);// 如果 postorder 只有一个元素，说明当前子树只有一个节点if (postorder.size() == 1) return root;// 在中序遍历中找到根节点的位置auto it = find(inorder.begin(), inorder.end(), rootvalue);int mid = distance(inorder.begin(), it);// 根据 mid，将中序遍历序列划分为左子树和右子树vector<int> leftInorder(inorder.begin(), inorder.begin() + mid);vector<int> rightInorder(inorder.begin() + mid + 1, inorder.end());// 根据左子树的大小，将后序遍历序列划分为左子树和右子树postorder.pop_back(); // 移除当前根节点vector<int> leftpostorder(postorder.begin(), postorder.begin() + leftInorder.size());vector<int> rightpostorder(postorder.begin() + leftInorder.size(), postorder.end());// 递归构建左子树和右子树root->left = traversal(leftInorder, leftpostorder);root->right = traversal(rightInorder, rightpostorder);return root;
}

空子树检查：如果 postorder 为空，说明当前子树为空，返回 NULL。
获取根节点值：从后序遍历中获取当前子树的根节点值 rootvalue，即 postorder.back()。
创建根节点：创建根节点 root，值为 rootvalue。
单节点子树检查：如果 postorder 只有一个元素，说明当前子树只有一个节点，直接返回 root。
找到根节点在中序遍历中的位置：在中序遍历中找到根节点的位置 mid。
划分中序遍历序列：根据 mid，将中序遍历序列划分为左子树和右子树。
划分后序遍历序列：根据左子树的大小，将后序遍历序列划分为左子树和右子树。
递归构建左子树和右子树：递归调用 traversal 函数构建左子树和右子树。
返回根节点：返回构建好的根节点 root。

主函数 `buildTree`

TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {if (postorder.empty() || inorder.empty()) return NULL;return traversal(inorder, postorder);
}