D. Andrey and Escape from Capygrad

题目：

 

思路：

很有思维的一题，非常nice

题目给了我们一个很有意思的条件，如果 x 在 l[i] ~ r[i] 之间，那么就可以跳跃到 a[i] ~ b[i] 之间，那么一个很显然的想法，我们可以记录每个区间内的数最远能跳到哪里去，查询时枚举即可

但是这样的做法显然会超时，每次查询都是 n 的复杂度，所以我们得优化一下，那我们来好好利用题意

首先思路没错，那么该如何优化呢？其实我们可以发现一个事情，那就是我们其实可以做一个类似区间合并的操作，因为如果两个a~b区间可以到达，那么这两个区间就是同一个区间

接下来我们考虑如何合并，由于题目给的条件是处于 l`~ r 就能跳跃，那么我们可以选择 l ~ b 这个区间作为合并的区间，为什么呢？因为如果处于 b 之前的点肯定是跳到 b 或者合并的区间更好，而 b 点之后的点不跳跃至 a~b 区间之内可能会更好，所以我们这里合并每个 l ~ b 区间，那么如何合并区间呢？

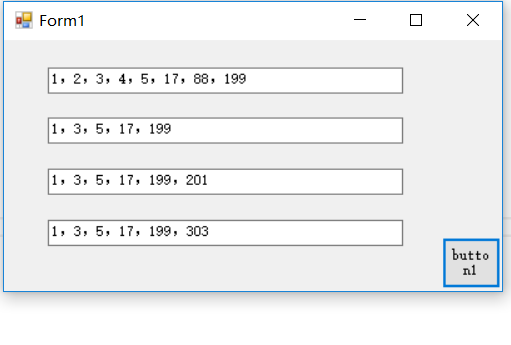
我们可以使用差分，如果 sum 等于 0，说明合成了一个大区间，否则就继续合并，然后对于合并好的区间我们用一个数组存储起来，那么最后肯定是一个类似下图的模样

即最后的所有区间都不会有交集，对于每个区间我们都记录其 l 和 r

然后就是查询操作了，对于查询操作，我们只需要考虑它在哪个大区间内即可，显然暴力枚举不行，所以我们得考虑优化，可以发现最后的区间的左端点都是单调递增的，所以我们考虑二分

我们找到第一个左端点大于 x 的区间，那么这个区间的前一个的左端点肯定就在 x 左边，然后选择跳or不跳两个操作，即 x = max(x,r)，因为我们的 x 值可能大于 r 但小于下一个 l，所以我们得取最大值

小技巧：对于 pair<int,int> 也是可以使用二分的，只不过查询的值也得是 PII 类型，查询规则就是先比第一个，再比第二个

代码：

#include <iostream>
#include <algorithm>
#include<cstring>
#include<cctype>
#include<string>
#include <set>
#include <vector>
#include <cmath>
#include <queue>
#include <unordered_set>
#include <map>
#include <unordered_map>
#include <stack>
#include <memory>
using namespace std;
#define int long long
#define yes cout << "Yes\n"
#define no cout << "No\n"
void solve()
{int n;std::cin >> n;vector<pair<int, int>> chafeng;vector<pair<int, int>> allrg;allrg.push_back({ -1,-1 });for (int i = 0; i < n; i++){int l, r;std::cin >> l >> r >> r >> r;chafeng.push_back({ l,1 });chafeng.push_back({ r + 1,-1 });}sort(chafeng.begin(), chafeng.end());int last = 0;while(last != chafeng.size()){int sum = 0;int l = chafeng[last].first;int sta = 0;while (sum != 0 || !sta){sum += chafeng[last].second;last++;sta = 1;}allrg.push_back({l,chafeng[last-1].first-1});}int q;std::cin >> q;for (int i = 0; i < q; i++){int x;std::cin >> x;//确保只和 x 相关pair<int, int> ask = { x, 1e9 + 1 };auto iter = upper_bound(allrg.begin(), allrg.end(), ask);iter--;int ans = max(x, iter->second);cout << ans << ' ';}cout << endl;
}signed main()
{std::cin.tie(0)->sync_with_stdio(false);int t = 1;std::cin >> t;while (t--){solve();}return 0;
}