离心率是圆锥曲线中的一个重要的几何性质。
椭圆的离心率:0<e<1;
双曲线的离心率:e>1;
抛物线离心率:e=1。
下面介绍求圆锥曲线离心率的常用方法。
一、直接求出a 、c ,求解e
在求解离心率e,
椭圆中存在:a 2 =b 2 +c 2
双曲线中存在:c 2 =a 2 +b 2
这两个关系对于求解椭圆与双曲线的离心率是非常重要的。
已知标准方程或a 、c 易求时,可利用离心率公式来求解。
例1、 过双曲线M :的左顶点A 作斜率为1 的直线,若与双曲线M 的两条渐近线分别相交于点B 、C ,且|AB|=|BC| ,则双曲线M 的离心率是()
A.
B.
C.
D.
分析:这里的,故关键是求出,即可利用定义求解。
解:易知A (-1 ,0 ),则直线的方程为。直线与两条渐近线和的交点分别为B 、C ,又|AB|=|BC| ,可解得,则故有,从而选A 。
例2、已知椭圆C的短轴长为6,左焦点F到右端点的距离等于9,则椭圆E的离心率等于多少?
解:

二、变用公式,整体求出e
椭圆与双曲线求离心率还有如下变形
例3、已知双曲线的一条渐近线方程为,则双曲线的离心率为()
A.
B.
C.
D.
分析:本题已知,不能直接求出a 、c ,可用整体代入套用公式。
解:由(其中k 为渐近线的斜率)。这里,则,从而选A 。
三、统一定义法
由圆锥曲线的统一定义(或称第二定义)知离心率e 是动点到焦点的距离与相应准线的距离比,特别适用于条件含有焦半径的圆锥曲线问题。
例4、在给定椭圆中,过焦点且垂直于长轴的弦长为,焦点到相应准线的距离为1 ,则该椭圆的离心率为()
A.
B.
C.
D.
解:由过焦点且垂直于长轴的弦又称为通径,设焦点为F ,则轴,知|MF| 是通径的一半,则有。由圆锥曲线统一定义,得离心率,从而选B 。
四、( 等量关系 )利用题目中所给的几何关系或者条件得出a,b,c的关系,然后根据b2 =a 2 -c 2 (椭圆)或者b 2 =c 2 -a 2 (双曲线),消除b,得到关于a,c的方程,从而得到e的方程,继而解出e。
例5、设双曲线的渐近线与抛物线y=x 2 +1相切,则该双曲线的离心率等于多少?
解:

例6、设双曲线(0<a<b)的半焦距为c,直线L过(a,0),(0,b)两点,已知原点到直线的距离为 ,则双曲线的离心率为多少?
解:

五、构造a 、c 的齐次式,解出e
根据题设条件,借助a 、b 、c 之间的关系,构造出a 、c 的齐次式,进而得到关于e 的方程,通过解方程得出离心率e 的值。
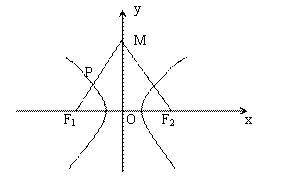
例7、已知、是双曲线的两焦点,以线段F 1 F 2 为边作正,若边的中点在双曲线上,则双曲线的离心率是()
A.
B.
C.
D.
解:如图,设的中点为P ,则点P 的横坐标为,由,由焦半径公式,即,得,有,解得(舍去),故选D 。
六、特殊结论
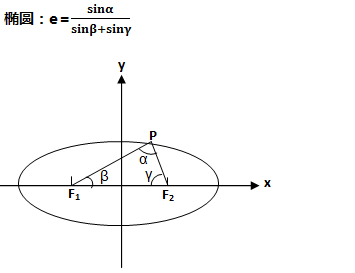
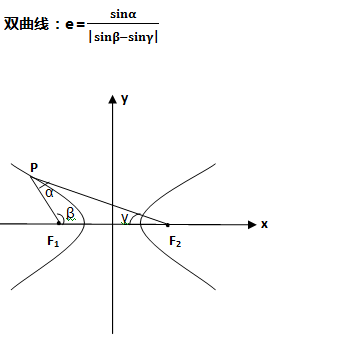
例8、已知F 1 、F 2 是椭圆的两个焦点,过F 1 且与椭圆长轴垂直的直线交椭圆于A、B两点,若△ABF 2 是正三角形,则这个椭圆的离心率是多少?
解:
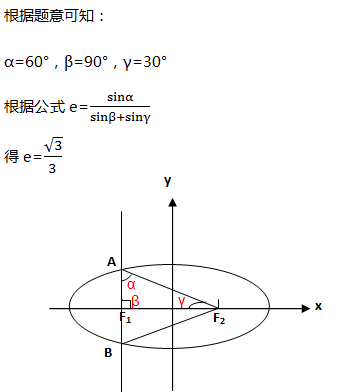
例9、设F 1 ,F 2 分别是双曲线 (a>0,b>0)的左、右焦点,点A在双曲线上,且AF 2 与x轴垂直,若 ,则双曲线的离心率是多少?
解:
若您觉得有用,点个【在看】或分享【朋友圈】吧!
公众号回复“ 0”免费观看所有知识点视频
正数和负数———但丁密码、天堂和地狱
相反数———双生世界 有理数的定义———死亡迷宫的出口