量子力学引人入胜,揭示了微观世界中颗粒的神奇行为。而在这个令人着迷的领域中,复变函数扮演着至关重要的角色。通过复变函数,我们能够深入理解波函数的性质、解析函数的特性,以及路径积分的计算方法。本文将带您一起探索量子力学与复变函数的交汇点,揭开其中的数学奥秘。
一、复变函数的基础知识
1.1 复变函数简介
复变函数是一种包含复数作为自变量和因变量的函数。复数由实部和虚部组成,可以用复平面上的点来表示。复变函数与实变函数之间存在一些重要的区别。例如,实变函数可以通过导数来描述其变化率,而复变函数则需要借助复数的解析性质,如柯西-黎曼条件和解析函数的级数展开。
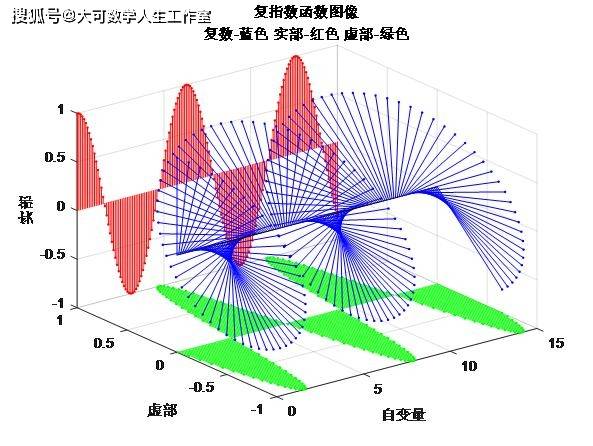
1.2 复数运算规则
在复变函数中,我们需要熟悉复数的基本运算规则。例如,复数的加法与减法可以分别按照实部和虚部进行计算,而复数的乘法和除法则涉及到复数的模和幅角的相乘和相除。这些运算规则为后续讨论量子力学中的复变函数提供了基础。

1.3 复平面表示
复平面是描述复数的有力工具。复数可以由复平面上的点表示,实部和虚部分别对应于点在水平和竖直方向上的坐标。复平面的图形化表示使我们能够更直观地理解复变函数及其性质。例如,将复数相乘转化为复平面上的向量相乘,则模表示向量长度的缩放,幅角表示向量旋转的角度。
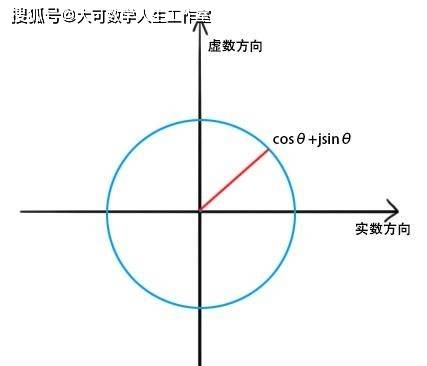
二、复变函数与量子波函数
2.1 薛定谔方程
薛定谔方程是描述量子力学中波函数演化的基本方程。通过复变函数的技术,我们可以更好地理解薛定谔方程及其解析解。以一维自由粒子为例∂²Ψ/∂x² + (2π²mE/ℏ²)Ψ = 0,薛定谔方程可以化简为简单的波动方程形式,例如iℏ∂Ψ/∂t = -(ℏ²/2m)∇²Ψ + VΨ,其中波函数可以表示为复变函数的幅角部分。这种复变函数的表示方式有助于我们理解波函数的传播和干涉现象。

《数学物理方法》是一本由顾樵编写的理论体系科学、严谨、完整且实用的书籍。它将中国教材和国外先进教材相结合,同时也结合了教学实践和其他相关课程的需要,具有很强的实用性。该书内容涉及傅里叶级数、傅里叶变换、拉普拉斯变换、数学物理方程的建立等多个方面,既适合教学使用,也可满足科研需求。此外,书中还包含大量综合性例题,帮助读者更好地掌握问题分析和解决的思路与方法。
2.2 简谐振子问题
简谐振子是量子力学中一个重要的模型,涉及到复变函数的应用。通过解析方法,我们可以求解简谐振子的波函数和能级结构,并运用复变函数的技巧计算量子体系中的平均能量。例如,(-ℏ²/2m)∂²Ψ/∂x² + (1/2)mω²x²Ψ = EΨ。在经典的谐振子问题中,波函数与解析复变函数的幅角部分有相似之处,从而可借助二次型展开来求得波函数的具体表达式。
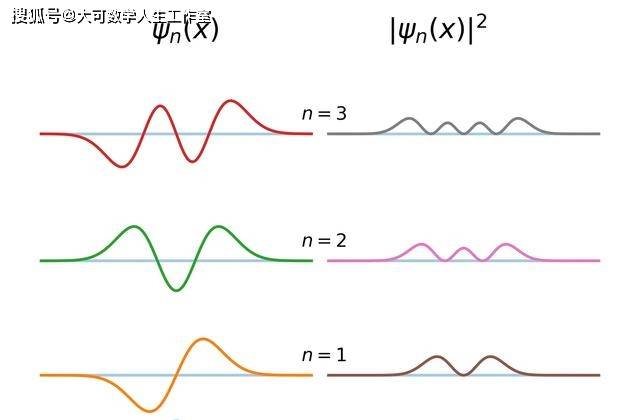
2.3 平均值和不确定性原理
复变函数提供了计算量子力学中平均值和不确定性的数学工具。利用解析函数的性质,我们可以计算波函数的期望值,例如位置期望值和动量期望值⟨x⟩ = ∫x|Ψ|²dx。同时,不确定性原理揭示了测量两个物理量之间不可避免的不确定性Δx Δp ≥ ℏ/2。通过复变函数的技术,我们能够更好地理解量子力学实验结果的含义和概率性质。
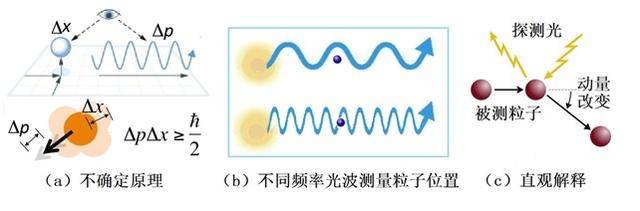
三、复变函数的解析性质与量子体系
3.1 解析函数的概念
解析函数是复变函数中非常重要的概念,具备许多独特的性质。在量子体系中,解析函数的柯西-黎曼条件可以解释为波函数在空间中的光滑性和连续性。通过解析函数的性质,我们可以更好地理解量子体系中的波函数和能级结构。
3.2 奇点结构与量子能级
解析函数的奇点结构对量子能级有重要影响。例如,在无限深方势阱问题中,波函数具有无穷多的奇点,这些奇点对应于波函数在势阱边界处的不连续性。通过研究奇点结构,我们能够理解量子粒子在势能场中的行为规律。
3.3 跃迁规则与解析性质
解析函数的性质还可以揭示量子体系中的跃迁规则P = |C₁|^²,其中 C₁ 表示跃迁的系数。例如,假设一个量子体系中包含两个能级,利用解析函数的方法,我们可以推导出跃迁概率和选择定则。解析性质提供了一种理解粒子跃迁行为的数学解释。
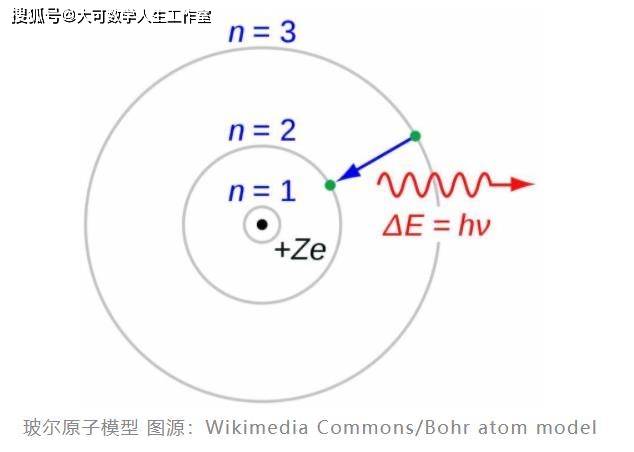
四、复变函数与路径积分理论
4.1 路径积分理论概述
路径积分理论是量子力学中的重要数学框架,复变函数在其中发挥着关键作用。通过复变函数的技术,我们可以推导路径积分理论中的传播子和相互作用的计算公式:Ψ(x_f, t_f; x_i, t_i) = ∫ exp{(i/ℏ)S[x(t)]} Dx(t)。路径积分理论提供了一种全新的视角来描述粒子的传播方式和相互作用。
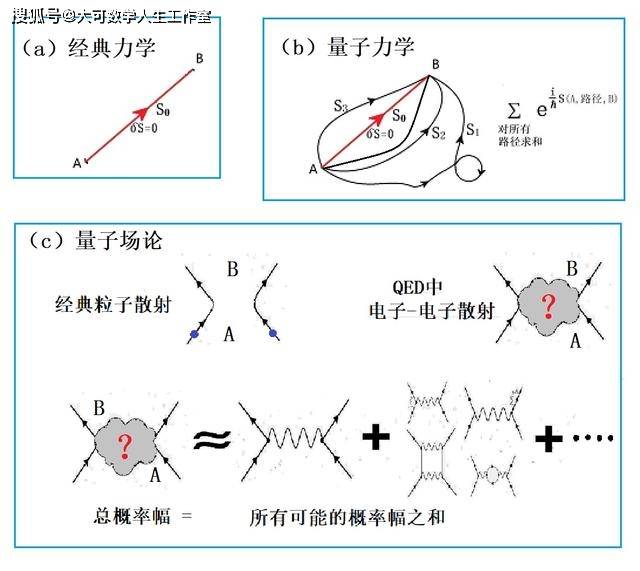
4.2 复变函数的应用
复变函数在路径积分理论中具有广泛的应用。例如,在费曼路径积分中,复变函数可以用于处理路径的相位因子和积分路径选择。通过对复变函数的技巧性应用,我们能够更准确地计算量子体系的性质,如传播子和格林函数等。
《从零开始读懂量子力学》——揭开科学的神秘面纱!量子力学,现代物理学的基石,引领科技的飞速进步。如今,量子依然是新闻热点!我们的书籍旨在为科技爱好者提供系统、严谨的量子力学基础与应用介绍。只需具备高中物理和数学知识,愿意拥抱科学思维,读者定能轻松掌握量子力学原理,了解其在科学体系中的重要性及对现代技术的贡献。
本书以混合讲解方式呈现,既阐述科学理论,又介绍重要实验现象和科学原理的应用。第一篇详解状态叠加、波粒二象性、不确定原理等基本概念;第二篇重点介绍量子力学在凝聚态物理、基本粒子物理以及现代电子技术等领域的应用。
结语
量子力学是一个充满神秘和奇妙的领域,而复变函数在其中扮演着非常重要的角色。通过本文,我们深入了解了复变函数与量子力学的紧密联系,以及复变函数在解析波函数、理解量子体系和应用路径积分理论中的价值。希望这篇文章能够为读者揭开数学与物理之间的奇妙关系,激发大家对量子力学的兴趣和探索欲望。