布隆过滤器-海口c网

布隆过滤器

article/2025/7/12 18:57:37

文章目录

布隆过滤器（Bloom Filter）详解：原理、实现与应用场景
- 一、引言
- 二、布隆过滤器的基本原理
- - 1. 数据结构
  - 2. 插入操作
  - 3. 查询操作
  - 4. 误判率
- 三、布隆过滤器的实现
- 四、布隆过滤器的应用场景
- - 1. 网络爬虫
  - 2. 缓存穿透防护
  - 3. 垃圾邮件过滤
  - 4. 分布式系统
  - 5. 搜索引擎
- 五、布隆过滤器的优缺点
- - 优点
  - 缺点
- 六、布隆过滤器的变种
- - 1. 计数布隆过滤器（Counting Bloom Filter）
  - 2. 动态布隆过滤器（Dynamic Bloom Filter）
  - 3. 加密布隆过滤器（Cryptographic Bloom Filter）
- 七、总结

布隆过滤器（Bloom Filter）详解：原理、实现与应用场景

一、引言

在海量数据处理场景中，我们经常需要快速判断一个元素是否存在于某个集合中。传统的解决方案（如哈希表、树结构）需要存储元素本身，这在数据量极大时会占用大量内存。布隆过滤器（Bloom Filter）则提供了一种空间效率极高的概率型数据结构，它可以告诉你“可能存在”或“一定不存在”，用极小的错误率换取了内存占用的大幅降低。

本文将深入探讨布隆过滤器的原理、实现细节及其在现实场景中的应用，并通过C++代码演示其核心功能。

二、布隆过滤器的基本原理

1. 数据结构

布隆过滤器本质上是一个二进制位数组（通常用位图表示）和一系列哈希函数。初始状态下，整个位数组的所有位都被置为0。

在这里插入图片描述

（布隆过滤器示意图：位数组和多个哈希函数）

2. 插入操作

当要插入一个元素时，布隆过滤器会做以下操作：

用每个哈希函数对元素进行计算，得到多个哈希值
将这些哈希值对位数组长度取模，得到对应的位索引
将这些索引位置的位全部置为1

3. 查询操作

当查询一个元素是否存在时：

用同样的哈希函数对元素进行计算，得到多个哈希值
检查这些哈希值对应的位是否全部为1：
- 如果全部为1，则元素可能存在（存在误判可能）
- 如果有任何一位为0，则元素一定不存在

4. 误判率

布隆过滤器的一个重要特性是存在误判率（False Positive Rate）。即当查询返回“可能存在”时，实际上元素可能并不存在。误判率取决于三个因素：

位数组的大小（m）
哈希函数的数量（k）
已插入元素的数量（n）

误判率公式：
[
P \approx \left(1 - e^{{-\frac{kn}{m}}\right)}k
]

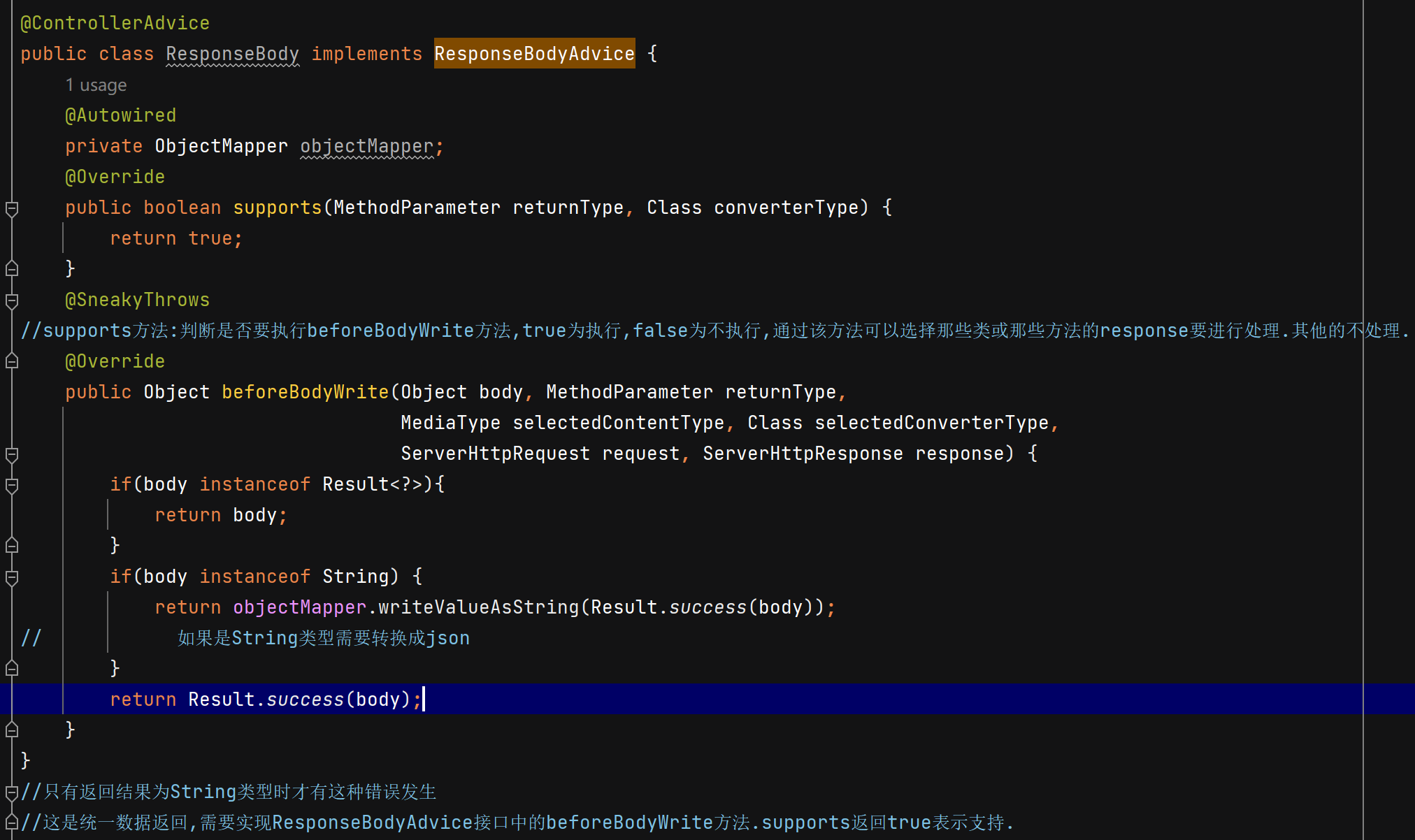
三、布隆过滤器的实现

下面是一个基于C++的布隆过滤器实现示例：

#include <vector>
#include <string>
#include <functional>
#include <bitset>
#include <cmath>template <size_t N>
class BloomFilter {
private:std::bitset<N> bitset_;std::vector<std::function<size_t(const std::string&)>> hash_functions_;public:// 构造函数，接收哈希函数数量explicit BloomFilter(size_t num_hash_functions) {// 使用不同种子的哈希函数for (size_t i = 0; i < num_hash_functions; ++i) {hash_functions_.push_back([i](const std::string& key) {return std::hash<std::string>{}(key + std::to_string(i));});}}// 添加元素到布隆过滤器void add(const std::string& key) {for (const auto& hash_fn : hash_functions_) {size_t index = hash_fn(key) % N;bitset_.set(index);}}// 检查元素是否可能存在bool might_contain(const std::string& key) const {for (const auto& hash_fn : hash_functions_) {size_t index = hash_fn(key) % N;if (!bitset_.test(index)) {return false;}}return true;}// 计算当前误判率double false_positive_rate() const {double m = N;double k = hash_functions_.size();double n = bitset_.count();  // 已设置的位数return std::pow(1.0 - std::exp(-k * n / m), k);}// 重置布隆过滤器void clear() {bitset_.reset();}
};// 优化版本：自动计算最佳哈希函数数量
template <size_t N, size_t ExpectedElements>
class OptimizedBloomFilter : public BloomFilter<N> {
public:OptimizedBloomFilter() : BloomFilter<N>(optimal_num_hash_functions()) {}private:// 计算最优哈希函数数量：k = (m/n) * ln(2)static size_t optimal_num_hash_functions() {return static_cast<size_t>((N / ExpectedElements) * std::log(2));}
};