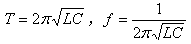伯努利方程实验
描述液体机械运动中的连续性方程、能量方程和动量方程,分别是物理学中的质量守恒定律、能量守恒定律及动量守恒定律在运动液体中的表现形式。伯努利方程以位置水头、压力水头和流速水头,定量表述了液体在运动中的位置势能、压能和动能之间的能量转化关系和联系。通过实验,可以较好的呈现液体在运动中的各种水头之间的转化关系,以及运动速度和压强随边界条件的变化关系。
实验目的
1
1.验证伯努力能量方程,加深对方程的理解;
2.学会各种水头的测试和计量方法;
3.观察并理解毕托管测速方法的原理。
实验原理
2
水流质点在流动的过程中具有位置高度,压力和速度,也就是说水流质点在流动的过程中具有位能、压能和动能,这三种能量可用水柱高表示。对于不可压缩理想液体(不存在粘滞性,液体的内摩擦力为零,故所做的功也为零)来说,水流质点从第一断面流向第二段面时这三种能量的变化关系可用伯努利方程表示:
因水流质点从一点流向另一点的过程中要消耗能量,降低水头,因此实际流体的水头线应是一条倾斜的曲线。
仪器结构
3

伯努利方程实验仪主要由恒水位木箱、伯努利方程实验管、测压管、蓄水箱、离心泵供水系统和电测流量装置等组成。恒水箱靠溢流来维持其恒定的水位,在水箱左下部装接水平放置的伯努利方程实验管,恒水位水箱中的水可经过伯努利方程实验管以恒定流流出,并可通过出水阀门调节其出水量。恒定流以一定流量流经试验管道时,通过安装在实验管的截面上的测压管(8 根),可以观测到相应截面上的水位值,从而可以分析管道中的稳定液流的各种能量形式、大小及其相互转化规律。
实验时,为了测定恒定流的流量,在出水端装有回水箱和计量水箱。用体积法测流量(量筒测量体积,秒表计时)。
伯努利方程试验管上的每个测量截面上的一组测压管,具有相当于毕托管的结构组成,所以,通过该实验装置,也可以进行毕托管测流速的实验。
实验步骤
4
1.实验前的准备
(1)关闭出水阀门。
(2)打开进水阀门,按下流量显示仪上的水泵开关,启动水泵,向恒水位水箱上水。
(3)在水箱接近放满时,调节阀门,使恒水位水箱达到溢流水平,并保持有一定的溢流。
(4)适度打开出水阀门,使伯努利方程试验管出流,此时,恒水位水箱仍能保持恒水位,且还有一定的溢流。否则,应调节进水阀门,使其达到恒水位并有适当溢流。(整个实验过程中都应满足这个要求)。
(5)实验测试之前,在作上述准备工作的过程中,应排尽管路和测压管中的空气。
(6)测试前,应仔细检查并调节电测流装置,使其能够正常工作。
2.进行测试
具体步骤如下:
(1).阀门开到大、小、中,稳定,观测各测压管读数,测量流量,记录数据。这里的三中状态均应该保持测压管中有数据可读(即有压流动状态);
(2).选择一次大流量情况下,绘制测压管水头线和总水头线。将以上测试数据记入实验记录下表:
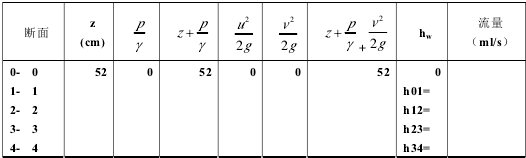
说明:各测量截面上的两个测压管,一个测压管测定的是相应截面的总水头,另一个测压管测定的是同一截面上的测压管水头,把这些实验数据直接记入实验记录表相应的栏中。在表中还应记录各工况的液体流量、试验管路的内径和位置水头。
数据整理及思考题
5
1.伯努利方程实验
(1)在测试所得实验数据基础上,计算出伯努利方程试验管各测试截面的相应流速水头和压强水头:
流速水头:
压强水头:
(2)绘制一定工况下的四个测试截面的各种水头和总水头的水
头线。
(3)运用伯努利方程进行分析,解释各水头的变化规律,例如:
①可以看出能量损失沿着流体流动的方向是增大的;
②2 截面和 1 截面,其位置水头相同,但 2 比 1 的压强水头大,这是由于管径变粗,流速减慢,流速水头转变为压强水头;
③3 截面与 2 截面比较,其位置水头相同,而 3 的压强水头小了,这是压强水头转变为流速水头了;
④4 截面与 3 截面比较,两管径相同,流速水头基本相同,但 4的压强水头比 3 的压强水头增大了,这是由于位置水头转变为压强水头了;
⑤实验结果还验证了连续方程,对于不可压缩流体的稳定流动,当流量一定时,管径粗的地方流速小,细的地方流速大。
2.测速实验
能量方程实验管上四组测压管的任一组都相当于一个毕托管,可测得管内的流体速度。由于本实验台将总水头测压管置于能量方程实验管的轴线,所以测得的动压头代表了轴心处的最大流速。
皮托管求点速度公式为:
此处, ∆h 为相应截面上两侧压管的水头差(即流速水头)。而管内的平均流速可以通过流量来确定,平均流速公式为:
在进行能量方程实验的同时,就可以测定出各点的轴心速度和平均速度。测试结果可记入下表 。