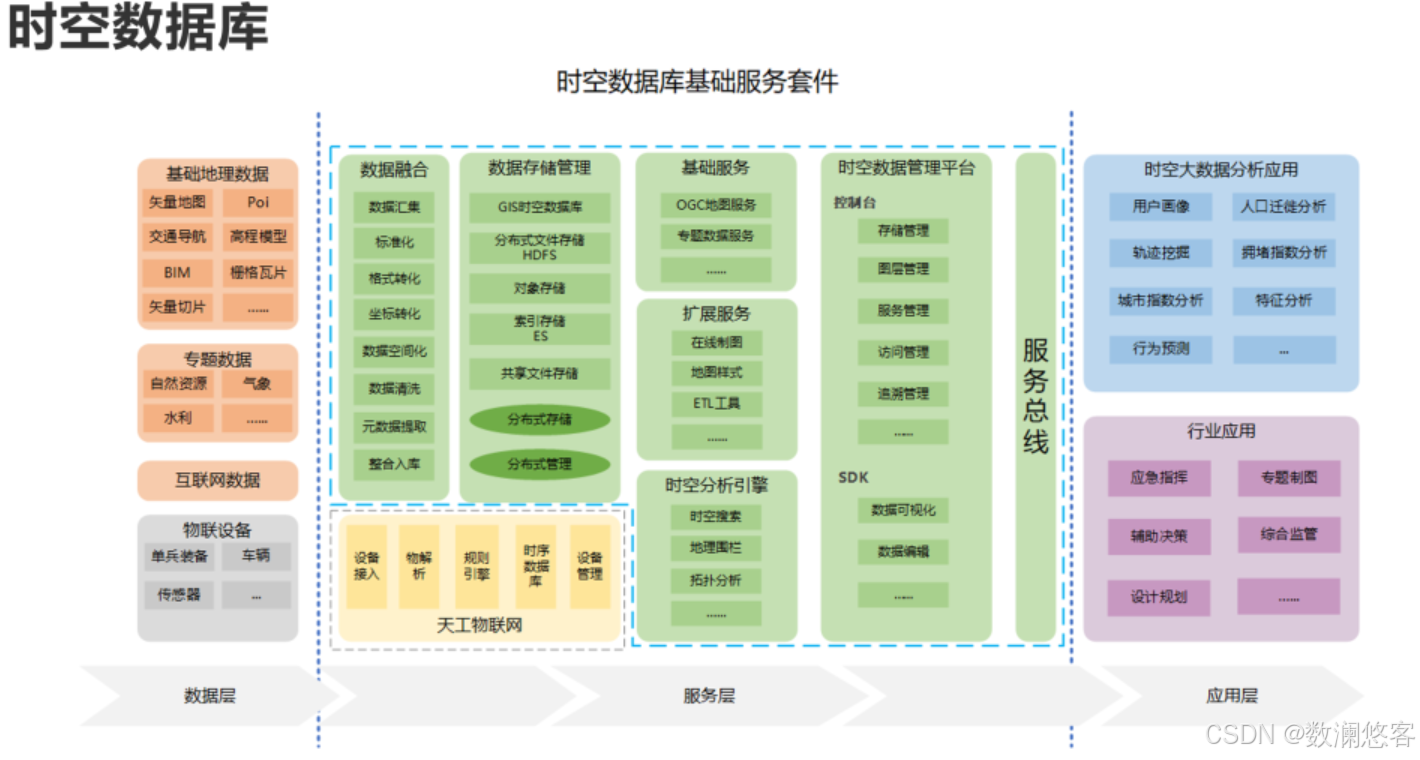
PyTorch学习(1)：张量（Tensor）核心操作详解

article/2025/8/6 7:46:40

PyTorch学习(1)：张量（Tensor）核心操作详解

一、张量（Tensor）核心操作详解

张量是PyTorch的基础数据结构，类似于NumPy的ndarray，但支持GPU加速和自动微分。

1. 张量创建与基础属性
import torch# 创建张量
a = torch.tensor([1, 2, 3])  # 从列表中创建
print(a)
b = torch.zeros(2, 3)   # 2*3零矩阵
print(b)
c = torch.ones_like(b)   # 与b同形的全1矩阵
print(c)
d = torch.rand(3, 4)  # 3*4随机矩阵
print(d)
e = torch.arange(0, 10, 2)  # [0,2,4,6,8]
print(e)# 关键属性查看
print(f"形状: {d.shape}")  # torch.Size([3, 4])
print(f"数据类型：{d.dtype}")  # torch.float32
print(f"存储设备: {d.device}") # cpu 或 cuda:0

2. 张量运算与广播机制
x = torch.tensor([[1, 2], [3, 4]])
y = torch.tensor([[5], [6]])
print(x)
print(y)# 基本计算
add =x + y   # 广播加法：[[6,7], [9,10]]
mul =x * 2   # 标量乘法：[[2,4], [6,8]]
print(add)
print(mul)# 高级运算
sum_x =torch.sum(x,dim=0)  # 沿列求和：[4,6]
max_val,max_idx=torch.max(x,dim=1) # 每行最大值和索引
exp_x =torch.exp(x)  # 指数运算
print(sum_x)
print(max_val,max_idx)
print(exp_x)

3. 形状操作与内存管理
z = torch.arange(12)
print(z)# 形状变换(不复制数据)
z_view =z.view(3,4)  # 视图变形,3*4矩阵
print(z_view)
z_reshape = z.reshape(2,6)
print(z_reshape)# 内部复制
z_clone = z.clone()  # 显性复制数据
z_transpone =z_view.T # 转置(共享数据)
print(z_clone)
print(z_transpone)# 维度操作
print(f"原始形状：{z.shape}")
unsqueezed = z.unsqueeze(0) # 增加维度：形状从(12,)变成(1,12)
print(f"增加维度后的形状：{unsqueezed.shape}")
print(unsqueezed)squeezed = unsqueezed.squeeze(0) # 压缩维度：shape(12)
print(f"压缩维度后的形状：{squeezed.shape}")

4. 与NumPy互操作
import numpy as np# Tensor → NumPy
tensor = torch.rand(2,3)
print (tensor)
numpy_array = tensor.numpy() # 共享内存（CPU张量）
print (numpy_array)# NumPy → Tensor
np_arr = np.array([[1,2],[3,4]])
print (np_arr)
new_tensor = torch.from_numpy(np_arr)  # 共享内存
print (new_tensor)# 显式内存复制
safe_tensor = torch.tensor(np_arr)
print (safe_tensor)

5、检查设备

# 检测GPU可用性
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")

二、动态计算图与自动微分（Autograd）

1. 计算图基本原理

PyTorch使用动态计算图，运算时实时构建计算图，示例1：

# 创建需要跟踪梯度的张量
x = torch.tensor(2.0,requires_grad=True)
print(x)# 定义一个简单的函数 y = x^2
y = x ** 2# 计算 y 关于 x 的梯度
y.backward()  # 执行反向传播# 查看梯度值 dy/dx = 2x = 2*2 = 4
print(x.grad)  # 输出: tensor(4.)

  1. torch.tensor(2.0)
    创建一个值为 2.0 的标量张量（即单元素张量），数据类型默认是torch.float32。

  2. requires_grad=True
    这是一个关键参数，它告诉 PyTorch 需要跟踪这个张量的所有操作，以便之后进行自动求导。设置为True后，PyTorch 会构建一个计算图，记录所有依赖于x的操作，从而在需要时通过反向传播（backpropagation）自动计算梯度。

在这个例子中，由于x的requires_grad=True，PyTorch 记录了y = x²的计算过程，并在调用y.backward()时自动计算了梯度dy/dx，结果存储在x.grad中。

为什么需要这样做？

在深度学习中，梯度是优化模型参数的关键。例如，在神经网络训练时，我们需要计算损失函数对模型参数的梯度，以便使用梯度下降等优化算法更新参数。通过将requires_grad设置为True，PyTorch 会自动记录所有对该张量的操作，从而在调用backward()方法时计算梯度。

这种自动计算梯度的能力是深度学习框架（如 PyTorch、TensorFlow）的核心优势之一，它让我们无需手动推导复杂模型的导数公式，就能高效训练神经网络。

PyTorch使用动态计算图，运算时实时构建计算图，示例2：

# 创建需要跟踪梯度的张量
x = torch.tensor(2.0, requires_grad=True)
# 定义一个函数 y = x**3 + 2*x + 1
y = x**3 + 2*x + 1
# 再进行函数
z = torch.sin(y)z.backward()  # 反向传播自动计算梯度print(x.grad)  # dz/dx = dz/dy * dy/dx = cos(y)*(3x²+2)

2. 梯度计算模式

这是更灵活的显式梯度计算方式，适用于复杂场景

# 示例：计算偏导数
u = torch.tensor(1.0, requires_grad=True)
v = torch.tensor(2.0, requires_grad=True)
f = u**2 + 3*v# 计算梯度
grads = torch.autograd.grad(f, [u, v])  # (df/du, df/dv)
print(grads)  # (tensor(2.), tensor(3.))
  • requires_grad=True 告诉 PyTorch 跟踪这些张量的所有操作，以便后续计算梯度。
  • \(u = 1.0\) 和 \(v = 2.0\) 是初始值，用于计算梯度的具体数值。

定义了一个二元函数 \(f(u, v) = u^2 + 3v\)。在深度学习中，这类似一个损失函数，我们需要计算它对参数的梯度。


 

核心区别
操作用途结果存储适用场景
z.backward()计算 z 对所有 requires_grad=True 的叶子节点张量的梯度，并累积到 .grad 属性中。梯度存储在叶子节点的 .grad 属性中。标准的反向传播（如训练神经网络）。
torch.autograd.grad(f, [u, v])显式计算 f 对指定张量 [u, v] 的梯度，返回梯度张量组成的元组。梯度作为元组直接返回，不修改原有张量。需要自定义梯度计算路径（如多输出模型）
3. 梯度控制技巧
import torch
import torch.optim as optim# 初始化参数
x = torch.tensor(2.0, requires_grad=True)
w = torch.tensor(3.0, requires_grad=True)
b = torch.tensor(1.0, requires_grad=True)# 创建优化器
optimizer = optim.SGD([x, w, b], lr=0.01)# 1. 梯度累积清零
optimizer.zero_grad()  # 训练循环中必须的操作
print(f"初始梯度 x.grad: {x.grad}")  # 输出: None# 前向传播
y = x * w + b
loss = (y - 10)**2  # 假设目标值为10# 反向传播
loss.backward()
print(f"第一次反向传播后 x.grad: {x.grad}")  # 输出: tensor(12.)# 再次反向传播（梯度会累积）
loss.backward()
print(f"第二次反向传播后 x.grad: {x.grad}")  # 输出: tensor(24.)# 梯度清零
optimizer.zero_grad()
print(f"optimizer.zero_grad() 后 x.grad: {x.grad}")  # 输出: tensor(0.)# 2. 冻结梯度
with torch.no_grad():z = x * 2  # 不会追踪计算历史
print(f"z.requires_grad: {z.requires_grad}")  # 输出: False# 3. 分离计算图
a = x * w
detached = a.detach()  # 创建无梯度关联的副本
print(f"detached.requires_grad: {detached.requires_grad}")  # 输出: False# 4. 修改requires_grad
x.requires_grad_(False)  # 关闭梯度追踪
print(f"修改后 x.requires_grad: {x.requires_grad}")  # 输出: False# 验证修改后的效果
try:y = x ** 2y.backward()  # 会报错，因为x.requires_grad=False
except RuntimeError as e:print(f"错误: {e}")  # 输出: element 0 of tensors does not require grad and does not have a grad_fn
总结对比表

optimizer.zero_grad()  # 训练循环中必须的操作
torch.no_grad() # 梯度清零
操作作用范围是否影响原张量是否释放内存典型场景
optimizer.zero_grad()优化器管理的所有参数是（梯度清零）否每个训练迭代前
torch.no_grad()上下文内的所有计算否是推理阶段、无需梯度的计算
a.detach()单个张量否（创建新张量）否截断梯度流、固定部分网络
x.requires_grad_(False)单个张量是（原地修改）否冻结预训练模型参数
代码说明：

  1. 梯度累积清零：

    • 两次调用 loss.backward() 会累积梯度
    • optimizer.zero_grad() 将梯度重置为零

  2. 冻结梯度：

    • with torch.no_grad() 块内的计算不会追踪梯度
    • 输出张量 z 的 requires_grad 为 False

  3. 分离计算图：

    • a.detach() 创建与计算图分离的新张量
    • 修改分离后的张量不会影响原梯度计算

  4. 修改 requires_grad：

    • x.requires_grad_(False) 原地修改张量属性
    • 后续尝试对 x 进行反向传播会报错
注意事项：
  • 实际训练中，optimizer.zero_grad() 应在每个训练迭代开始时调用
  • torch.no_grad() 常用于推理阶段以提高性能
  • detach() 适用于需要固定部分网络参数的场景
  • 修改 requires_grad 是永久性的，需谨慎操作
4. 梯度检查（调试技巧）
import torch
def grad_check():x = torch.tensor(3.0, requires_grad=True)y = x ** 2# 理论梯度y.backward()analytic_grad = x.grad.item()# 数值梯度（修正：使用 x.item() 而非硬编码 3.0）eps = 1e-5y1 = (x.item() + eps) ** 2y2 = (x.item() - eps) ** 2numeric_grad = (y1 - y2) / (2 * eps)print(f"解析梯度: {analytic_grad:.6f}, 数值梯度: {numeric_grad:.6f}")assert abs(analytic_grad - numeric_grad) < 1e-6# 调用函数
grad_check()

这段代码实现了一个简单的 ** 梯度验证（Gradient Check）** 功能，用于验证 PyTorch 自动微分计算的梯度是否与数值计算的梯度一致。

1. 定义测试函数和输入
x = torch.tensor(3.0, requires_grad=True)
y = x ** 2
2. 计算解析梯度（Analytical Gradient）
y.backward()
analytic_grad = x.grad.item()

3. 计算数值梯度（Numerical Gradient）
eps = 1e-5
y1 = (x.item() + eps) ** 2
y2 = (x.item() - eps) ** 2
numeric_grad = (y1 - y2) / (2 * eps)

4. 验证结果

print(f"解析梯度: {analytic_grad:.6f}, 数值梯度: {numeric_grad:.6f}")
assert abs(analytic_grad - numeric_grad) < 1e-6

打印结果：解析梯度: 6.000000, 数值梯度: 6.000000

关键知识点

  1. 自动微分（Autograd）： PyTorch 通过跟踪计算图自动计算梯度，无需手动推导公式。

  2. 数值微分： 数值方法是验证梯度计算正确性的重要工具，但计算效率低，仅用于测试。

  3. 梯度验证的重要性： 在实现复杂模型（如自定义层或损失函数）时，梯度验证能帮助发现反向传播中的错误。

潜在问题与改进

  1. 步长 \(\epsilon\) 的选择： 太小会导致数值误差（如浮点数舍入），太大会降低近似精度。

  2. 多维张量支持： 当前代码仅支持标量输入，扩展到多维张量需为每个元素计算数值梯度。

  3. 高阶导数验证： 对于二阶或更高阶导数，需使用更复杂的数值方法。

这个简单的验证函数是深度学习开发中的重要调试工具，特别是在实现自定义操作或优化算法时。


http://www.hkcw.cn/article/GnrBmHyOxk.shtml

相关文章

农村土地承包经营权二轮延包—生成地块的KJZB字段

农村土地承包经营权二轮延包—生成地块的KJZB字段

"关于地块的空间坐标&#xff08;KJZB&#xff09;字段&#xff0c;可能稍微复杂一点&#xff0c;用脚本生成较好。空间坐标&#xff0c;目前有两种表达&#xff1a;方案一&#xff0c;根据地块上界址点的个数依次填上&#xff08;如4个为J1/J2/J3/J4&#xff09;&#xf…
阅读更多...
时空数据智能分析的原理和案例分享

时空数据智能分析的原理和案例分享

在当今数字化时代，时空数据如同隐藏在海量信息中的宝藏，蕴含着丰富的价值，等待我们去挖掘和利用。从城市交通的实时监测与优化，到自然灾害的预警与防范，从精准农业的智能管理，到金融市场的动态分析，时空数据的身影无处不在，深刻地影响着我们生活的方方面面。DeepSeek，…
阅读更多...
专场回顾 | 重新定义交互，智能硬件的未来设计

专场回顾 | 重新定义交互，智能硬件的未来设计

自2022年起&#xff0c;中国智能硬件行业呈现出蓬勃发展的态势&#xff0c;市场规模不断扩大。一个多月前&#xff0c;“小智AI”在短视频平台的爆火将智能硬件带向了大众视野&#xff0c;也意味着智能硬件已不再仅仅停留在概念和技术层面&#xff0c;而是加速迈向实际落地应用…
阅读更多...
解决访问网站提示“405 很抱歉，由于您访问的URL有可能对网站造成安全威胁，您的访问被阻断”问题

解决访问网站提示“405 很抱歉，由于您访问的URL有可能对网站造成安全威胁，您的访问被阻断”问题

一、问题描述 本来前几天都可以正常访问的网站&#xff0c;但是今天当我们访问网站的时候会显示“405 很抱歉&#xff0c;由于您访问的URL有可能对网站造成安全威胁&#xff0c;您的访问被阻断。您的请求ID是&#xff1a;XXXX”&#xff0c;而不能正常的访问网站&#xff0c;如…
阅读更多...
十二、【核心功能篇】测试用例列表与搜索：高效展示和查找海量用例

十二、【核心功能篇】测试用例列表与搜索：高效展示和查找海量用例

【核心功能篇】测试用例列表与搜索&#xff1a;高效展示和查找海量用例 前言准备工作第一步&#xff1a;更新 API 服务以支持分页和更完善的搜索第二步&#xff1a;创建测试用例列表页面组件 (src/views/testcase/TestCaseListView.vue)第三步&#xff1a;测试列表、搜索、筛选…
阅读更多...
Windows环境下PHP，在PowerShell控制台输出中文乱码

Windows环境下PHP，在PowerShell控制台输出中文乱码

解决方法&#xff1a; 以管理员运行PowerShell , 输入&#xff1a; chcp 65001 重启控制台&#xff1b;然后就正常输出中文&#xff1b;
阅读更多...
安卓apk安装包签名步骤

安卓apk安装包签名步骤

1.获取apk对应的原始证书&#xff08;问前端要&#xff09; 2.打开命令窗口win r 输入 cmd 3.输入 cd .android 定位到 .android 文件夹 4.执行证书签名命令 keytool -genkey -v -keystore 前端提供的.keystore -alias 自定义别名信息 -keyalg RSA -validity 10000 密钥为&a…
阅读更多...
C与C++相互调用

C与C++相互调用

C与C为什么相互调用的方式不同 C 和 C 之间的相互调用方式存在区别&#xff0c;主要是由于 C 和 C 语言本身的设计和特性不同。 函数调用和参数传递方式不同 &#xff1a; C 和 C 在函数调用和参数传递方面有一些不同之处。 C 使用标准 的函数调用约定&#xff0c;而 …
阅读更多...
Nest全栈到失业(附加):Mysql+TypeOrm构建CRUD

Nest全栈到失业(附加):Mysql+TypeOrm构建CRUD

前置内容 在此之前,我希望你准备好一个docker环境,以及魔法的网络哦 自己创建一个项目哈,使用nest new XXX Docker 什么是docker?相信很多人都知道了,说白了,就是一个镜像容器;以mysql为例,你在电脑上使用mysql5.6啥的,他电脑上是5.7啥的,然后数据内容不兼容了,怎么办了?他卸…
阅读更多...
InnoDB引擎逻辑存储结构及架构

InnoDB引擎逻辑存储结构及架构

简化理解版 想象 InnoDB 是一个高效运转的仓库&#xff1a; 核心内存区 (大脑 & 高速缓存 - 干活超快的地方) 缓冲池 Buffer Pool (最最核心&#xff01;)&#xff1a; 作用&#xff1a; 相当于仓库的“高频货架”。把最常用的数据&#xff08;表数据、索引&#xff09;从…
阅读更多...
基于定制开发开源AI智能名片S2B2C商城小程序的大零售渗透策略研究

基于定制开发开源AI智能名片S2B2C商城小程序的大零售渗透策略研究

摘要&#xff1a;本文聚焦“一切皆零售”理念下的大零售渗透趋势&#xff0c;提出以定制开发开源AI智能名片S2B2C商城小程序为核心工具的渗透策略。通过分析该小程序在需求感应、场景融合、数据驱动等方面的技术优势&#xff0c;结合零售渗透率提升的关键路径&#xff0c;揭示其…
阅读更多...
基于SpringBoot的在线拍卖系统计与实现(源码+文档+部署讲解）

基于SpringBoot的在线拍卖系统计与实现(源码+文档+部署讲解）

技术范围&#xff1a;SpringBoot、Vue、SSM、HLMT、Jsp、PHP、Nodejs、Python、爬虫、数据可视化、小程序、安卓app、大数据、物联网、机器学习等设计与开发。 主要内容&#xff1a;免费功能设计、开题报告、任务书、中期检查PPT、系统功能实现、代码编写、论文编写和辅导、论文…
阅读更多...
二分法算法技巧-思维提升

二分法算法技巧-思维提升

背景&#xff1a; 在写力扣题目“搜素插入位置 ”时&#xff0c;发现二分法的一个细节点&#xff0c;打算记录下来&#xff0c;先看一张图&#xff1a; 我们知道&#xff0c;排序数组&#xff0c;更高效的是二分查找法~~~而二分法就是切割中间&#xff0c;定义left是最开始的&…
阅读更多...
实验分享|基于sCMOS相机科学成像技术的耐高温航空涂层材料损伤检测实验

实验分享|基于sCMOS相机科学成像技术的耐高温航空涂层材料损伤检测实验

1实验背景 航空发动机外壳的耐高温涂层材料在长期高温、高压工况下易产生微小损伤与裂纹&#xff0c;可能导致严重安全隐患。传统光学检测手段受限于分辨率与灵敏度&#xff0c;难以捕捉微米级缺陷&#xff0c;且检测效率低下。 某高校航空材料实验室&#xff0c;采用科学相机…
阅读更多...
特伦斯 S75 电钢琴：重构演奏美学的极致表达

特伦斯 S75 电钢琴：重构演奏美学的极致表达

在数字音乐时代&#xff0c;电钢琴正从功能性乐器升级为融合艺术、科技与生活的美学载体。特伦斯 S75 电钢琴以极简主义哲学重构产品设计&#xff0c;将专业级演奏体验与现代家居美学深度融合&#xff0c;为音乐爱好者打造跨越技术边界的沉浸式艺术空间。 一、极简主义的视觉叙…
阅读更多...
室内VR全景助力房产营销及装修

室内VR全景助力房产营销及装修

在当今的地产行业&#xff0c;VR全景已成为不可或缺的应用工具。从地产直播到楼市VR地图&#xff0c;从效果图到水电家装施工记录&#xff0c;整个地产行业的上下游生态中&#xff0c;云VR全景的身影无处不在。本文将探讨VR全景在房产营销及装修领域的应用&#xff0c;并介绍众…
阅读更多...
AWS API Gateway 配置WAF（中国区）

AWS API Gateway 配置WAF（中国区）

问题 需要给AWS API Gateway配置WAF。 AWS WAF设置 打开AWS WAF首页&#xff0c;开始创建和配置WAF&#xff0c;如下图&#xff1a; 设置web acl名称&#xff0c;然后开始添加aws相关资源&#xff0c;如下图&#xff1a; 选择资源类型&#xff0c;但是&#xff0c;我这里出…
阅读更多...
文件雕刻——一种碎片文件的恢复方法

文件雕刻——一种碎片文件的恢复方法

文件雕刻是指基于对文件格式而非其他元数据的了解&#xff0c;在数据流中搜索文件的一种过程。 当文件系统元数据损坏或无法使用时&#xff0c;雕刻非常有用。FAT 文件系统&#xff08;通常用于小型介质&#xff09;是最常见的例子。 删除文件或格式化介质后&#xff0c;文件系…
阅读更多...
如何解决MySQL Workbench中的错误Error Code: 1175

如何解决MySQL Workbench中的错误Error Code: 1175

错误描述&#xff1a; 在MySQL Workbench8.0中练习SQL语句时&#xff0c;执行一条update语句&#xff0c;总是提示如下错误&#xff1a; Error Code: 1175. You are using safe update mode and you tried to update a table without a WHERE that uses a KEY columnTo disab…
阅读更多...
VScode-使用技巧-持续更新

VScode-使用技巧-持续更新

一、Visual Studio Code - MACOS版本 复制当前行 shiftoption方向键⬇️ 同时复制多行 shiftoption 批量替换换行 在查找和替换面板中&#xff0c;你会看到一个 .∗ 图标&#xff08;表示启用正则表达式&#xff09;。确保这个选项被选中&#xff0c;因为我们需要使用正则…
阅读更多...
推荐文章

Copyright @ 2022~2023