行程问题是小学数学应用题中的基本问题,它包含了简单的相遇及追及问题、多人相遇追及问题、多次相遇追及问题、流水行船问题、环形跑道问题、钟面行程问题、火车过桥问题、猎狗追兔问题等,但万变不离其宗。行程问题是物体匀速运动的应用题。不论是同向运动还是相向运动,最后反映出来的基本关系式都可以归纳为路程=速度×时间。
要想解答行程问题,首先要弄清物体的具体运动情况,可以在纸上画出相应的运动轨迹,更方便观察思考。

01
相遇问题
关键点:同时出发,相向而行或相对而行
基础的相遇问题
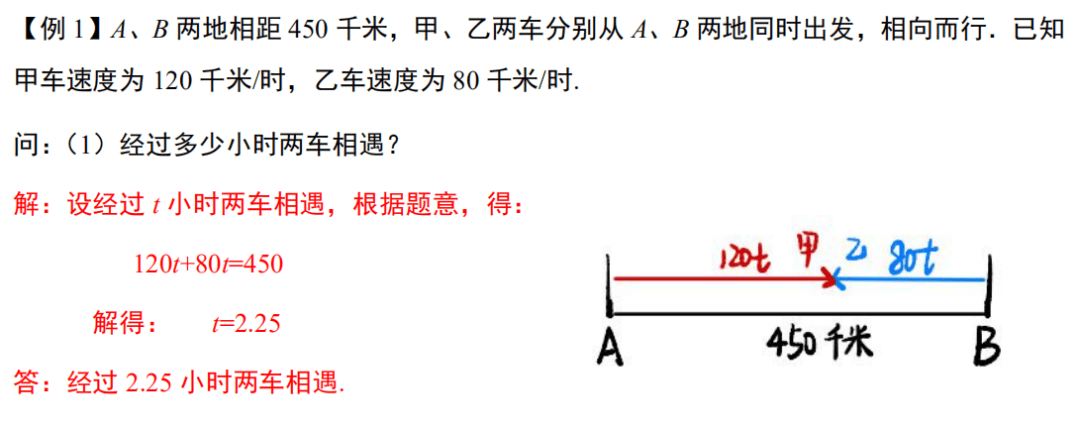
【分析】
1.两个人同时走,同时停,所用时间一样。
2.双方所走路程和=全部路程。
【总结】画出路程图,根据路程相等列出方程。
相遇问题中的相距问题
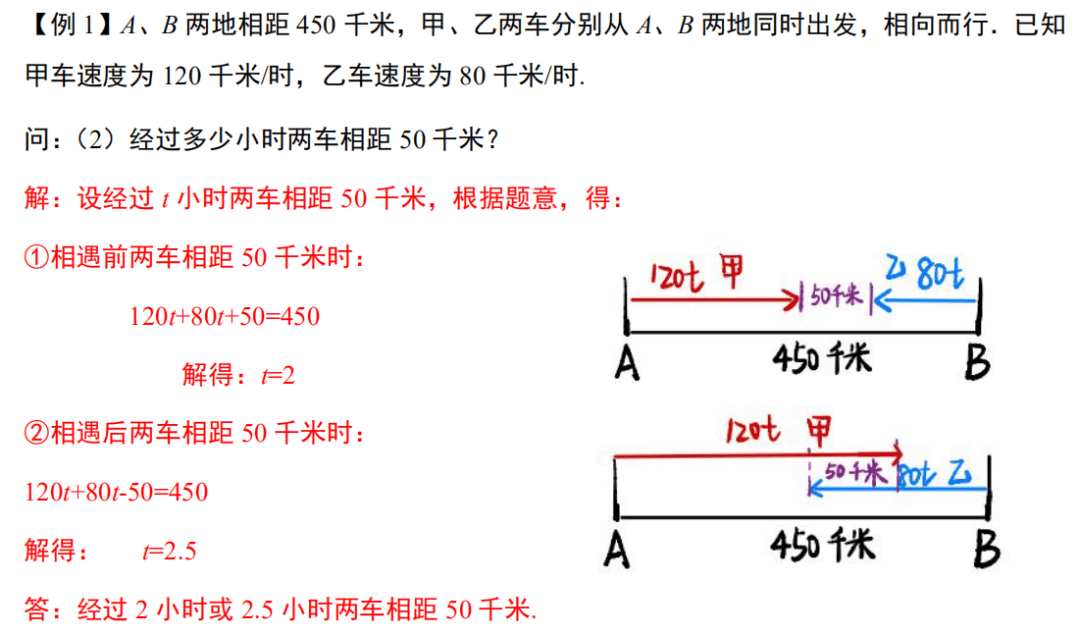
【分析】
这类问题需要注意分类讨论,分为相遇前相距和相遇后相距两种情况。
【总结】画出路程图,根据路程相等列出方程。
02
追及问题
基础的追及问题

【分析】
1.两个人同时朝一个方向走,同时停,所用时间一样。
2.根据相距路程+慢的路程=快的路程
【总结】画出路程图,根据路程相等列出方程。
追及问题中的相距问题
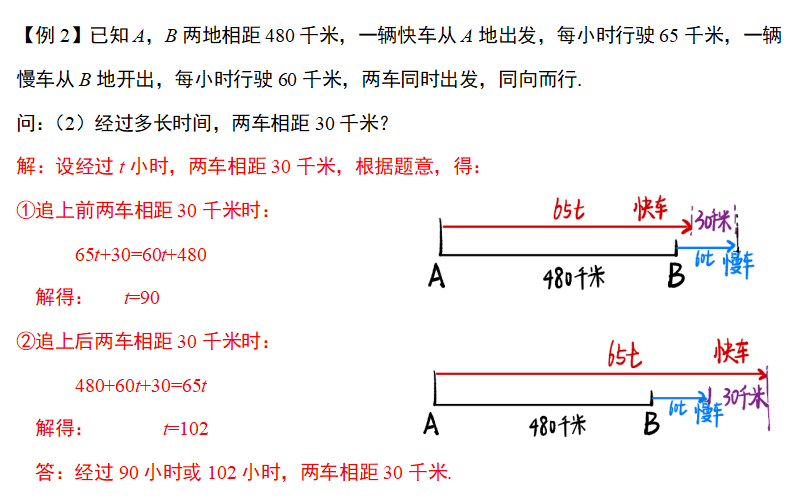
【分析】
这类问题需要注意分类讨论,分为追上前相距和追上后相距两种情况。
【总结】画出路程图,根据路程相等列出方程。
其实所有的行程问题都是围绕着“路程=速度×时间”(即s=v×t)这一基本关系式展开的,相遇与追及问题也不例外。这类题目虽然有时考查的较为复杂,但只要抓住这个基本的等量关系公式,画出相应的线段图,利用线段的和差表示路程的大小关系,很多问题就都迎刃而解了。
03
小试牛刀
1、A、B 两地间有条公路,甲从 A 地出发步行前往 B 地,乙骑摩托车从 B 地同时出发,不停顿地往返于 A、B 两地之间。80 分钟后他们第一次相遇,又过了 20 分钟乙第一次超越甲。求甲、乙速度之比。
2、甲、乙和丙三人同时分别由东西两城出发,甲乙两人由东城到西城丙由西城到东城。甲步行每小时行 5 千米,乙骑自行车每小时行 15 千米,丙骑自行车每小时行 20千米。已知丙在途中遇到乙后,又经过 1 小时后才遇到甲,问东西两城相距多少千米?
3、甲、乙两人分别从 A、B 两地同时出发相向而行,出发时他们的速度比为 3:2,他们第一次相遇后,甲的速度提高了 20%,乙的速度提高了 30%,这样,当甲到达 B 地时,乙离 A 地还有 14 千米,A、B 两地间的距离是多少千米?
4.宝强开车从 A 城市到 B 城市,从开始出发,车速即比原计划的速度提高了1/9,结果提前 1.5 小时到达;返回时,按原计划的速度行驶 280 千米后,将车速提高1/6,于是提前 1 小时 40 分钟到达 A 城市。求 A、B 两座城市之间的路程是多少千米?
běn
总
kè
结
bǐ
笔
jì
记
♥基本行程问题公式
路程=速度×时间
时间=路程÷速度
速度=路程÷时间
♥相遇与追及问题
·相遇问题
路程和=速度和×相遇时间
速度和=路程和÷相遇时间
相遇时间=路程和÷速度和
·追及问题
路程差=速度差×追及时间
速度差=路程差÷追及时间
追及时间=路程差÷速度差
·中点相遇问题
路程差等于相遇地点与中点距离的2倍
·复杂追及问题
注意找出隐藏路程差
·和差公式
大数=(和+差)÷2
小数=(和-差)÷2
♥火车行程问题
火车过桥(完全通过):路程=桥长+车长
火车过人:路程=车长
火车过火车:路程=车长+车长
♥流水行船问题
顺水速度=静水船速+水速
逆水速度=静水船速-水速
静水船速=(顺水速度+逆水速度)÷2
水速=(顺水速度-逆水速度)÷2
♥环形路线问题
同时同地背向:相遇1次,合走1圈;
同时同地同向:追及1次,多走1圈。
♥利用正、反比例解决行程问题
根据定值,寻找正、反比例关系;
设份,求出1份量;
再按比分配。
五年级下册数学常考重点公式默写 2024-05-29
四年级下册数学必背九大考点总结 2024-05-28
四年级数学下册十大易错题(附答案),来练习! 2024-05-27
小学数学/综合整理▍
综合整理自网络/声明▍
商务合作微信:JJYYshangwu
//
免责声明
1.本公众号部分转载的文章、图文、视频来自网络,其版权和文责属原作者所有,若来源标注错误或侵犯到您的权益,烦请告知,我们将立即删除。
2.本公众号编辑部工作人员的原创文章,其版权属于我们微信公众号所属主体。
3.本公众号特约稿原创文章,其版权和文责属作者所有。
4.若要转载原创文章用于商业用途,请联系我们,未经同意不得转载。任何转载请注明文章来源。如有问题,请联系我们,谢谢!