
点击上面“蓝字”关注我们
电源分配是支持所有类型硅产品运行的基础设施的重要组成部分,但在设计过程中常被忽视。电源质量可能限制电路性能,并决定其工作可靠性。要真正解决电源分配问题,必须考虑包括芯片、封装和PCB在内的整个系统。
芯片设计者通常关注直流压降,但系统无源分量(包括芯片电容以及封装和PCB结构的电感)通常比IR压降更具主导性。这些无源分量形成存储和释放特定频段能量的谐振结构。PDN谐振是系统的固有特性,无法通过单独分析芯片、封装或PCB来预测。必须从整体系统角度出发,才能预测频域中的谐振阻抗峰值以及时域中片上电路所经历的最小和最大电压。
电源分配网络理论
PDN设计的起点是目标阻抗。这是一个基于欧姆定律的简单计算,可有效指示需要多少芯片和封装资源(如片上电容、封装电容、引脚数量、过孔、电源平面尺寸等)才能以合理质量向片上电路供电。
图1展示了理想电压源通过阻抗连接至电路负载的示意图。负载电流通常随时间变化,具体取决于电路的当前操作。在较长时间尺度上,负载电流会因芯片处于省电模式、空闲状态或数据处理状态而发生功耗瞬变。当电流流经阻抗时,这些功耗瞬变会导致负载端电压波动。
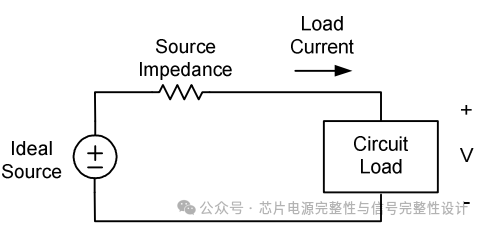
图1.通过电源阻抗连接至理想电压源的片上电路负载。负载电流的变化会导致电路端电源电压的变化。
为制定PDN设计准则,需设定一个足够低的目标阻抗,以最低成本提供高质量电源。该目标具有双重意义:若实际阻抗超过目标阻抗,电路可能面临故障风险;若实际阻抗低于目标阻抗,则可能造成不必要的成本增加。目标阻抗的定义为:
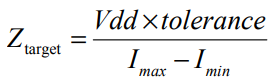
例如,标称电压为1.0伏的电源可能在5%的电压变化范围内正常工作。在典型操作中,IP开关活动可能导致最大7A电流消耗,或在空闲或省电模式下仅需2A。瞬态电流为最大与最小电流之差(本例中为5A)。
此时有必要讨论串联和并联配置中电感和电容无源分量的特性。图2展示了三个元件(100nF、4mΩ和120pH)的串联和并联电路示意图。从外部(封装引脚)看,元件为串联;但从硅电路视角看,片上电容与封装电感并联。通过矢量网络分析仪(VNA)可测量串联电路以确定封装内的无源参数(R、L、C)。当硅电路在系统中运行时,相同元件的并联拓扑结构将主导其连接方式。
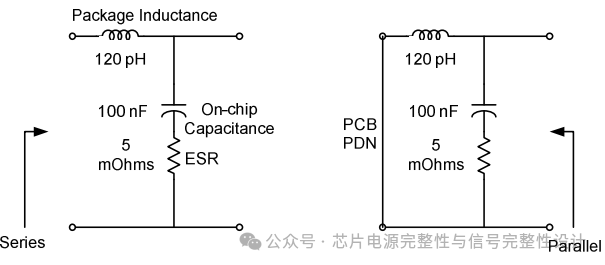
图2.代表Core逻辑PDN集总参数的RLC元件串联与并联电路。当封装芯片连接到低阻抗PCB PDN时,片上电路感知到的是并联电路。
图3展示了串联和并联电路的仿真结果。电感阻抗为jωL,电容阻抗为1/(jωC)。串联电路呈现阻抗凹陷,并联电路呈现阻抗峰值。电阻(等效串联电阻,ESR)的作用是定义串联电路的最小阻抗值,并决定并联电路的峰值高度。谐振频率始终为f_o=1/(2π√LC)。品质因数Q定义为谐振时的无源阻抗与电阻之比:Q=X/R=√L/C/R。并联谐振的峰值高度近似为XQ=X^2/R=(L/C)/R。
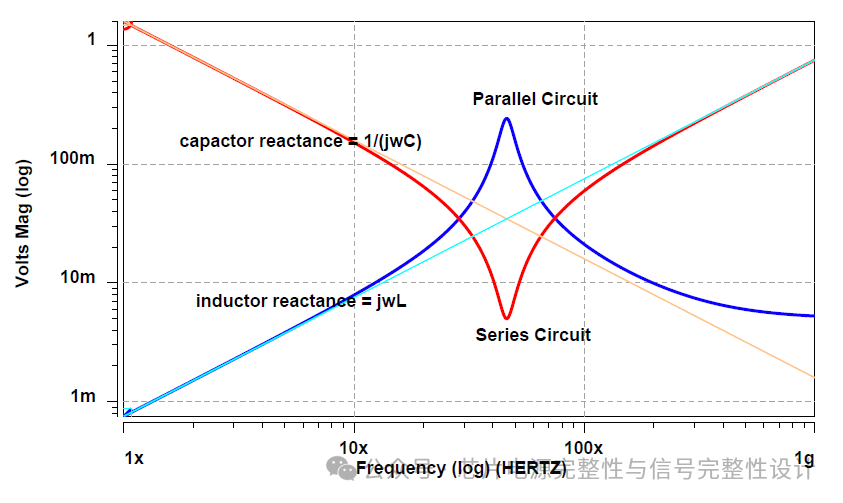
图3:基于图2串联和并联电路的仿真:ESR控制q因子,倾斜的深度和峰值的高度。
Core电源的典型PDN
实际PDN包含电容和电感无源分量,导致其阻抗在应用中不可忽视。图4展示了电源分配系统的多个组件的示意图及其频域阻抗(频率范围为kHz至GHz)。实际阻抗需与平坦目标阻抗对比。由于用户活动可能以任意时钟分频率激励PDN,因此需选择满足平坦目标阻抗的元件。不同频段的阻抗由特定电路参数主导,各元件大致位于其控制的频段下方。最显著的阻抗峰值出现在43MHz,由片上电容与PCB安装的封装电感谐振引起,称为芯片/封装谐振。
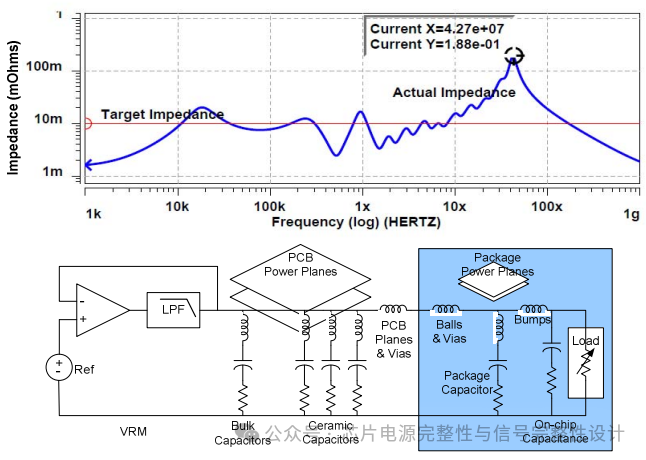
图4.PDN由控制不同频段阻抗的组件构成。典型Core逻辑PDN的阻抗曲线显示约43MHz处的峰值远超目标阻抗。
图5展示了相同PDN电路的时域仿真结果。负载根据上述目标阻抗计算绘制快速瞬态电流。功耗瞬变上升时间仅数纳秒,典型功耗瞬变可在几个时钟周期内发生,并根据阶跃函数的上升时间包含高频成分。约300MHz以下的频率峰值将被激励。本仿真中,43MHz的频域峰值导致时域中该频率的阻尼正弦振荡。需注意:功耗瞬变上升时伴随负向正弦波,下降时伴随正向正弦波。
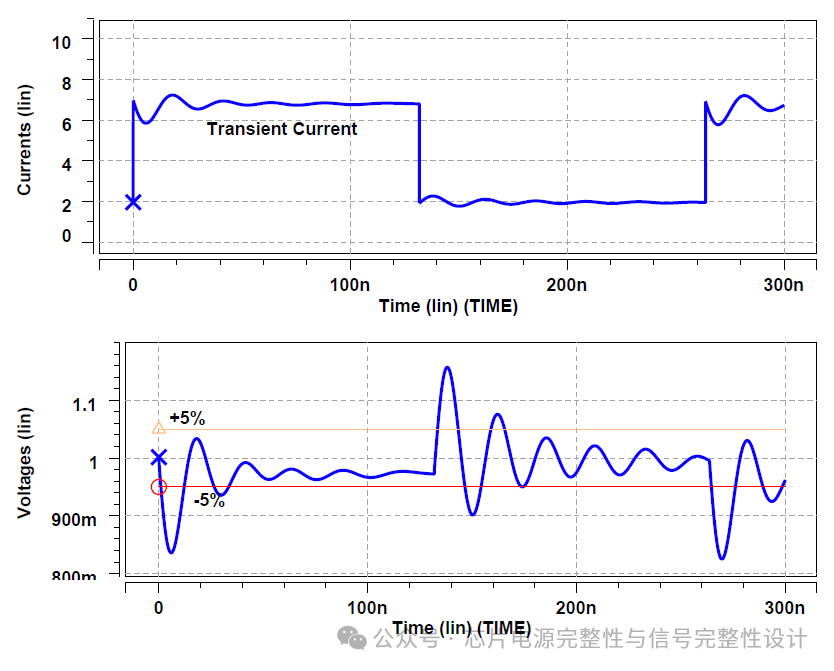
图5.片上负载从PDN汲取5A时域瞬态电流。片上电压随电流瞬变产生凹陷与峰值,并以PDN谐振频率呈现阻尼正弦振荡。
选择电阻性负载而非恒流源来表征CMOS电路。CMOS电路的电流消耗随电源电压升高而增加,随电压降低而减少,与电阻特性相似。恒流源无法正确反映电源电压变化对电流的影响,也无法提供适当的阻尼。因此,PDN负载采用时变电阻模型,导致非方波电流波形和功耗瞬变。
为清晰观察每个瞬变的影响,上升和下降功耗瞬变在时间上间隔开。但用户活动可能以任意时钟分频率随机激励PDN。图6展示了相同电路在极端激励频率(精确匹配43MHz谐振频率)下的仿真结果。功耗瞬变导致阻尼正弦波叠加,波形在多个周期内累积。标称电源电压为1.0伏时,仿真显示最大和最小电压偏移分别为1.39伏和0.59伏(实际电源容差达+40%),原因是实际阻抗远超目标阻抗。
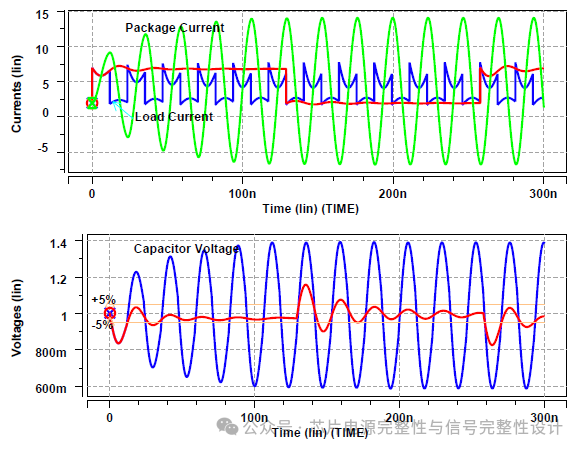
图6.IP工作产生的功耗瞬变以谐振频率激励PDN。由于实际阻抗超过目标阻抗,波形叠加并累积至远超电源容差限值。
并联谐振电路的峰值是PDN问题的根源。从上述公式可知,Q因数决定了谐振峰值的高度。电阻始终为并联谐振电路提供阻尼。电感增加会提高Q因数,电容增加则会降低Q因数。然而,增加片上电容和减少封装电感通常意味着更高成本。显然,PDN的成本与性能密切相关。
物理结构与电路参数
图7展示了物理系统的结构剖面。谐振结构的大部分电容位于芯片上。在良好去耦的PCB上,去耦电容形成的低交流阻抗可视为短路。芯片通过C4焊球连接至封装,封装通过焊球连接至PCB。封装和PCB内部均包含过孔和电源平面。电流从PCB电容通过电源平面、焊球、过孔和凸点形成环路,并通过地结构返回。该大环路具有环路电感。
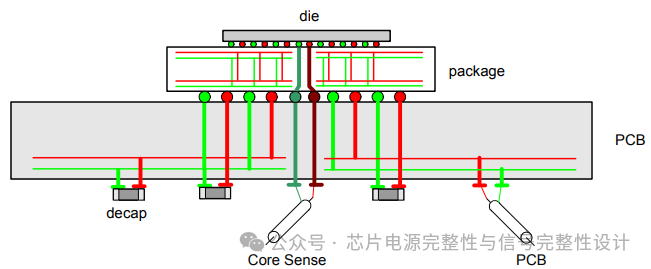
图7:芯片安装在封装和PCB上的截面。PCB去耦电容的电流回路由PCB电源平面、过孔、焊球、封装过孔和芯片焊点形成。该回路的每个部分都贡献了在芯片/封装谐振期间有效的电感。
片上PDN噪声测量
为实时监测片上电压噪声,测试芯片上实现了高带宽探针。如图7所示,一对封装焊球通过封装镀通孔(PTH)过孔和芯片凸点直接连接至片上电源和地网络。该探针与封装和PCB中的其他电源/地网络隔离,其阻抗和带宽(超过1GHz)经过严格控制。通过该专用探针测量片上电压噪声。
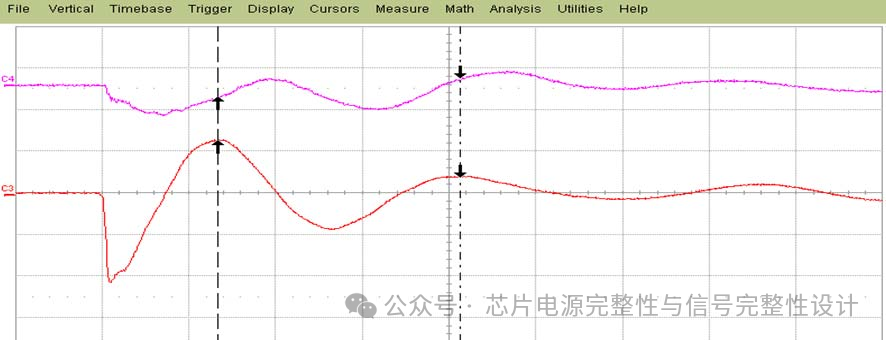
图8:测量的片上和PCB电压噪声。
图8展示了片上PDN电压噪声波形与PCB级PDN噪声的示波器截图。测试芯片上实现了约10万个T触发器(TFF),并触发一次切换。首次电压下降由TFF同步开关电流引起,电压凹陷为1.1V标称电压的105mV,下降沿小于500ps。对于此类快速开关事件,所有电流必须从物理邻近且低电感的片上电容汲取。电压突降后,PCB PDN通过封装和PCB电感向片上电容补充电荷。
后续峰值是电感过冲(67mV)。阻尼电压振荡由系统PDN谐振频率和Q因数决定。片上峰峰值电压噪声为172mV(占标称电压的16%),而PCB级峰峰值噪声仅11mV(1%)。实验表明,即使PCB级PDN噪声控制良好,芯片级PDN噪声仍可能显著更高。电路设计时必须考虑此类大幅电压波动。
模型与硬件相关性
片上PDN电压噪声由芯片电流消耗驱动。为理解其本质,定义了三个关键电流项:
1.时钟边沿电流
2.每时钟周期电荷量
3.动态电流

图9:片上电流定义的示意图
通过电流控制电阻模型精确建模片上电路负载。电流波形采用Gamma分布的概率密度函数(PDF)表示。对于测试芯片中的TFF电路,时钟边沿电流的上升时间和下降时间分别为400ps和900ps(通过电路时序分析和模型-硬件相关性验证)。表2总结了仿真与实测结果的电压凹陷、峰峰值和PDN谐振频率,差异在数个百分点内。所提负载模型实现了硬件测量与仿真的良好相关性。
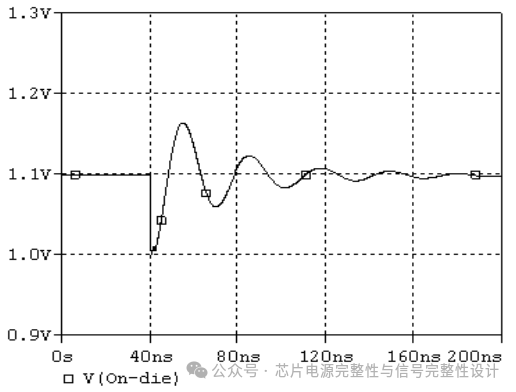
图10.单次开关事件下的片上PDN电压噪声仿真结果。
表2.仿真与实测片上电压噪声对比

PDN激励定义
前文表明,片上PDN噪声可能比PCB级高一个数量级。为确保PDN鲁棒性,需在系统使用场景下测量或仿真各类电流激励的片上电压。定义了三种基本激励以系统地表征片上PDN特性与电压噪声:脉冲激励、交流稳态激励和瞬态突发模式。
A.脉冲激励
冲激励通过单次触发电路开关产生脉冲电流,用于表征系统PDN的脉冲响应。图8展示了脉冲激励下的片上电压噪声波形。通过系统PDN脉冲响应可提取以下特性:
1.片上电压凹陷与过冲
2.根据第一和第二个谐振峰时间间隔计算系统PDN谐振频率(33MHz)
3.通过谐振峰数量估算Q因数(本例约为3)
B.交流稳态
交流稳态指电路在多时钟周期内重复开关,PDN电流/电压达到稳态。图11展示了不同时钟频率下的片上电压波形。当时钟频率等于PDN谐振频率(33MHz)时,片上电压噪声达到最大值(电路开关电流激励PDN谐振)。超过33MHz后,噪声幅度随频率指数下降,与图4的阻抗曲线一致。该系列波形中,工作台电源电流与时钟频率成正比。
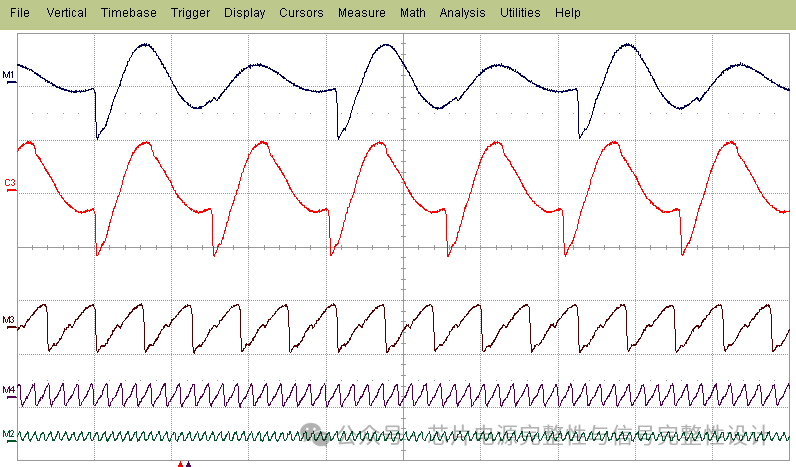
图11:在交流稳态刺激下,测量了不同时钟频率的片上电压噪声。动态电流与频率成正比。
C.突发模式
逻辑电路通常根据输入数据向量切换。为表征电路开关电流与系统PDN的相互作用,突发模式定义为空闲状态后的一连串电路切换。图12展示了突发激励下的片上PDN噪声。TFF的突发活动由时钟信号(图中第三曲线)控制。前10ns时钟保持低电平(无切换),随后266MHz时钟触发TFF切换并汲取电流。片上电压在前两次TFF切换时持续下降(仅片上电容供能),最大凹陷为137mV(标称电压的12.5%)。第三次切换后,封装和PCB开始向芯片供电,电压恢复。突发结束时的电流突变导致显著电感过冲(图12)。突发模式可用于表征片上电容的有效性和系统PDN响应时间。
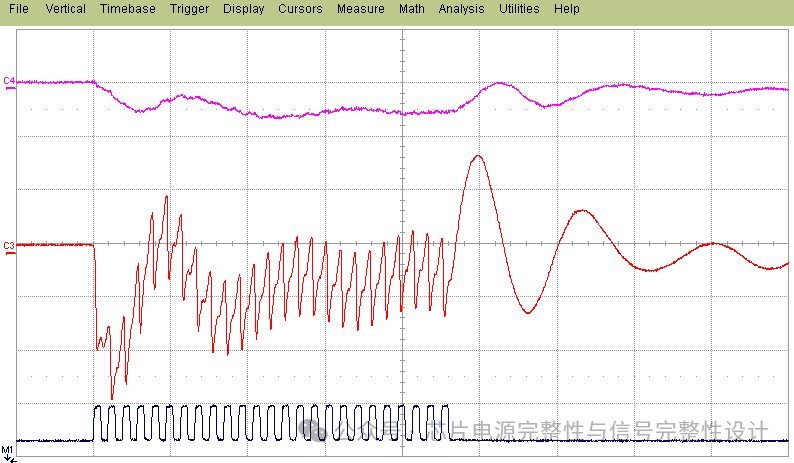
图12:用突发模式刺激测量片上电压噪声波形。
为评估PDN鲁棒性,定义了最坏情况激励。如图13第三曲线所示,周期性突发模式以PDN谐振频率重复,由于并联谐振特性,最大程度激励PDN并导致最强电压波动。本例中,533MHz突发时钟下,峰峰值电压达577mV(标称电压±26%)。实际设计中,逻辑电路难以实现完美的周期性突发同步切换。
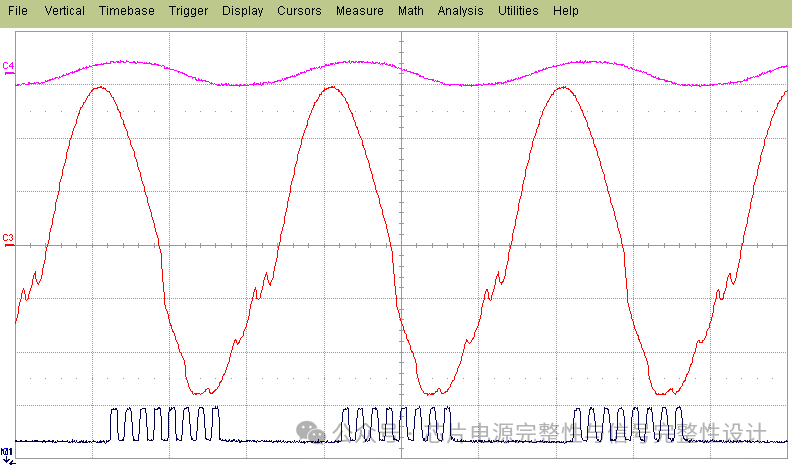
图13:用周期性突发模式刺激测量片上电压噪声波形。
图14.33MHz周期性突发激励下的芯片负载电流、封装电流和片上电容(ODC)电流仿真结果。高频电流由ODC提供,低频电流由PCB PDN通过封装提供。
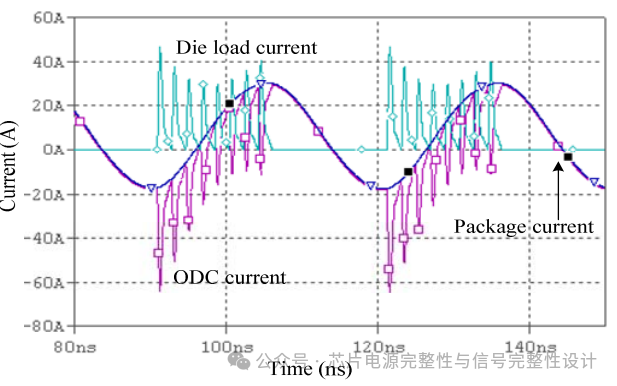
图14:仿真PDN谐振频率下周期性突发刺激下的芯片负载电流、封装电流和ODC电流。
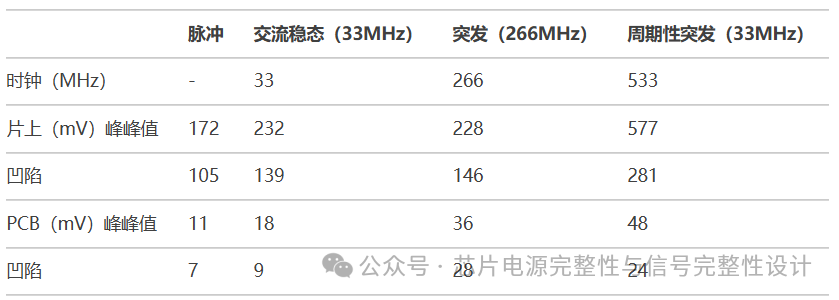
表3对比了不同激励下的电压噪声幅度。关键结论是:即使PCBPDN去耦良好,片上噪声仍显著更高。传统认为交流稳态激励是最坏情况,但实验证明并非如此。
表3.不同PDN激励下的片上与PCB电压噪声幅度
PRBS激励与PDN谐振
为模拟实际使用的随机性,采用PRBS信号作为TFF的时钟信号。PRBS的时钟上升沿间隔可变(如2T0和6T0),导致电路开关频率覆盖基础时钟的所有分频。PRBS全序列的开关频率谱可扩展至所有分频,最高频率为fclk/2,最低为fclk/(2^n-1)(n为PRBS序列长度)。图15展示了PRBS时域波形及其开关频率概率分布(非谐波幅度)。图16显示PRBS时钟驱动TFF时的片上电压噪声(峰峰值251mV)。当PRBS模式在30ns间隔(33MHz)重复时,PDN谐振被强烈激励。
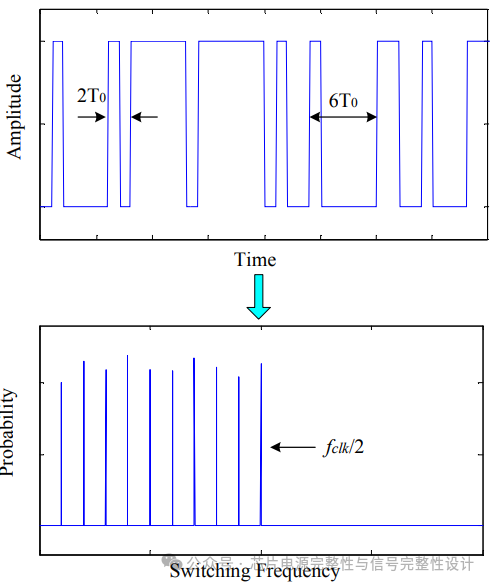
图15:当一个PRBS信号被用作时钟信号时,在时域内的PRBS波形和相应电路的开关频谱
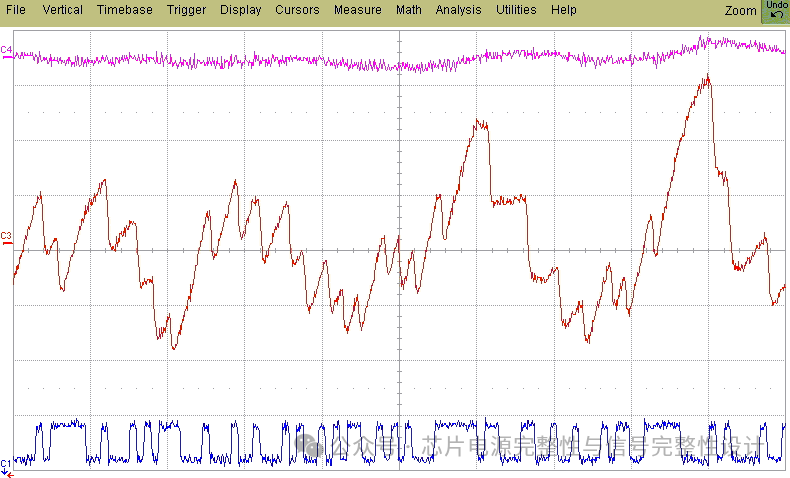
图16.PRBS时钟信号驱动TFF时的实测片上电压噪声。
时序与抖动影响
片上电压波动会缩小时序裕量,并可能因时序违例导致功能故障。为量化影响,将时钟网络作为受害对象。图17展示了脉冲激励下时钟周期抖动与片上电压噪声的关系。电压凹陷导致时钟周期因CMOS速度下降而延长,电压过冲则缩短周期。160mV电压波动导致169ps峰峰值抖动。时钟周期波形与电压噪声呈反向相关,清晰证明了二者的因果关系。
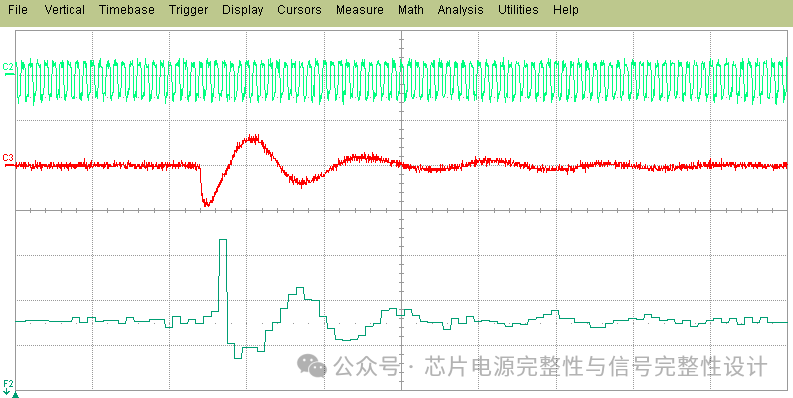
图17.脉冲激励下时钟周期抖动的实测结果(500MHz受害时钟)。
结论
PDN谐振导致的电源电压波动比直流IR压降更严重。根本原因是电感(磁场)与电容(电场)并联时的能量谐振。谐振频率和幅值由系统参数(包括板级/封装电感和芯片电容)决定。频域峰值对应时域阻尼正弦振荡,IP开关活动的叠加效应常导致电压容差超标。即使PCB去耦良好,片上瞬态噪声仍显著更高。通过三种基本激励可系统表征PDN特性,其中周期性突发模式为最坏情况。PRBS模式可模拟实际IP开关活动的随机性。

以下广告时间

G
O
芯片SIPI设计课程视频培训
课程均可提供培训原视频


添加老师咨询

﹀
﹀
﹀

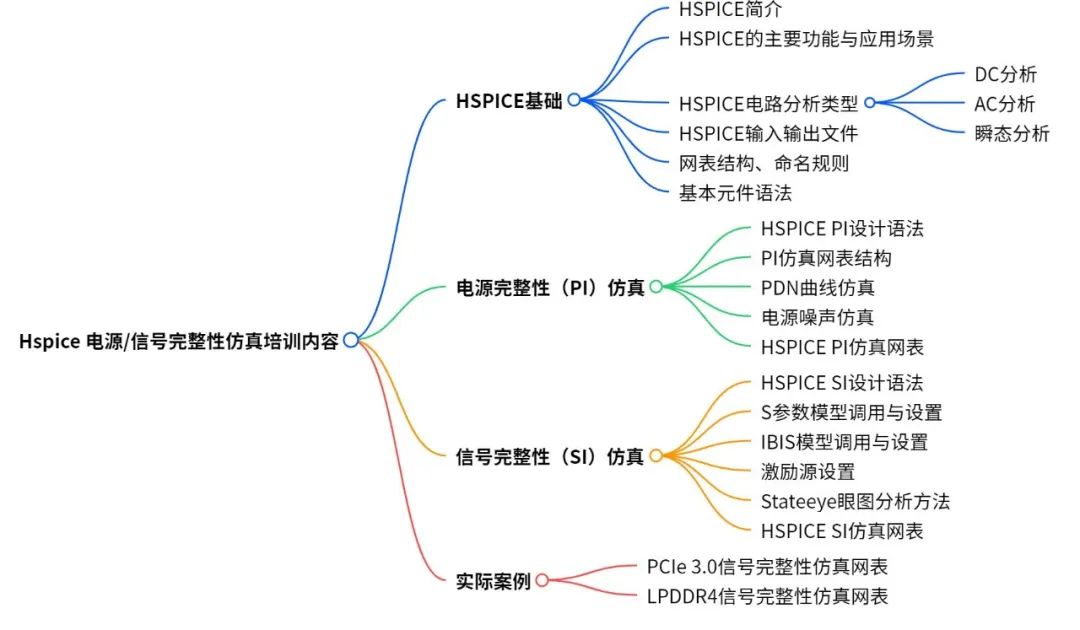
Hspice电源/信号完整性仿真培训

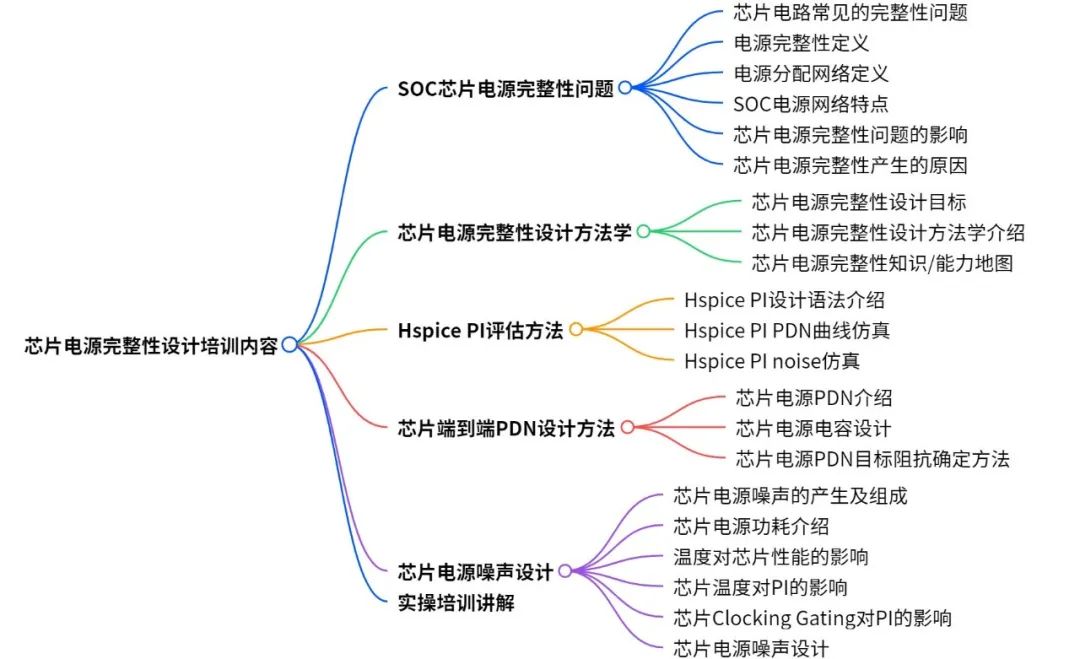
芯片电源完整性设计培训


LPDDR4 SIPI端到端设计培训


















