名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》
创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊)
专栏介绍:《Python星球日记》
目录
- 一、螺旋之美:当数学遇上艺术
- 二、环境准备:turtle库入门
- 1. 什么是Turtle图形库?
- 2. 基础设置技巧
- 三、核心实现:七种炫酷螺旋图案
- 1. 彩虹螺旋:最经典的入门图案
- 2. 斐波那契螺旋:自然界的黄金比例
- 3. 动态彩色螺旋:RGB数学魔法
- 四、数学原理深度解析
- 1. 螺旋的数学本质
- 2. 颜色空间的数学应用
- 五、交互功能:让艺术"活"起来
- 1. 模式切换系统
- 2. 用户体验优化
- 3. 绘制速度优化
- 4. 创意扩展方向
- 六、完整代码与总结
欢迎大家来到Python星球日记的趣学篇,在趣学篇,我们将带来很多有趣的适合初学者的项目,项目均由个人团队开发及AI vide coding的辅助…
用100多行Python代码就能创造出如梦如幻的螺旋图案,从彩虹般绚烂的色彩到斐波那契的自然美学,这就是编程艺术的魅力所在!今天我们来探索如何用Python的turtle库绘制各种令人惊叹的彩色螺旋图案。

一、螺旋之美:当数学遇上艺术
螺旋是自然界中最常见的几何形状之一,从海螺的外壳到银河系的旋臂,从向日葵的种子排列到人类的DNA双螺旋结构。当我们把这种自然之美搬到编程世界中,就能创造出令人叹为观止的数字艺术。
Python的turtle模块就像一支神奇的画笔,让我们能够轻松绘制各种复杂的图案。今天我们要实现的不仅仅是简单的螺旋,而是融合了数学美学、动态色彩和交互体验的综合作品。
二、环境准备:turtle库入门
1. 什么是Turtle图形库?
turtle(海龟绘图)是Python内置的图形库,灵感来源于Logo语言。想象一只小海龟在画布上爬行,它走过的路径就形成了图案。这种"过程性绘图"的方式特别适合理解和实现各种几何图形。
import turtle
import math# 创建画布和海龟对象
screen = turtle.Screen()
t = turtle.Turtle()

2. 基础设置技巧
在开始绘制复杂图案前,我们需要做一些优化设置:
def setup_screen():screen = turtle.Screen()screen.bgcolor("black") # 黑色背景更显炫酷screen.colormode(255) # 支持RGB颜色模式return screendef create_turtle():t = turtle.Turtle()t.speed(0) # 最快绘制速度t.pensize(2) # 适中的线条粗细return t
三、核心实现:七种炫酷螺旋图案
1. 彩虹螺旋:最经典的入门图案
彩虹螺旋是最容易理解也最具视觉冲击力的图案。它的核心思想是:随着螺旋的延伸,逐渐增加前进距离,同时循环使用彩虹色彩。
def rainbow_spiral(t, size=200):colors = ["red", "orange", "yellow", "green", "blue", "indigo", "violet"]for i in range(360):t.pencolor(colors[i % len(colors)]) # 循环使用颜色t.forward(i * size / 360) # 距离逐渐增加t.right(91) # 略大于90度的转角
关键技巧:
i * size / 360:让前进距离与循环次数成正比91度转角:比直角多1度,形成螺旋而非正方形- 颜色循环:
i % len(colors)确保颜色不断轮换
2. 斐波那契螺旋:自然界的黄金比例
斐波那契螺旋是大自然的杰作,从鹦鹉螺到向日葵都能看到它的身影。
def fibonacci_spiral(t, iterations=12):# 生成斐波那契数列fib = [1, 1]for i in range(iterations - 2):fib.append(fib[-1] + fib[-2])for size in fib:t.circle(size * 5, 90) # 画1/4圆弧t.left(90) # 转向下个方向
数学原理:每个1/4圆弧的半径都是斐波那契数列中的一个数,这样形成的螺旋符合黄金比例。
3. 动态彩色螺旋:RGB数学魔法
最有趣的部分是动态色彩生成。我们用数学函数来计算RGB值:
def colorful_square_spiral(t, size=300):for i in range(100):# 基于位置的RGB计算r = int(255 * (i / 100)) # 红色渐增g = int(255 * (1 - i / 100)) # 绿色渐减 b = int(128 + 127 * math.sin(i * 0.1)) # 蓝色正弦波动t.pencolor(r, g, b)t.forward(i * size / 100)t.right(89)

四、数学原理深度解析
1. 螺旋的数学本质
所有螺旋图案的核心都是极坐标方程。在我们的程序中,虽然使用的是turtle的直角坐标系统,但背后的数学原理是相通的:
阿基米德螺旋方程:r = a × θ
r:到原点的距离θ:角度a:螺旋的"紧密度"参数
def archimedes_spiral(t, turns=5, size=100):for i in range(turns * 360):angle = math.radians(i) # 角度转弧度radius = angle * size / (2 * math.pi) # 阿基米德公式# 极坐标转直角坐标x = radius * math.cos(angle)y = radius * math.sin(angle)t.goto(x, y)
2. 颜色空间的数学应用
我们使用三角函数来创建平滑的颜色过渡:
- 正弦函数:
sin(x)产生-1到1的周期性变化 - 映射到RGB:
128 + 127 * sin(x)将范围映射到0-255 - 相位差:不同颜色通道使用不同相位,产生丰富的色彩变化
# 创建彩虹效果的颜色计算
r = int(128 + 127 * math.sin(angle))
g = int(128 + 127 * math.sin(angle + math.pi/3)) # 相位差120度
b = int(128 + 127 * math.sin(angle + 2*math.pi/3)) # 相位差240度
五、交互功能:让艺术"活"起来
1. 模式切换系统
我们的程序实现了智能的图案切换系统,用户只需点击屏幕就能欣赏不同的螺旋艺术:
def main():patterns = [("彩虹螺旋", lambda: rainbow_spiral(t)),("斐波那契螺旋", lambda: fibonacci_spiral(t)),("星形螺旋", lambda: star_spiral(t)),# ... 更多图案]current_pattern = 0def next_pattern():nonlocal current_patternname, func = patterns[current_pattern]print(f"绘制: {name}")func()current_pattern = (current_pattern + 1) % len(patterns)screen.onscreenclick(lambda x, y: next_pattern())
2. 用户体验优化
- 即时反馈:点击后立即切换图案
- 循环播放:所有图案可以无限循环展示
- 控制台提示:显示当前绘制的图案名称## 六、性能优化与扩展建议
3. 绘制速度优化
# 关键优化技巧
t.speed(0) # 最快绘制速度
t.tracer(0) # 关闭动画,批量更新
# ... 绘制操作 ...
t.update() # 一次性显示结果
4. 创意扩展方向
- 音乐可视化:结合
pygame库,让螺旋随音乐节拍变化 - 参数化界面:添加滑块控制螺旋参数
- 3D效果:使用透视变换模拟立体螺旋
- 导出功能:保存高清图片或制作GIF动画
六、完整代码与总结
完整代码:
import turtle
import math
import randomdef setup_screen():"""设置画布"""screen = turtle.Screen()screen.bgcolor("black")screen.title("彩色螺旋数学图案")screen.setup(width=800, height=800)screen.colormode(255)return screendef create_turtle():"""创建海龟对象"""t = turtle.Turtle()t.speed(0) # 最快速度t.pensize(2)return tdef rainbow_spiral(t, size=200):"""彩虹螺旋图案"""t.clear()t.goto(0, 0)t.setheading(0)colors = ["red", "orange", "yellow", "green", "blue", "indigo", "violet"]for i in range(360):t.pencolor(colors[i % len(colors)])t.forward(i * size / 360)t.right(91)def fibonacci_spiral(t, iterations=12):"""斐波那契螺旋"""t.clear()t.goto(0, 0)t.setheading(0)t.pencolor("gold")# 斐波那契数列fib = [1, 1]for i in range(iterations - 2):fib.append(fib[-1] + fib[-2])for i, size in enumerate(fib):t.circle(size * 5, 90) # 画1/4圆弧t.left(90)def colorful_square_spiral(t, size=300):"""彩色方形螺旋"""t.clear()t.goto(0, 0)t.setheading(0)for i in range(100):# 生成渐变色r = int(255 * (i / 100))g = int(255 * (1 - i / 100))b = int(128 + 127 * math.sin(i * 0.1))t.pencolor(r, g, b)t.forward(i * size / 100)t.right(89)def flower_spiral(t, petals=8, size=150):"""花朵螺旋图案"""t.clear()t.goto(0, 0)t.setheading(0)for i in range(petals):# 每个花瓣使用不同颜色hue = i * 360 / petalsr = int(255 * (1 + math.cos(math.radians(hue))) / 2)g = int(255 * (1 + math.cos(math.radians(hue + 120))) / 2)b = int(255 * (1 + math.cos(math.radians(hue + 240))) / 2)t.pencolor(r, g, b)# 绘制花瓣for j in range(72):t.forward(size / 72)t.right(5)t.right(360 / petals)def archimedes_spiral(t, turns=5, size=100):"""阿基米德螺旋"""t.clear()t.goto(0, 0)t.setheading(0)for i in range(turns * 360):angle = math.radians(i)radius = angle * size / (2 * math.pi)# 彩色渐变r = int(128 + 127 * math.sin(angle))g = int(128 + 127 * math.sin(angle + math.pi/3))b = int(128 + 127 * math.sin(angle + 2*math.pi/3))t.pencolor(r, g, b)x = radius * math.cos(angle)y = radius * math.sin(angle)t.goto(x, y)def star_spiral(t, points=5, size=200):"""星形螺旋"""t.clear()t.goto(0, 0)t.setheading(0)for i in range(points * 72):# 动态调整颜色hue = (i * 5) % 360r = int(255 * (1 + math.sin(math.radians(hue))) / 2)g = int(255 * (1 + math.sin(math.radians(hue + 120))) / 2)b = int(255 * (1 + math.sin(math.radians(hue + 240))) / 2)t.pencolor(r, g, b)t.forward(i * size / (points * 72))t.right(360 / points + 1)def hypnotic_spiral(t, size=150):"""催眠螺旋图案"""t.clear()t.goto(0, 0)t.setheading(0)for i in range(500):# 创建催眠效果的颜色变化intensity = int(128 + 127 * math.sin(i * 0.1))t.pencolor(intensity, 0, 255 - intensity)t.forward(i * size / 500)t.right(91.1)def main():"""主函数 - 展示所有图案"""screen = setup_screen()t = create_turtle()patterns = [("彩虹螺旋", lambda: rainbow_spiral(t)),("斐波那契螺旋", lambda: fibonacci_spiral(t)),("彩色方形螺旋", lambda: colorful_square_spiral(t)),("花朵螺旋", lambda: flower_spiral(t)),("阿基米德螺旋", lambda: archimedes_spiral(t)),("星形螺旋", lambda: star_spiral(t)),("催眠螺旋", lambda: hypnotic_spiral(t))]current_pattern = 0def next_pattern():nonlocal current_patternname, func = patterns[current_pattern]print(f"绘制: {name}")func()current_pattern = (current_pattern + 1) % len(patterns)def on_click(x, y):next_pattern()# 绘制第一个图案next_pattern()# 设置点击事件screen.onscreenclick(on_click)print("点击屏幕切换图案,关闭窗口退出程序")screen.listen()screen.exitonclick()if __name__ == "__main__":main()
效果预览:
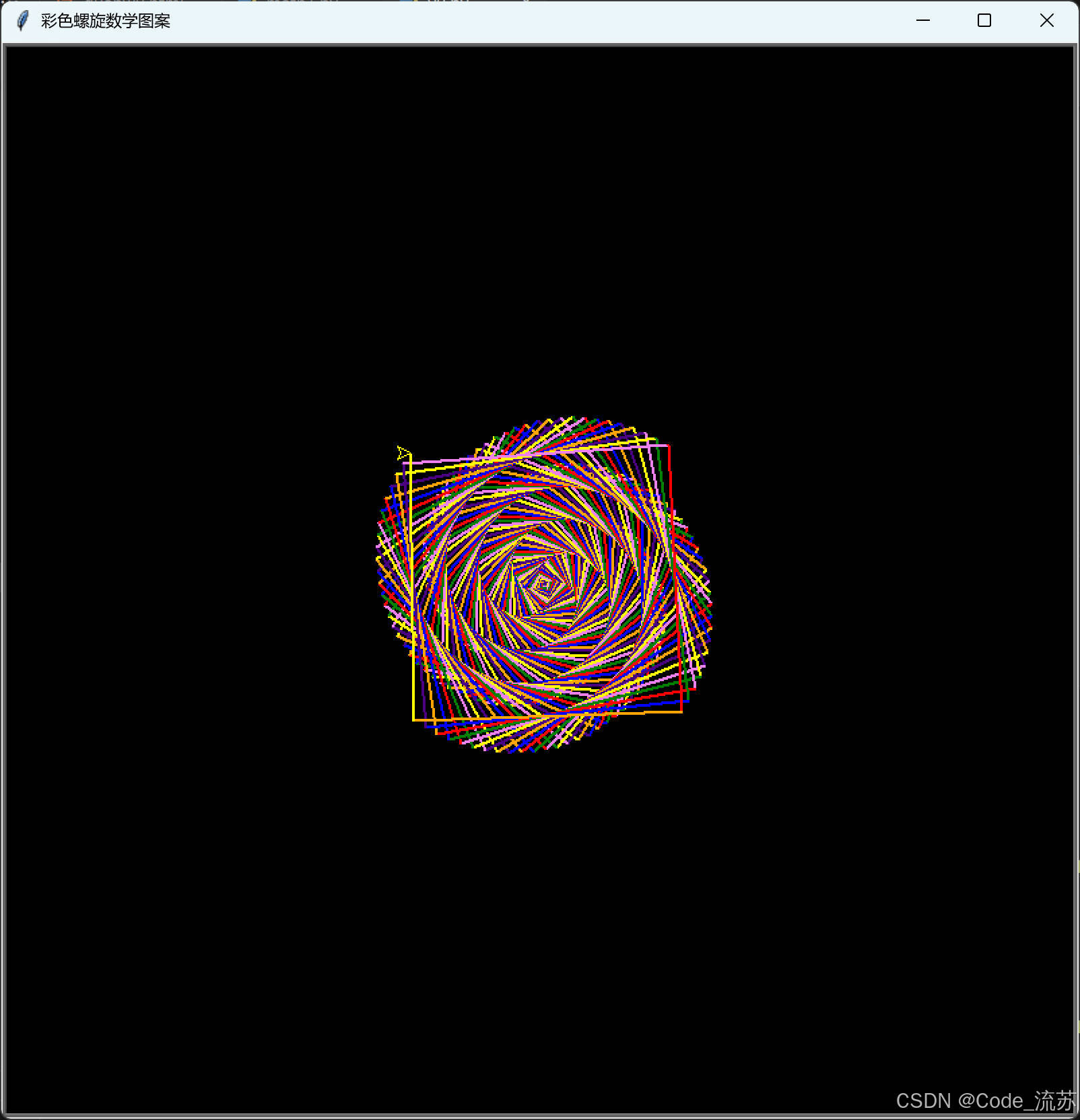
通过这个项目,我们不仅学会了用Python创造视觉艺术,更重要的是体验了数学之美在编程中的体现。从简单的turtle绘图到复杂的数学函数应用,从静态图案到动态交互,每一行代码都蕴含着数学与艺术的完美结合。
关键收获:
- 掌握了turtle库的高级应用技巧
- 理解了螺旋图案背后的数学原理
- 学会了用数学函数控制颜色变化
- 实现了用户友好的交互体验
编程不仅仅是逻辑和算法,它也是一种创造美的方式。当数学公式化作屏幕上跃动的彩色线条时,我们就在科技与艺术的交汇点上创造了属于数字时代的美学奇迹!
💡 小贴士:运行程序时,建议在全屏模式下欣赏,效果会更加震撼!记得点击屏幕体验不同的螺旋艺术哦~
创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊)








![[Java 基础]打印金字塔](https://i-blog.csdnimg.cn/img_convert/038d5b5699da962cbdb9127c227d33c9.png)







