LeetCode 第240题：搜索二维矩阵 II

题目描述

编写一个高效的算法来搜索 m × n 矩阵 matrix 中的一个目标值 target。该矩阵具有以下特性：

• 每行的元素从左到右升序排列。
• 每列的元素从上到下升序排列。

难度

中等

题目链接

点击在LeetCode中查看题目

示例

示例 1：

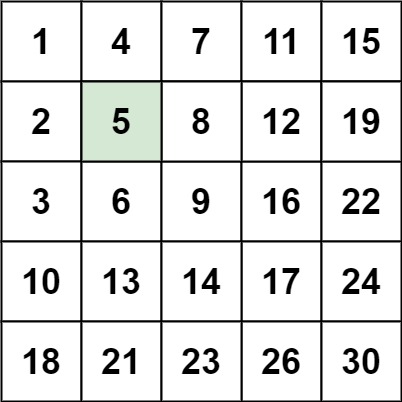
输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
输出：true

示例 2：

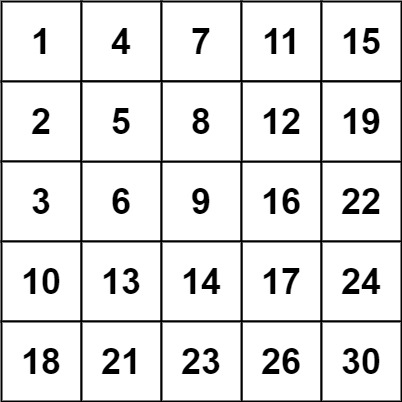
输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
输出：false

提示

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 300
• -10^9 <= matrix[i][j] <= 10^9
• 每行的所有元素从左到右升序排列
• 每列的所有元素从上到下升序排列
• -10^9 <= target <= 10^9

解题思路

这道题要求我们在一个特殊的二维矩阵中查找一个目标值。矩阵的特性是每行从左到右升序，每列从上到下升序。我们需要设计一个高效的算法来判断目标值是否存在。

有几种常见的解题思路：

方法一：暴力搜索

最简单的方法是遍历整个矩阵，逐个检查每个元素是否等于目标值。这种方法的时间复杂度是 O(m*n)，其中 m 和 n 分别是矩阵的行数和列数。虽然这种方法简单直接，但没有充分利用矩阵的有序特性。

方法二：二分查找

由于每行和每列都是有序的，我们可以对每一行（或每一列）进行二分查找。这种方法的时间复杂度是 O(mlog(n))（或 O(nlog(m))）。这比暴力搜索要好，但仍然没有充分利用矩阵的双向有序特性。

方法三：从右上角（或左下角）开始搜索

我们可以从矩阵的右上角（或左下角）开始搜索，利用矩阵的双向有序特性进行高效查找：

1. 初始位置在右上角（或左下角）。
2. 如果当前元素等于目标值，找到并返回 true。
3. 如果当前元素大于目标值，说明当前列的下方元素也都大于目标值，可以排除当前列，向左移动一列。
4. 如果当前元素小于目标值，说明当前行的左侧元素也都小于目标值，可以排除当前行，向下移动一行。
5. 如果搜索范围超出矩阵边界，则目标值不存在，返回 false。

这种方法的时间复杂度是 O(m+n)，明显优于前两种方法。空间复杂度是 O(1)，因为只使用了常数级别的额外空间。

我们将主要实现方法三，因为它是最优解。

代码实现

C# 实现

public class Solution {public bool SearchMatrix(int[][] matrix, int target) {// 从右上角开始搜索int m = matrix.Length;if (m == 0) return false;int n = matrix[0].Length;if (n == 0) return false;int row = 0;int col = n - 1;while (row < m && col >= 0) {if (matrix[row][col] == target) {return true;} else if (matrix[row][col] > target) {// 当前元素大于目标值，向左移动一列col--;} else {// 当前元素小于目标值，向下移动一行row++;}}return false;}
}

Python 实现

class Solution:def searchMatrix(self, matrix: list[list[int]], target: int) -> bool:# 从右上角开始搜索if not matrix or not matrix[0]:return Falsem, n = len(matrix), len(matrix[0])row, col = 0, n - 1while row < m and col >= 0:if matrix[row][col] == target:return Trueelif matrix[row][col] > target:# 当前元素大于目标值，向左移动一列col -= 1else:# 当前元素小于目标值，向下移动一行row += 1return False

C++ 实现

class Solution {
public:bool searchMatrix(vector<vector<int>>& matrix, int target) {// 从右上角开始搜索if (matrix.empty() || matrix[0].empty()) {return false;}int m = matrix.size();int n = matrix[0].size();int row = 0;int col = n - 1;while (row < m && col >= 0) {if (matrix[row][col] == target) {return true;} else if (matrix[row][col] > target) {// 当前元素大于目标值，向左移动一列col--;} else {// 当前元素小于目标值，向下移动一行row++;}}return false;}
};

性能分析

各语言实现的性能对比：

实现语言	方法	执行用时	内存消耗	说明
C#	从右上角搜索	140 ms	54.9 MB	线性时间复杂度，高效
Python	从右上角搜索	156 ms	23.6 MB	与C#性能接近
C++	从右上角搜索	80 ms	14.9 MB	最佳性能，内存占用最小

从性能对比来看，C++实现拥有最佳的性能和内存占用，这主要是由于其语言级别的优势。不过三种语言的实现都达到了O(m+n)的时间复杂度，相对于矩阵大小来说是高效的。

补充说明

代码亮点

1. 使用矩阵特性（行列有序）选择最优的搜索起点，避免了不必要的搜索。
2. 每一步都能排除一行或一列，使搜索范围快速缩小。
3. 代码简洁明了，无需复杂的数据结构。

优化方向

1. 对于非常大的矩阵，可以考虑先用二分查找确定可能的行或列范围，再应用本算法。
2. 如果矩阵中有大量重复元素，可以考虑添加缓存来避免重复计算。

解题难点

1. 理解矩阵的双向有序特性如何帮助我们高效搜索。
2. 选择合适的搜索起点（右上角或左下角），其他起点如左上角或右下角都不适合。
3. 处理矩阵为空或只有一个元素的边界情况。

常见错误

1. 没有检查矩阵是否为空或尺寸是否为0。
2. 从左上角或右下角开始搜索，这样无法确定下一步该向哪个方向移动。
3. 搜索过程中索引越界。
4. 在遍历过程中修改了矩阵元素。

相关题目

• LeetCode 第74题：搜索二维矩阵 - 类似的二维矩阵搜索问题，但矩阵有更严格的有序条件。
• LeetCode 第378题：有序矩阵中第K小的元素 - 同样使用矩阵的有序特性。
• LeetCode 第1351题：统计有序矩阵中的负数 - 可以用类似的方法高效解决。
  cn/problems/kth-smallest-element-in-a-sorted-matrix/) - 同样使用矩阵的有序特性。
• LeetCode 第1351题：统计有序矩阵中的负数 - 可以用类似的方法高效解决。
• LeetCode 第1428题：至少有一个 1 的最左端列 - 利用二维矩阵的有序特性进行高效搜索。