N皇后问题（回溯、启发式算法、随机算法）

article/2025/8/19 11:06:52

  • 题目描述
  • 回溯法
    • 所有解向量
    • 返回单个解
      • 伪代码
  • 启发式修补法
    • 原版
      • 伪代码
    • 改进版
      • 伪代码
  • 拉斯维加斯随机算法
    • 伪代码
    • 具体代码
  • 简单测试函数

题目描述

N皇后问题即为在一个n×n的棋盘上放置n个彼此不受攻击的皇后。按照国际象棋的规则，皇后可以攻击同行、同列或同一斜线上的棋子。等价于在n×n的棋盘放置n个皇后，使得任意两个皇后不在同一行、同一列以及同一斜线上。

Input:n(棋盘规格与皇后数量)
Output:n皇后问题的解向量

回溯法

N皇后问题的解空间可以用一棵完全n叉树表示，这意味着有nn种可能的解空间。
如果不进行剪枝那么时间复杂度会达到夸张的O(nn)。因此对于回溯法而言，难点在于确定适当的剪枝函数。
事实上我们能做到的就是控制其快速判断是否满足约定条件。

那么我们可以一行一行的放入皇后，这样就始终满足每一行只有一个皇后。这样我们的解空间规模就大致为n!。
那么该如何判断放入皇后的当前列和两条斜线有无皇后呢？
如果选择每次都循环判断的方式，那么每次插入都要经过时间复杂度为O(n)的判断，这显然是相当浪费时间的。
可以考虑用哈希的思想直接用一个bool数组记录每一列和每一对角线的是否放入皇后。下面以4皇后为例：
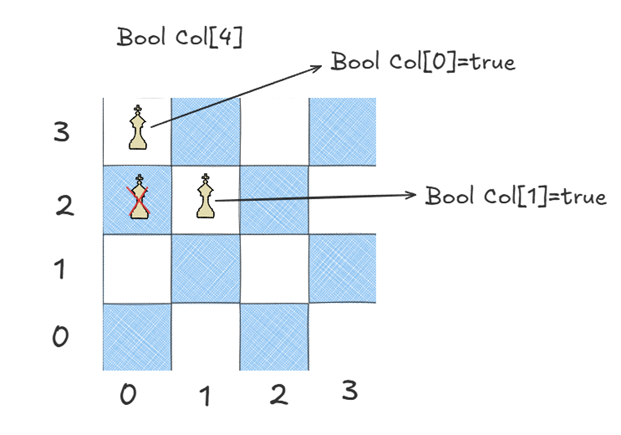
在这里插入图片描述
用Col记录列状态后，后续插入皇后只需用O(1)的时间复杂度即可判断该列有无皇后。但是对于对角线问题我们还没有解决，继而我们考虑一个n×n的棋盘有多少条副对角线，且满足什么状态：
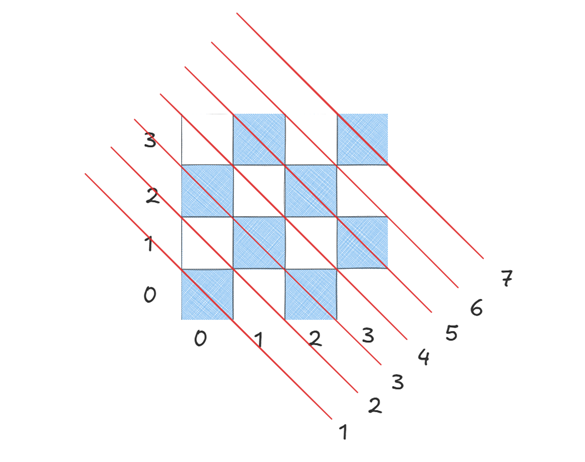
在这里插入图片描述
如上图我们不难发现，一个n×n的棋盘应当有2n-1条副对角线，且这些对角线都是同一斜率-1，这意味着他们都满足x+y=b，且b的取值范围为{0,1,2,3,4,5,6}.因此我们只需创建一个bool Dig2数组来记录每个皇后(x,y)对应的x+y是否为true，即可知道该皇后所在副对角线上有无其他皇后。

对于主对角线也是同理，不过需要注意的是主对角线上对角线满足的是x-y=b，且b的取值范围为{-3,-2,-1,0,1,2,3}因此boolDig1需要记录的是x-y+n-1位置的值。

有了上述三个数组我们就能做到O(1)的时间复杂度判断新插入的皇后是否满足约束条件。
这样我们从0行0列开始逐行插入，每一行都循环判断0到n列是否有能插入的位置，如果有就插入并判断下一行。如果没有则返回上一行，对上一行剩余位置继续查找符合约束条件的插入位置。如果顺利插入最后一行的皇后，则记录当前解空间并返回。

所有解向量

返回所有解:

void dfs(size_t row, vector<bool>& Col, vector<bool>& Dig1, vector<bool>& Dig2, vector<int>& Path, vector<vector<int>>& Ret)
{if (row == Path.size())//插入成功{Ret.push_back(Path);return;}for (int col = 0; col < Path.size(); col++)//尝试在这一行插入皇后{if (!Col[col] && !Dig1[row - col + Path.size() - 1] && !Dig2[row + col]){Path[row] = col;//插入当前位置Col[col] = Dig1[row - col + Path.size() - 1] = Dig2[row + col] = true;//记录已插入的列和对角线dfs(row + 1, Col, Dig1, Dig2, Path, Ret);//插入下一行Col[col] = Dig1[row - col + Path.size() - 1] = Dig2[row + col] = false;//恢复}}
}
vector<vector<int>> NQueens(size_t n)
{vector<bool>Col(n, false), Dig1(2 * n - 1, false), Dig2(2 * n - 1, false);vector<int>Path(n);vector<vector<int>>Ret;dfs(0, Col, Dig1, Dig2, Path, Ret);return Ret;
}

返回单个解

伪代码

function backtrackingNQueensOneSolution(n):Col = array of n false valuesDig1 = array of (2n-1) false valuesDig2 = array of (2n-1) false valuesPath = array of n integersif dfsOneSolution(0, Col, Dig1, Dig2, Path, n):return Pathelse:return empty arrayfunction dfsOneSolution(row, Col, Dig1, Dig2, Path, n):if row == n:return truefor col from 0 to n-1:diag1 = row - col + n - 1diag2 = row + colif not Col[col] and not Dig1[diag1] and not Dig2[diag2]:Path[row] = colCol[col] = trueDig1[diag1] = trueDig2[diag2] = trueif dfsOneSolution(row+1, Col, Dig1, Dig2, Path, n):return trueCol[col] = falseDig1[diag1] = falseDig2[diag2] = falsereturn false
bool dfsOneSolution(size_t row, vector<bool>& Col, vector<bool>& Dig1, vector<bool>& Dig2, vector<int>& Path) {if (row == Path.size()) {return true; // 找到解}for (int col = 0; col < Path.size(); col++) {if (!Col[col] && !Dig1[row - col + Path.size() - 1] && !Dig2[row + col]) {Path[row] = col;Col[col] = Dig1[row - col + Path.size() - 1] = Dig2[row + col] = true;//记录已经插入过的列、对角线// 递归搜索下一行，如果找到解则立即返回if (dfsOneSolution(row + 1, Col, Dig1, Dig2, Path)) {return true;}// 回溯Col[col] = Dig1[row - col + Path.size() - 1] = Dig2[row + col] = false;}}return false; // 当前行所有列都尝试过，无解
}vector<int> backtrackingNQueensOneSolution(size_t n) 
{vector<bool> Col(n, false);vector<bool> Dig1(2 * n - 1, false);vector<bool> Dig2(2 * n - 1, false);vector<int> Path(n);if (dfsOneSolution(0, Col, Dig1, Dig2, Path)) {return Path; // 返回找到的解}return {}; // 未找到解（实际上n>3时总有解）
}

启发式修补法

我们可以先随机将皇后放入棋盘中，并确保行和列不冲突。并且统计每个位置的冲突数，然后将每行的皇后移动至冲突数最小的位置，然后重新统计冲突数，如果冲突数为0，则返回，否则继续。如下图所示：
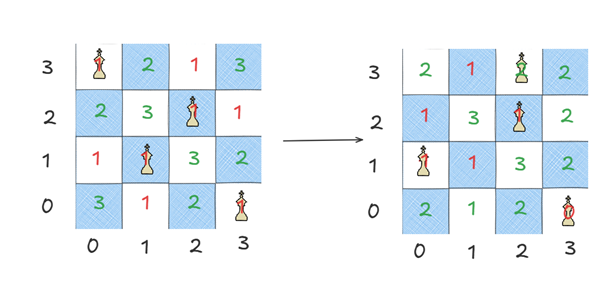
在这里插入图片描述
可以发现冲突最小值的位置有时候不止一个，那么我们随机选择其中一个即可。然而在具体实现中，我发现将所有皇后移动至冲突最小的位置，不仅效率低下，关键是很容易造成死循环。因此不得不记录下已经走过的状态，因而导致效率进一步下降。

所以对其进行简单的改进，就是每次只需移动冲突最大的皇后即可。比如上图的状态可以移动至如下：
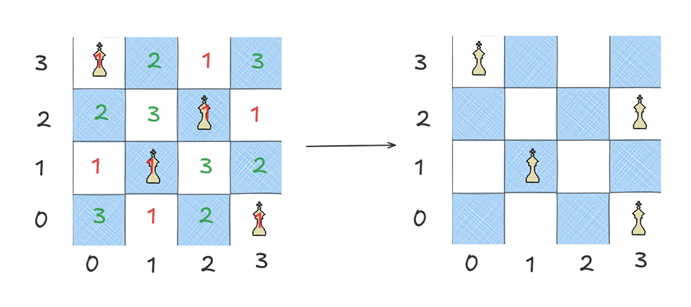
在这里插入图片描述

不难发现，冲突最大位置的皇后有时候也不仅一个，我们同样是随机选择其中一个移动。这样强大的随机性就极大地避免了死循环的可能。

原版

伪代码

function heuristicRepairNQueens(n, maxIter):Col = zeros(n)      # 列冲突计数Dig1 = zeros(2n-1)  # 主对角线冲突计数Dig2 = zeros(2n-1)  # 副对角线冲突计数Path = array of n integersRandomArrange(Path, Col, Dig1, Dig2)  # 随机初始化Mins = array of n integers (init to n+1)Conflicts = n x n matrixConflictsRows = list of n listsseen = empty setfor iter from maxIter downto 0:if IsComplete(Path, Col, Dig1, Dig2):return PathCountConflicts(Path, Col, Dig1, Dig2, Mins, Conflicts, ConflictsRows)# 移动所有皇后for row from 0 to n-1:oldcol = Path[row]newcol = random choice from ConflictsRows[row]# 更新冲突计数Dig1[row - oldcol + n - 1] -= 1Dig2[row + oldcol] -= 1Col[oldcol] -= 1Dig1[row - newcol + n - 1] += 1Dig2[row + newcol] += 1Col[newcol] += 1Path[row] = newcol# 处理循环while Path in seen and iter > 0:RandomArrange(Path, Col, Dig1, Dig2)iter -= 1add Path to seenreturn empty array  # 未找到解

移动所以皇后：

void RandomArrange(vector<int>& Path, vector<int>& Col, vector<int>& Dig1, vector<int>& Dig2)
{random_device rd;mt19937 gen(rd());int n = Path.size();//初始化列、对角线的皇后fill(Col.begin(), Col.end(), 0);fill(Dig1.begin(), Dig1.end(), 0);fill(Dig2.begin(), Dig2.end(), 0);for (size_t row = 0; row < n; row++){size_t col = gen() % n;//确保列不冲突while (Col[col])col = gen() % n;Path[row] = col;Col[col] = 1;//记录对角线上皇后个数++Dig1[row - col + n - 1];++Dig2[row + col];}
}bool IsComplete(vector<int>& Path, vector<int>& Col, vector<int>& Dig1, vector<int>& Dig2)
{int n = Path.size();for (size_t row = 0; row < n; row++){int col = Path[row];if (Col[col] + Dig1[row - col + n - 1] + Dig2[row + col] != 3){return false;}}return true;
}void CountConflicts(vector<int>& Path, vector<int>& Col, vector<int>& Dig1, vector<int>& Dig2, vector<int>&Mins, vector<vector<int>>& Conflicts, vector<vector<int>>& ConflictsRows)
{int n = Path.size();for (size_t row = 0; row < n; row++){//初始化最小值Mins[row] = n + 1;for (size_t col = 0; col < n; col++){Conflicts[row][col] = Dig1[row - col + n - 1] + Dig2[row + col] + Col[col];if (Path[row] == col)Conflicts[row][col] -= 3;Mins[row] = min(Mins[row], Conflicts[row][col]);}}for (size_t row = 0; row < n; row++){//初始化最小值位置ConflictsRows[row].clear();for (size_t col = 0; col < n; col++){if (Conflicts[row][col] == Mins[row])ConflictsRows[row].push_back(col);}}
}vector<int> heuristicRepairNQueens(size_t n, int maxIter = 10000) 
{// 随机初始化：每行、每列一个皇后，列位置随机vector<int> Col(n);//记录各个主副对角线上皇后个数vector<int> Dig1(2 * n - 1);vector<int> Dig2(2 * n - 1);vector<int> Path(n);random_device rd;mt19937 gen(rd());//随机生成棋盘RandomArrange(Path, Col, Dig1, Dig2);//记录每行冲突最小的值vector<int>Mins(n,n+1);// 冲突统计冲突个数vector<vector<int>>Conflicts(n, vector<int>(n));//记录每行冲突最小的位置vector<vector<int>>ConflictsRows(n);//记录当前路径是否已经存在set<vector<int>>st;for (int i = maxIter; i >= 0; i--){//判断是否插入完成，如果插入完成则返回if (IsComplete(Path, Col, Dig1, Dig2))return Path;//没有插入完成则更新冲突数组CountConflicts(Path, Col, Dig1, Dig2, Mins, Conflicts, ConflictsRows);////PrintQueen(Path);//cout << endl;//将皇后移动至冲突最小位置//有可能导致列冲突for (size_t row = 0; row < n; row++){int oldcol = Path[row];int newcol = ConflictsRows[row][gen() % (ConflictsRows[row].size())];//移动皇后Path[row] = newcol;//记录新的对角线皇后个数--Dig1[row - oldcol + n - 1];--Dig2[row + oldcol];++Dig1[row - newcol + n - 1];++Dig2[row + newcol];//记录新的列皇后个数--Col[oldcol];++Col[newcol];}//如果当前路径已经被记录，则重新随机生成棋盘while(!st.insert(Path).second&&i){RandomArrange(Path, Col, Dig1, Dig2);i--;}}return {}; // 未找到解
}

改进版

伪代码

function greedyRepairNQueens(n, maxIter):Path, Col, Dig1, Dig2 = random initial arrangementfor iter from 0 to maxIter-1:if IsComplete(Path, Col, Dig1, Dig2):return Path# 找最大冲突皇后maxConflicts = -1conflictRows = empty listfor row from 0 to n-1:col = Path[row]conflicts = Col[col] + Dig1[row-col+n-1] + Dig2[row+col] - 3if conflicts > maxConflicts:maxConflicts = conflictsconflictRows = [row]else if conflicts == maxConflicts:add row to conflictRowsrow = random choice from conflictRowsoldcol = Path[row]minConflicts = ∞bestCol = oldcol# 找最小冲突位置for col from 0 to n-1:if col == oldcol: continueconflicts = Col[col] + Dig1[row-col+n-1] + Dig2[row+col]if conflicts < minConflicts:minConflicts = conflictsbestCol = colif bestCol ≠ oldcol:# 移动皇后update conflict countselse:RandomArrange(Path, Col, Dig1, Dig2)return empty array
vector<int> greedyRepairNQueens(int n, int maxIter = 10000) 
{vector<int> Path(n), Col(n), Dig1(2 * n - 1), Dig2(2 * n - 1);RandomArrange(Path, Col, Dig1, Dig2);random_device rd;mt19937 gen(rd());for (int iter = 0; iter < maxIter; iter++) {if (IsComplete(Path, Col, Dig1, Dig2)) return Path;//记录已插入皇后位置的最大冲突数int maxConflicts = 0;vector<int> conflictRows;for (int row = 0; row < n; row++) {int col = Path[row];int conflicts = Col[col] + Dig1[row - col + n - 1] + Dig2[row + col] - 3;if (conflicts > maxConflicts) {maxConflicts = conflicts;conflictRows.clear();conflictRows.push_back(row);}else if (conflicts == maxConflicts) {conflictRows.push_back(row);}}//随机选择一个最大冲突的皇后int row = conflictRows[gen() % conflictRows.size()];int oldcol = Path[row];int bestCol = oldcol;//记录当前行最小冲突位置int minConflicts = n + 1;for (int col = 0; col < n; col++) {if (col == oldcol) continue;int conflicts = Col[col] + Dig1[row - col + n - 1] + Dig2[row + col];if (conflicts < minConflicts) {minConflicts = conflicts;bestCol = col;}}if (bestCol != oldcol) {Path[row] = bestCol;--Col[oldcol];--Dig1[row - oldcol + n - 1];--Dig2[row + oldcol];++Col[bestCol];++Dig1[row - bestCol + n - 1];++Dig2[row + bestCol];}else//为移动则重排{RandomArrange(Path, Col, Dig1, Dig2);}}return {}; // 未找到解
}

拉斯维加斯随机算法

我们可以先随机放入前k个然后再进行回溯。具体思路参考回溯这里就不多做赘述。

伪代码

function lasVegasHybridNQueens(n, k, maxTries):for attempt from 0 to maxTries-1:Col = array of n false valuesDig1 = array of (2n-1) false valuesDig2 = array of (2n-1) false valuesPath = array of n integersif randomPlaceFirstK(k, n, Path, Col, Dig1, Dig2):if backtrack(k, n, Path, Col, Dig1, Dig2):return Pathreturn empty arrayfunction randomPlaceFirstK(k, n, Path, Col, Dig1, Dig2):for row from 0 to k-1:candidates = []for col from 0 to n-1:diag1 = row - col + n - 1diag2 = row + colif not Col[col] and not Dig1[diag1] and not Dig2[diag2]:add col to candidatesif candidates is empty:return falsecol = random choice from candidatesPath[row] = colCol[col] = trueDig1[diag1] = trueDig2[diag2] = truereturn truefunction backtrack(row, n, Path, Col, Dig1, Dig2):# 标准回溯算法（从指定行开始）# 同前文回溯算法实现

具体代码

// 回溯法，从第 row 行开始补全剩余皇后
bool backtrack(int row, int n, vector<int>& Path, vector<bool>& Col, vector<bool>& Dig1, vector<bool>& Dig2) 
{if (row == n) return true;for (int col = 0; col < n; ++col) {if (!Col[col] && !Dig1[row - col + n - 1] && !Dig2[row + col]){Path[row] = col;//记录插入位置列、对角线Col[col] = Dig1[row - col + n - 1] = Dig2[row + col] = true;//插入完成if (backtrack(row + 1, n, Path, Col, Dig1, Dig2)) return true;//回溯Col[col] = Dig1[row - col + n - 1] = Dig2[row + col] = false;}}return false;
}// 前 K 行随机放置皇后，若成功返回 true，否则 false
bool randomPlaceFirstK(int k, int n, vector<int>& Path, mt19937& gen, vector<bool>&Col, vector<bool>&Dig1, vector<bool>&Dig2)
{for (int row = 0; row < k; ++row) {vector<int> candidates;for (int col = 0; col < n; ++col) {if (!Col[col]&& !Dig1[row-col+n-1]&& !Dig2[row+col]) {candidates.push_back(col);}}//插入失败if (candidates.empty()) return false;//插入成功int col = candidates[gen() % candidates.size()];Path[row] = col;Col[col] = Dig1[row - col + n - 1] = Dig2[row + col] = true;}return true;
}// 主函数：拉斯维加斯 + 回溯法
vector<int> lasVegasHybridNQueens(int n, int k = 5, int maxTries = 10000) 
{random_device rd;mt19937 gen(rd());vector<int> Path(n);vector<bool>Col(n, false), Dig1(2 * n - 1, false), Dig2(2 * n - 1, false);for (int attempt = 0; attempt < maxTries; attempt++){if (randomPlaceFirstK(k, n, Path, gen,Col,Dig1,Dig2)) {if (backtrack(k, n, Path, Col, Dig1, Dig2)){return Path;}}}return {}; // 未找到解
}

简单测试函数

int main()
{cout << "回溯法" << endl;size_t begin = clock();backtrackingNQueensOneSolution(20);size_t end = clock();cout << "规模:" << 20 << " 时间：" << end - begin << "ms" << endl;begin = clock();backtrackingNQueensOneSolution(30);end = clock();cout << "规模:" << 30 << " 时间：" << end - begin << "ms" << endl;begin = clock();backtrackingNQueensOneSolution(33);end = clock();cout << "规模:" << 33 << " 时间：" << end - begin << "ms" << endl;cout << "启发式修补法原版" << endl;size_t begin1 = clock();heuristicRepairNQueens(500);size_t end1 = clock();cout << "规模:" << 500 << " 时间：" << end1 - begin1 << "ms" << endl;begin1 = clock();heuristicRepairNQueens(550);end1 = clock();cout << "规模:" << 550 << " 时间：" << end1 - begin1 << "ms" << endl;cout << "启发式修补法改进版" << endl;size_t begin2 = clock();greedyRepairNQueens(200000);size_t end2 = clock();cout << "规模:" << 200000 << " 时间：" << end2 - begin2 << "ms" << endl;begin2 = clock();greedyRepairNQueens(300000);end2 = clock();cout << "规模:" << 300000 << " 时间：" << end2 - begin2 << "ms" << endl;cout << "拉斯维加斯随机算法" << endl;size_t begin3 = clock();lasVegasHybridNQueens(36);size_t end3 = clock();cout << "规模:" << 36 << " 时间：" << end3 - begin3 << "ms" << endl;}

运行结果：
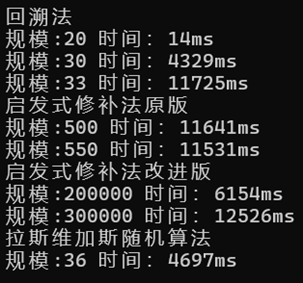
在这里插入图片描述
从中可以看出回溯法的效率式最差的，拉斯维加斯随机算法则次之，适合中规模。启发式修补法效率则远高于上述两者，适合大规模求解。


http://www.hkcw.cn/article/lHDmkWQpwk.shtml

相关文章

华为OD机试真题——战场索敌（2025A卷：100分）Java/python/JavaScript/C/C++/GO最佳实现

华为OD机试真题——战场索敌（2025A卷：100分）Java/python/JavaScript/C/C++/GO最佳实现

2025 A卷 100分 题型 本专栏内全部题目均提供Java、python、JavaScript、C、C++、GO六种语言的最佳实现方式； 并且每种语言均涵盖详细的问题分析、解题思路、代码实现、代码详解、3个测试用例以及综合分析； 本文收录于专栏：《2025华为OD真题目录+全流程解析+备考攻略+经验分…
阅读更多...
企业文件乱、传输慢？用群晖 NAS 构建安全高效的共享系统

企业文件乱、传输慢？用群晖 NAS 构建安全高效的共享系统

在信息化办公不断加速的今天&#xff0c;企业对文件存储、共享与安全管理的需求愈发严苛。传统文件共享方式效率低下、权限混乱、远程访问困难&#xff0c;极大影响了协同办公效率。此时&#xff0c;一套可靠、高效、安全的文件共享解决方案便成为众多企业的“刚需”。 这正是…
阅读更多...
IDEA项目推送到远程仓库

IDEA项目推送到远程仓库

打开IDEA——>VCS——>Creat Git 选择项目 push提交到本地 创建远程仓库 复制地址 定义远程仓库 推送 推送成功
阅读更多...
被院士当年的毕业论文惊艳到 深耕科技育英才

被院士当年的毕业论文惊艳到 深耕科技育英才

被院士当年的毕业论文惊艳到 深耕科技育英才！在南京大学，有一群杰出的学者致力于国家重大需求和世界科技前沿的研究。他们不仅在科研道路上不断探索，还培养了大量青年科学家。在中国科学院学部成立70周年及第九个“全国科技工作者日”之际，中国科学院推出了“遇见先生”系列…
阅读更多...
加拿大多地野火肆虐进入紧急状态 武装部队驰援

加拿大多地野火肆虐进入紧急状态 武装部队驰援

加拿大多地野火肆虐进入紧急状态 武装部队驰援！近日，加拿大多地遭受野火侵袭。中部马尼托巴省于28日宣布进入紧急状态，政府将派遣武装部队前往救援。5月25日，在加拿大艾伯塔省斯旺希尔斯附近，野火燃烧引发滚滚浓烟。同月27日，麦克默里堡附近的野火也产生了大量浓烟。此外…
阅读更多...
GESP2024年6月认证C++二级( 第三部分编程题（2）计数）

GESP2024年6月认证C++二级( 第三部分编程题（2）计数）

参考程序&#xff1a; #include <iostream> using namespace std;// 函数 check(x, y)&#xff1a;统计一个整数 x 中有多少位是数字 y int check(int x, int y) {int cnt 0; // 统计 y 出现的次数while (x > 0) { // 逐位处理 x 中的每一位int tmp x % …
阅读更多...
手动移植FreeRTOS

手动移植FreeRTOS

好记性不如烂笔头&#xff0c;之前也移植时一直忘记记录一下&#xff0c;这次刚好项目用上就步步记录一下防止下次忘记&#xff0c;同时也希望对同行有所帮助&#xff0c;不求别的只为一个点赞和关注&#xff0c;就能给我带来极大的虚荣心和情绪价值&#xff0c;谢谢。 第一步…
阅读更多...
决策分析工具篇

决策分析工具篇

为了便于决策分析绘图&#xff0c;开发了影响图和决策树的绘图工具&#xff0c;用于学习和演练。 1.支持不同类型的节点&#xff0c;对于不确定性节点的概率和要求为1. 2.支持连接线。 3.支持导出绘图为图片 4.不存储用户数据&#xff0c;即时使用。 影响图提供了一种紧凑且直…
阅读更多...
国际乒联选举现场乱成一锅粥 投票争议引发混乱

国际乒联选举现场乱成一锅粥 投票争议引发混乱

国际乒联选举现场乱成一锅粥。当地时间5月27日，2025年国际乒联代表大会在卡塔尔多哈召开期间，因主席选举争议导致会议临时暂停。投票过程中，现任主席佩特拉索林以104票的微弱优势连任，而卡塔尔候选人艾哈迈德哈利勒阿尔穆罕纳获得102票落选。卡塔尔一方对选举过程表示不满，…
阅读更多...
胖东来红内裤案宣判，被告段某赔偿40万 名誉权纠纷落锤

胖东来红内裤案宣判，被告段某赔偿40万 名誉权纠纷落锤

2025年5月28日，许昌市魏都区人民法院公开审理了许昌市胖东来商贸集团有限公司与段某之间的名誉权纠纷案，并当庭宣判。法院判决段某在其个人抖音账号“两个小段（小）”发布经法院审核的书面道歉信视频，且该视频在发布后30日内不得删除；同时，段某需赔偿许昌市胖东来商贸集团…
阅读更多...
俞敏洪骑车摔倒深夜发文回应 报平安继续前行

俞敏洪骑车摔倒深夜发文回应 报平安继续前行

俞敏洪骑车摔倒深夜发文回应！5月29日，新东方创始人、东方甄选董事长兼CEO俞敏洪在青海骑行时摔倒，膝盖等处磕破出血。他正在挑战360公里环青海湖骑行，在海拔3200米以上骑行100公里，爬坡700米以上。30日凌晨1点多，俞敏洪发微博报平安：“29日骑车有点睡着了摔了一下，感谢…
阅读更多...
博主向胖东来道歉视频30天不能删 名誉权案判决结果

博主向胖东来道歉视频30天不能删 名誉权案判决结果

2025年5月28日，河南许昌市魏都区人民法院公开审理了原告许昌市胖东来商贸集团有限公司与被告段某的名誉权纠纷案，并当庭宣判。法院判决段某在其个人抖音账号“两个小段（小）”上发布书面道歉信视频，内容需经法院审核，且发布后30日内不得删除；段某还需赔偿许昌市胖东来商贸…
阅读更多...
web ui自动化工具playwright

web ui自动化工具playwright

playwright是微软开源的一款web ui自动化工具&#xff0c;该工具有很多亮点&#xff0c;解决以前困扰web UI自动化测试的很多难点。这篇博客将介绍playwright主要特点。 playwright支持录制减少了编写成本 如果要使用playwright的录制功能&#xff0c;有两种途径&#xff0c;途…
阅读更多...
刘若英执导新剧被指抄袭 剧情结构引争议

刘若英执导新剧被指抄袭 剧情结构引争议

近日，刘若英自编自导的新剧《忘了我记得》被指抄袭美剧《了不起的麦瑟尔夫人》。有人指出两部剧的情节和结构非常相似，甚至人物设定也存在重叠。批评者认为，《忘了我记得》不仅在整体框架上模仿了《了不起的麦瑟尔夫人》，而且喜剧段子和单口部分也没有达到预期效果。特别是…
阅读更多...
陈伟跨市调任廊坊三河市委书记 新职务开启新篇章

陈伟跨市调任廊坊三河市委书记 新职务开启新篇章

陈伟近日已从河北保定蠡县县委书记调任廊坊三河市委书记。公开资料显示，陈伟1975年11月出生，河北安国人，1996年11月参加工作，1997年7月加入中国共产党，拥有省委党校研究生学历。陈伟长期在保定市工作，历任多个职务，包括安国市纪检委常务副书记、监察局长，博野县委常委、…
阅读更多...
6月起这些新规影响你我生活 多项政策助力民生与发展

6月起这些新规影响你我生活 多项政策助力民生与发展

6月起这些新规影响你我生活 多项政策助力民生与发展！《中华人民共和国学前教育法》自2025年6月1日起施行。该法强调发展学前教育需坚持政府主导，以政府举办为主，大力发展普惠性学前教育。国家将建立学前教育资助制度，有条件的地方逐步推进实施免费学前教育。幼儿园要科学实…
阅读更多...
广东海南疑似火流星划过 夜空巨响引关注

广东海南疑似火流星划过 夜空巨响引关注

广东海南疑似火流星划过 夜空巨响引关注！5月28日晚，广东网友发布视频称，“突然一声巨响，天都被照亮了。”随后，茂名巨响和火流星的话题在网络上引发关注。据中国气象爱好者消息，一颗火流星划破粤西的夜空。有评论区网友表示，这次火流星规模较大，不仅广东西部，海南北部…
阅读更多...
day13 leetcode-hot100-24（链表3）

day13 leetcode-hot100-24（链表3）

234. 回文链表 - 力扣&#xff08;LeetCode&#xff09; 1.转化法 思路 将链表转化为列表进行比较 复习到的知识 arraylist的长度函数&#xff1a;list.size() 具体代码 /*** Definition for singly-linked list.* public class ListNode {* int val;* ListNode ne…
阅读更多...
vue+threeJs 生成云状特效屏幕

vue+threeJs 生成云状特效屏幕

嗨&#xff0c;我是小路。今天主要和大家分享的主题是“vuethreeJs 生成云状特效屏幕”。 动态云状特效示例图 二、实例代码 <!--创建一个动态数字屏幕--> <template><div class"pageBox"><div class"leftBox" ref"lef…
阅读更多...
【穷举】数字方格

【穷举】数字方格

题目描述 如上图&#xff0c;有3个方格&#xff0c;每个方格里面都有一个整数a1&#xff0c;a2&#xff0c;a3。&#xff08;0 < a1, a2, a3 < n&#xff09; 而且a1 a2是2的倍数&#xff0c;a2 a3是3的倍数&#xff0c; a1 a2 a3是5的倍数。 你的任务是找到一组a1…
阅读更多...
推荐文章

Copyright @ 2022~2023