同步教材
同步教案
第一单元四则运算教材分析
(一)教材说明:这一单元是这册书中一个重点单元。本单元主要教学并梳理混合运算的顺序。混合运算前面学生已经学会按从左往右的顺序计算两步式题,并且知道括号的作用,这里主要教学含有两级运算的运算顺序,并对所学的混合运算的顺序进行整理。其主要内容有:整理同级运算的顺序,教学并整理含两级运算的顺序及含有小括号的运算顺序、有关0的运算。
(二)教学目标:
1、进一步掌握含有两级运算的运算顺序,正确计算三步式题。
2、经历探索和交流解决实际问题的过程中,感受解决问题的一些策略和方法,学会用两、三步计算的方法解决一些实际问题。
3、在解决实际问题的过程中,养成认真审题、独立思考等学习习惯。
(三)、学情分析:
学生已经学习掌握了加.减.乘.除四种运算的计算方法,有了进行混合运算的基础;
计算课的教学,学生相对会感到枯燥乏味,教学时应创设具体生活情境,在情境中解决实际问题,在解决问题中理解运算顺序,提高学生学习的兴趣
由于学生的逻辑思维不够强,理解表达能力有限,教学中应该注意依托情境问题,培养学生的理解能力。
(四)教学重点:熟练掌握四则混合运算顺序加带有括号的混合运算顺序。
(五)教学难点:四则混合运算顺序的学习。
(六)教学建议:
本单元中一个新的亮点就是整理混合运算的顺序是结合解决问题进行的。目标中学生既要掌握运算顺序,又要理解解决问题的基本策略和步骤。从学生的角度看,学生已经有了一定的运算基础,因此建议:
知识与技能:以应用题型为经,以运算顺序为纬。视学生情况,各有侧重。
过程与方法:加强基础运算,保证计算的正确率。
在本单元的教学中,我们应该尝试给学生提供探索的机会,让学生经历创造的过程,从中体会运算顺序的合理性和小括号的意义。
情感态度价值观:在探索过程中,学生的思维是自主的,学生的选择是开放的,学生的表述也是多样的。
(七)、教法与学法:本单元教学内容是在学生学习掌握了加.减.乘.除四种运算的基础上,进一步探究学习混合运算的运算顺序和方法.教学中,首先创设生活情境,提高学生的学习兴趣,激发学生的求知欲望;再采用演绎推理法,使学生在情景中解决实际问题,在解决问题中理解同时掌握四则混合运算的计算,并通过小组合作,总结归纳四则混合运算的运算顺序,掌握知识形成技能;然后通过形式多样的练习,加强训练.提高计算能力和解决问题的能力,发展学生的思维,发展学生的智力。
(八)教学时间安排:9节
加减法的意义和各部分间的关系 第1节
教学内容:例1 “做一做”
教材学情分析:
学生已经学习掌握了加.减.乘.除四种运算的计算方法,有了进行混合运算的基础;计算课的教学,学生相对会感到枯燥乏味,教学时应创设具体生活情境,在情境中解决实际问题,在解决问题中理解运算顺序,提高学生学习的兴趣;由于学生的逻辑思维不够强,理解表达能力有限,教学中应该注意依托情境问题,培养学生的理解能力。
教学目标:
知识与技能:从实例中归纳加减法的意义和关系,初步理解加法与减法的意义以及它们之间互逆关系。
过程与方法:初步学会利用加减法算式中各部分之间的关系求解加减法算式中的未知数。
情感态度价值观:培养学生发现数学知识和运用数学知识解决问题的能力。
教学重点:理解加、减法的意义和利用加减法的关系求加减法中的未知量。
教学难点:从实例中探究加、减法的互逆关系。
教法与学法:首先创设生活情境,提高学生的学习兴趣,激发学生的求知欲望;再采用演绎推理法,使学生在情景中解决实际问题,在解决问题中理解同时掌握四则混合运算的计算,并通过小组合作,总结归纳四则混合运算的运算顺序,掌握知识形成技能;然后通过形式多样的练习,加强训练.提高计算能力和解决问题的能力,发展学生的思维,发展学生的智力。
教学准备:多媒体课件
教学过程
一、复习导入
1、口算
2、笔算
3、导入
二、理解加减法的意义
1、理解加法的意义。
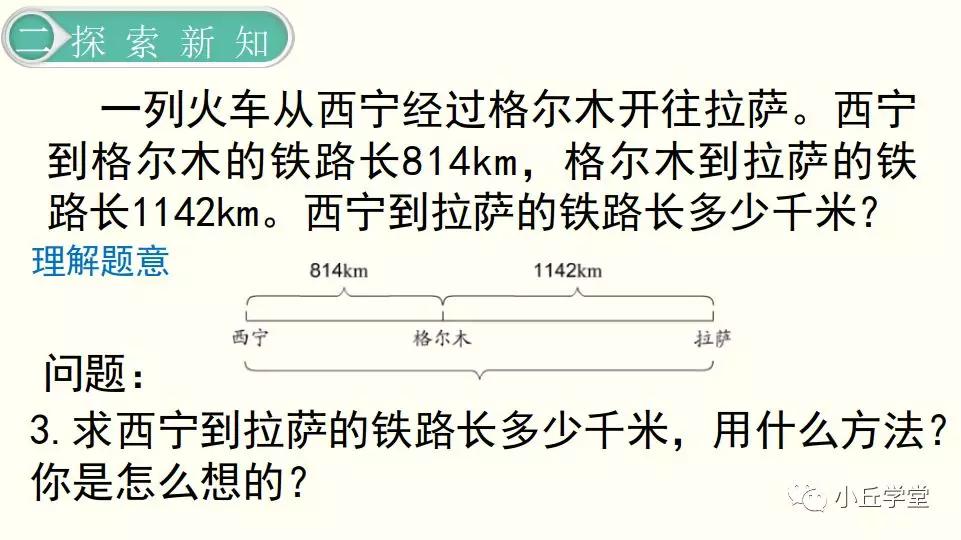
出示例1(1) 一列火车从西宁经过格尔木开往拉萨。西宁到格尔木的铁路长814 km,格尔木到拉萨的铁路长1142 km。西宁到拉萨的铁路长多少千米?
(1)问:根据这道题你收集到了哪些信息?
(让学生尝试用线段图表示)
(2)请学生根据线段图写出加法算式。
814+1142=1956 或 1142+814=1956
师:为什么用加法呢?那怎样的运算叫做加法?(小组讨论)
(根据这两个算式,结合已有的知识讨论并试着用语言表示什么是加法。)
(3)小结:把两个数合并成一个数的运算,叫做加法。(出示加法的意义)说明加法各部分名称
2、理解减法的意义
能不能试着把这道加法应用题改编成减法应用题呢?
(1)根据学生的回答,出示例1(2)(3)尝试用线段图表示:
师:根据线段图写出两道减法算式,并说说这样列式的理由。
1956-814=1142 或 1956-1142=814
(2)问:怎样的运算是减法?(小组讨论)
(根据这两个算式,结合已有的知识讨论并试着用语言表示)
(3)小结:已知两个加数的和与其中的一个加数,求另一个加数的运算,叫做减法。(出示)
(4)说明减法各部分名称
三、探究、理解加法和减法之间的关系。
1.问:上面的这些算式,你觉得它们之间有什么联系?观察上述四道算式中数字位置间关系,思考加法和减法之间的关系。然后以小组的形式进行讨论。(小组讨论。个别汇报)
2.根据学生的汇报,出示:
加数 + 加数 = 和 被减数 - 减数 = 差
3.师归纳并小结:减法是加法的逆运算。(板书)
4.加法各部分之间的关系。
出示:814+1142=1956
814=1956-1142
1142=1956-814
问:观察算式,你能得到什么结论?
和=加数+加数
加数=和-另一个加数
5.减法各部分之间的关系。
出示:800-350=450
800=450+350
350=800-450
问:通过观察这组算式,你能得出减法各部分的关系吗?
观察这组算式讨论归纳得出:
被减数=差+减数 减数=被减数-差
6.练习“做一做”
四、总结
师:谁来说说我们这节课学习了些什么?你知道了什么呢?
板书设计:加减法的意义和各部分间的关系
814+1142=1956 加数+加数=和
1956-1142=814 和-一个加数=另一个加数
1956-814=1142
课件演示






同步练习
第1课时 加、减法的意义和各部分间的关系
1.填空题。
(1)一个加数是45,另一个加数与它相同,它们的和是( )。
(2)在一个减法算式中,差是150,减数是64,被减数是( )。
(3)减法是( )的逆运算。
(4)两个加数的和是579,其中一个加数是278,另一个加数是( )。
(5)被减数是354,差是79,减数是( )。
2.根据给出的算式填空。
(1)476-168=308 308+( )=476 476-( )=168
(2)256+128=384 384-( )=128 384-( )=256
3.小马虎在做一道减法题时,把减数72错写成27,这时得到的差是309。正确的差是多少?
答案提示
1. (1) 90 (2) 214 (3) 加法 (4)301 (5) 275
2. (1) 168 308 (2) 256 128
3.解法一:
309+27=336 336-72=264
答:正确的差是264。
解法二:
72-27=45 309-45=264
答:正确的差是264。