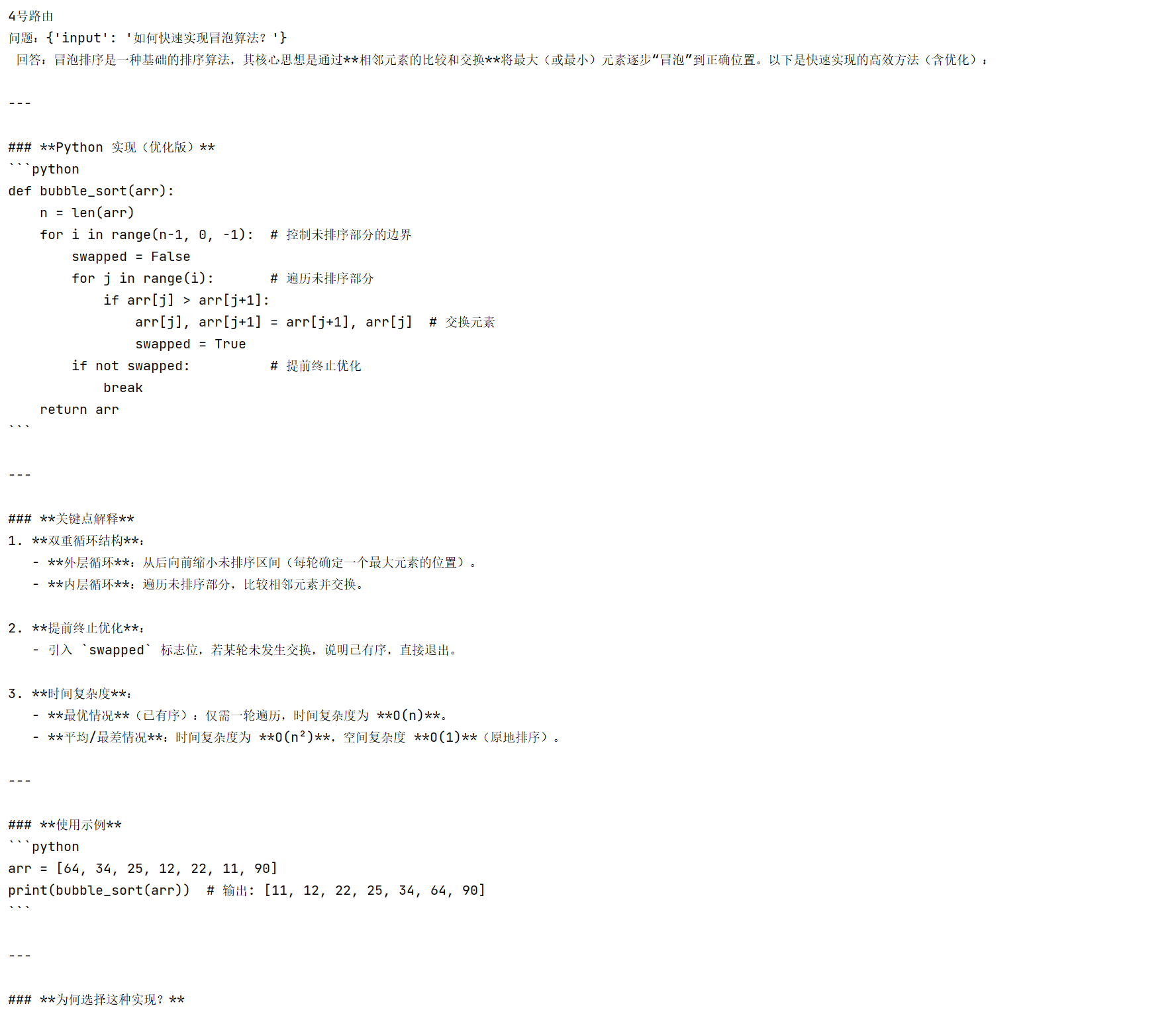
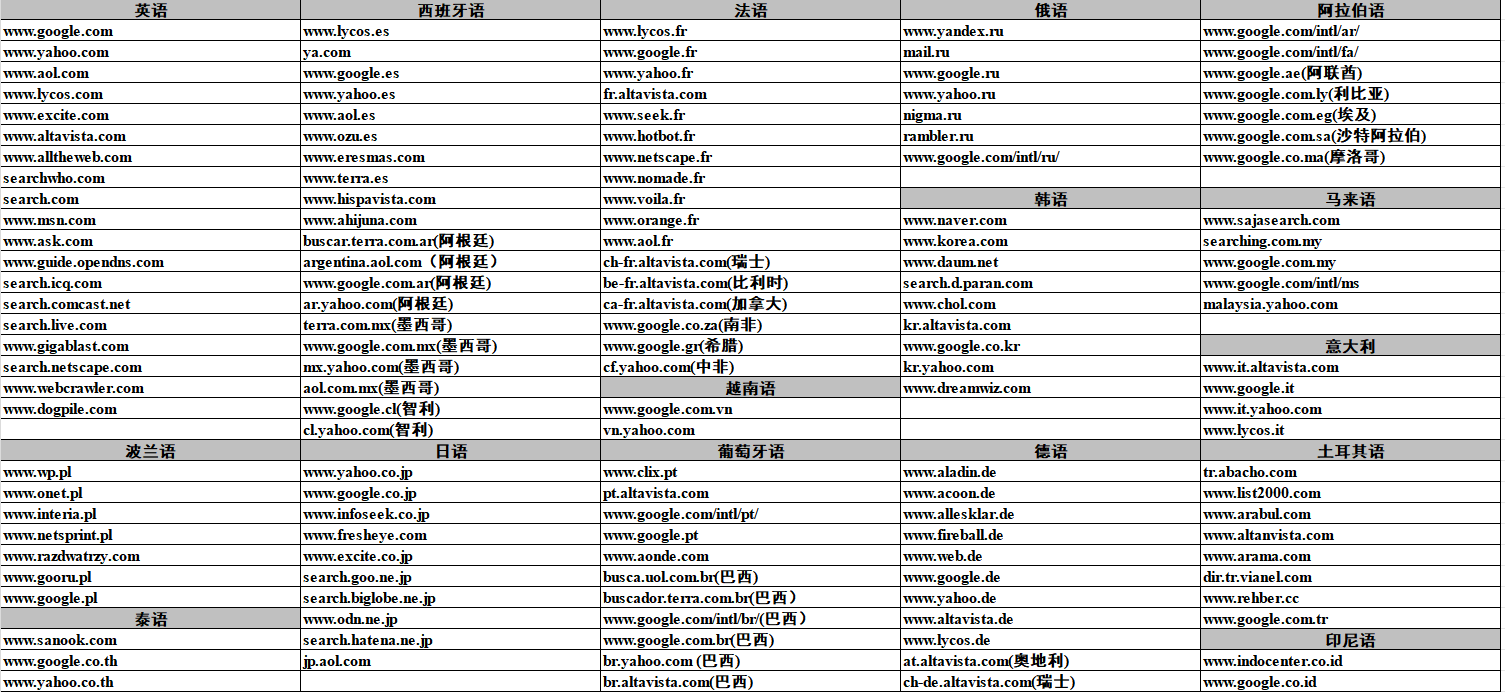
在三维空间中，一个 $3\times 1$ 向量可以转换为一个 $3\times 3$ 的反对称矩阵。这种转换在物理学、机器人学和计算机视觉等领域非常有用。本文将详细介绍如何在 Python 的 SymPy 库中定义和使用这种反对称矩阵。

数学背景

对于一个三维向量 $\mathbf{v}=\left[\begin{array}{c}{v}_1\\ v_2\\ v_3\end{array}\right]$，其对应的反对称矩阵定义为：

$$[\mathbf{v}{]}_{\times }=\left[\begin{array}{ccc}0& -v_3& v_2\\ v_3& 0& -v_1\\ -v_2& v_1& 0\end{array}\right]$$

这个矩阵满足反对称性质$$[\mathbf{v}{]}_{\times }^T=-[\mathbf{v}{]}_{\times }$$
它的一个重要应用是向量叉积的矩阵形式：$$\mathbf{v}\times \mathbf{w}=[\mathbf{v}{]}_{\times }\mathbf{w}$$

在 SymPy 中实现

定义符号向量和反对称矩阵

首先，我们需要导入 SymPy 并定义符号变量：

from sympy import symbols, Matrix# 定义符号变量
v1, v2, v3 = symbols('v1 v2 v3')# 创建3×1的符号向量
v = Matrix([v1, v2, v3])# 定义反对称矩阵的函数
def create_skew_symmetric_matrix(vector):return Matrix([[0,      -vector[2], vector[1]],[vector[2], 0,      -vector[0]],[-vector[1], vector[0], 0]])# 获取符号向量对应的反对称矩阵
skew_v = create_skew_symmetric_matrix(v)print("符号向量：")
print(v)print("\n对应的反对称矩阵：")
print(skew_v)

向量叉积的矩阵形式

利用反对称矩阵，我们可以方便地计算向量叉积：

# 定义另一个符号向量
w1, w2, w3 = symbols('w1 w2 w3')
w = Matrix([w1, w2, w3])# 计算向量叉积的矩阵形式
cross_product = skew_v * wprint("\n向量叉积的矩阵形式：")
print(cross_product)# 验证是否等于直接计算向量叉积
from sympy import simplify
fork = simplify(v.cross(w) - cross_product)
print("\n验证是否等于向量叉积（结果应为零矩阵）：")
print(fork)

使用数值向量

我们也可以使用具体的数值向量来验证：

# 数值向量
v_num = Matrix([1, 2, 3])# 创建对应的反对称矩阵
skew_v_num = create_skew_symmetric_matrix(v_num)print("\n数值向量：")
print(v_num)print("\n对应的反对称矩阵：")
print(skew_v_num)# 数值叉积验证
w_num = Matrix([4, 5, 6])
cross_product_num = skew_v_num * w_num
print("\n数值叉积：")
print(cross_product_num)# 直接计算向量叉积对比
print("\n直接计算向量叉积：")
print(v_num.cross(w_num))

验证反对称性质

最后，我们可以验证反对称矩阵的性质：

print("\n验证反对称矩阵的转置是否等于其负矩阵：")
print(simplify(skew_v_num.transpose() + skew_v_num))

总结

通过 SymPy，我们可以方便地定义和操作三维向量的反对称矩阵。这种矩阵在几何变换和物理模拟中有广泛的应用。本文提供的代码示例展示了如何从符号到数值计算整个过程，帮助理解和应用这一数学工具。