目录
聚类结果分析与簇类型推断学习笔记
一、聚类后分析基础流程
1.1 基本分析步骤
1.2 常用可视化工具
二、簇特征分析方法
2.1 数值型特征分析
簇中心对比
雷达图展示
2.2 类别型特征分析
频数统计
卡方检验
三、簇类型推断技术
3.1 基于统计特征的推断
关键指标计算
特征重要性排序
3.2 基于业务规则的标签分配
业务规则示例(电商场景)
3.3 自动化标签生成(NLP技术)
使用TF-IDF生成标签
四、验证与优化方法
4.1 簇稳定性检验
重采样验证
4.2 业务合理性验证
专家评估表设计
五、实战案例:客户分群分析
5.1 RFM模型聚类
5.2 簇类型定义
六、常见问题解决方案
6.1 簇难以解释的情况
6.2 混合型数据处理
作业:接续 day17 内容
5簇的含义
4簇的含义
3簇类型推断
2推断簇的类型
1 推断簇的类型
0推断簇的类型
聚类结果分析与簇类型推断学习笔记
一、聚类后分析基础流程
1.1 基本分析步骤
-
可视化检查:降维后观察簇分布
-
统计特征:计算各簇的统计量
-
对比分析:识别簇间差异特征
-
业务解释:结合领域知识赋予语义
1.2 常用可视化工具
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA# 降维可视化
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X)plt.scatter(X_pca[:,0], X_pca[:,1], c=labels, cmap='viridis')
plt.title("Cluster Visualization (PCA)")
plt.show()二、簇特征分析方法
2.1 数值型特征分析
簇中心对比
import pandas as pd# 计算各簇中心
centers = pd.DataFrame(scaler.inverse_transform(kmeans.cluster_centers_),columns=feature_names
)# 可视化
centers.plot(kind='bar', figsize=(12,6))
plt.title("Cluster Centers Comparison")
plt.ylabel("Feature Value (Original Scale)")
plt.xticks(rotation=0)
plt.show()雷达图展示
from math import pi# 准备数据
categories = centers.columns
N = len(categories)
angles = [n / float(N) * 2 * pi for n in range(N)]
angles += angles[:1]fig = plt.figure(figsize=(8,8))
ax = fig.add_subplot(111, polar=True)for i in range(len(centers)):values = centers.iloc[i].values.flatten().tolist()values += values[:1]ax.plot(angles, values, linewidth=1, label=f'Cluster {i}')ax.fill(angles, values, alpha=0.1)ax.set_xticks(angles[:-1])
ax.set_xticklabels(categories)
plt.legend(loc='upper right')
plt.title("Cluster Profiles (Radar Chart)")
plt.show()2.2 类别型特征分析
频数统计
# 添加聚类标签到原始数据
data['cluster'] = labels# 分类变量分析
for col in categorical_cols:cross_tab = pd.crosstab(data['cluster'], data[col], normalize='index')cross_tab.plot(kind='bar', stacked=True, figsize=(10,4))plt.title(f"Distribution of {col} by Cluster")plt.ylabel("Proportion")plt.show()卡方检验
from scipy.stats import chi2_contingencyfor col in categorical_cols:contingency_table = pd.crosstab(data['cluster'], data[col])chi2, p, _, _ = chi2_contingency(contingency_table)print(f"{col}: χ²={chi2:.1f}, p={p:.3f}")三、簇类型推断技术
3.1 基于统计特征的推断
关键指标计算
cluster_stats = data.groupby('cluster').agg({'age': ['mean', 'std'],'income': ['median', 'min', 'max'],'purchase_frequency': 'mean'
})# 标准化比较
normalized_stats = cluster_stats.apply(lambda x: (x - x.mean()) / x.std(), axis=0
)特征重要性排序
# 计算簇间差异最大的特征
feature_importance = {}
for col in numeric_cols:f_val, p_val = f_oneway(*[data[data['cluster']==i][col] for i in range(n_clusters)])feature_importance[col] = f_valsorted_features = sorted(feature_importance.items(), key=lambda x: -x[1])3.2 基于业务规则的标签分配
业务规则示例(电商场景)
def assign_cluster_label(row):if row['recency'] > 30 and row['frequency'] < 2:return '流失风险客户'elif row['monetary'] > 500 and row['frequency'] > 5:return '高价值客户'else:return '普通客户'data['cluster_label'] = data.apply(assign_cluster_label, axis=1)3.3 自动化标签生成(NLP技术)
使用TF-IDF生成标签
from sklearn.feature_extraction.text import TfidfVectorizer# 假设有文本型特征
tfidf = TfidfVectorizer(max_features=50)
tfidf_matrix = tfidf.fit_transform(data['text_feature'])# 聚合每个簇的关键词
for i in range(n_clusters):cluster_tfidf = tfidf_matrix[labels==i].mean(axis=0)top_words_idx = cluster_tfidf.argsort()[0,-3:][::-1]top_words = [tfidf.get_feature_names_out()[i] for i in top_words_idx]print(f"Cluster {i} 关键词:", ", ".join(top_words))四、验证与优化方法
4.1 簇稳定性检验
重采样验证
from sklearn.utils import resamplestability_scores = []
for _ in range(10):# 重采样X_sample = resample(X, random_state=42)# 重新聚类kmeans_sample = KMeans(n_clusters=3).fit(X_sample)# 计算相似度(使用调整兰德指数)ari = adjusted_rand_score(labels, kmeans_sample.labels_)stability_scores.append(ari)print(f"平均稳定性得分: {np.mean(stability_scores):.3f}")4.2 业务合理性验证
专家评估表设计
| 簇ID | 主要特征 | 假设类型 | 业务合理性(1-5) | 备注 |
|---|---|---|---|---|
| 0 | 高收入低频 | 潜在VIP | 4 | 需激活消费频率 |
| 1 | 低收入高频 | 价格敏感 | 5 | 适合促销活动 |
五、实战案例:客户分群分析
5.1 RFM模型聚类
# 计算RFM指标
recency = (current_date - purchase_dates).dt.days
frequency = purchase_history.groupby('customer_id').size()
monetary = purchase_history.groupby('customer_id')['amount'].sum()# 标准化
rfm = pd.DataFrame({'Recency': recency, 'Frequency': frequency, 'Monetary': monetary})
rfm_scaled = StandardScaler().fit_transform(rfm)# 聚类
kmeans = KMeans(n_clusters=5)
rfm['cluster'] = kmeans.fit_predict(rfm_scaled)5.2 簇类型定义
| 簇 | Recency | Frequency | Monetary | 类型标签 | 营销策略 |
|---|---|---|---|---|---|
| 0 | 低(新近) | 高 | 高 | 冠军客户 | 专属服务/高端推荐 |
| 1 | 高(久远) | 低 | 低 | 流失客户 | 唤醒优惠/问卷调查 |
| 2 | 中 | 中 | 中 | 潜力客户 | 交叉销售/忠诚计划 |
六、常见问题解决方案
6.1 簇难以解释的情况
解决方案:
-
尝试不同聚类算法(如DBSCAN可能发现密度簇)
-
增加/减少簇数量
-
使用特征选择技术去除噪声特征
-
尝试不同的特征组合或衍生新特征
6.2 混合型数据处理
处理流程:
from sklearn.compose import ColumnTransformer
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import OneHotEncoder# 数值型和类别型分别处理
preprocessor = ColumnTransformer(transformers=[('num', StandardScaler(), numeric_cols),('cat', OneHotEncoder(), categorical_cols)])# 构建聚类流水线
cluster_pipe = Pipeline([('preprocess', preprocessor),('cluster', KMeans(n_clusters=3))
])作业:接续 day17 内容
接续 DAY17 的内容, 对 kmeans 聚类后的簇类型进行分析:
x1= X.drop('KMeans_Cluster',axis=1) # 删除聚类标签列
y1 = X['KMeans_Cluster']
# 构建随机森林,用shap重要性来筛选重要性
import shap
import numpy as np
from sklearn.ensemble import RandomForestClassifier # 随机森林分类器
model = RandomForestClassifier(n_estimators=100, random_state=42) # 随机森林模型
model.fit(x1, y1) # 训练模型,此时无需在意准确率 直接全部数据用来训练了
shap.initjs()# 初始化 SHAP 解释器
explainer = shap.TreeExplainer(model)
shap_values = explainer.shap_values(x1) # 这个计算耗时
shap_values.shape # 第一维是样本数,第二维是特征数,第三维是类别数SHAP 特征重要性条形图,挑选出最重要的四个特征进行分析
# --- 1. SHAP 特征重要性条形图 (Summary Plot - Bar) ---
print("--- 1. SHAP 特征重要性条形图 ---")
shap.summary_plot(shap_values[:, :, 0], x1, plot_type="bar",show=False) # 这里的show=False表示不直接显示图形,这样可以继续用plt来修改元素,不然就直接输出了
plt.title("SHAP Feature Importance (Bar Plot)")
plt.show()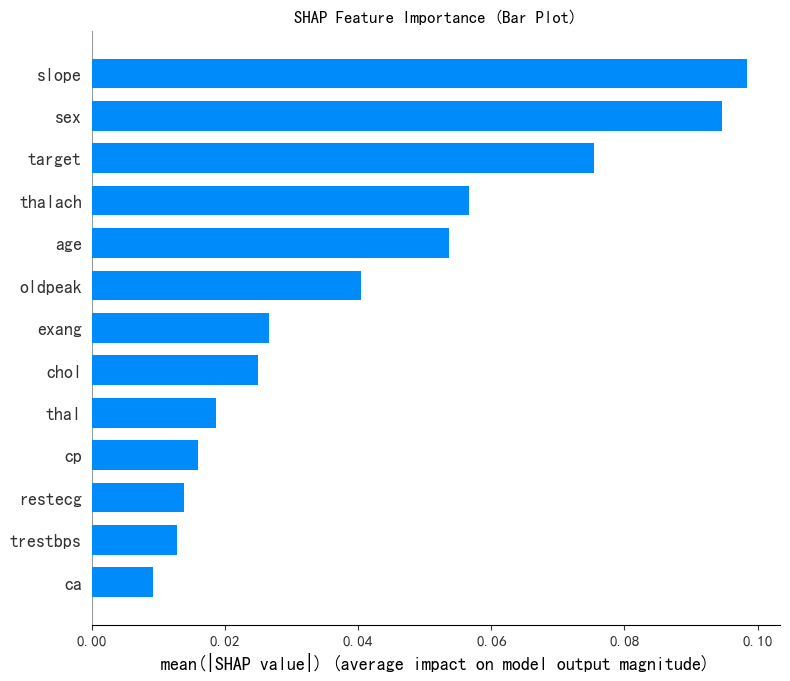
判断一下这几个特征是离散型还是连续型:
# 此时判断一下这几个特征是离散型还是连续型
import pandas as pd
selected_features = [ 'slope','sex', 'target', 'thalach']for feature in selected_features:unique_count = X[feature].nunique() # 唯一值指的是在某一列或某个特征中,不重复出现的值# 连续型变量通常有很多唯一值,而离散型变量的唯一值较少print(f'{feature} 的唯一值数量: {unique_count}')if unique_count < 10: # 这里 10 是一个经验阈值,可以根据实际情况调整print(f'{feature} 可能是离散型变量')else:print(f'{feature} 可能是连续型变量')
总样本中的前四个重要性的特征分布图
# X["Purpose_debt consolidation"].value_counts() # 统计每个唯一值的出现次数
import matplotlib.pyplot as plt# 总样本中的前四个重要性的特征分布图
fig, axes = plt.subplots(2, 2, figsize=(12, 8))
axes = axes.flatten()for i, feature in enumerate(selected_features):axes[i].hist(X[feature], bins=20)axes[i].set_title(f'Histogram of {feature}')axes[i].set_xlabel(feature)axes[i].set_ylabel('Frequency')plt.tight_layout()
plt.show()
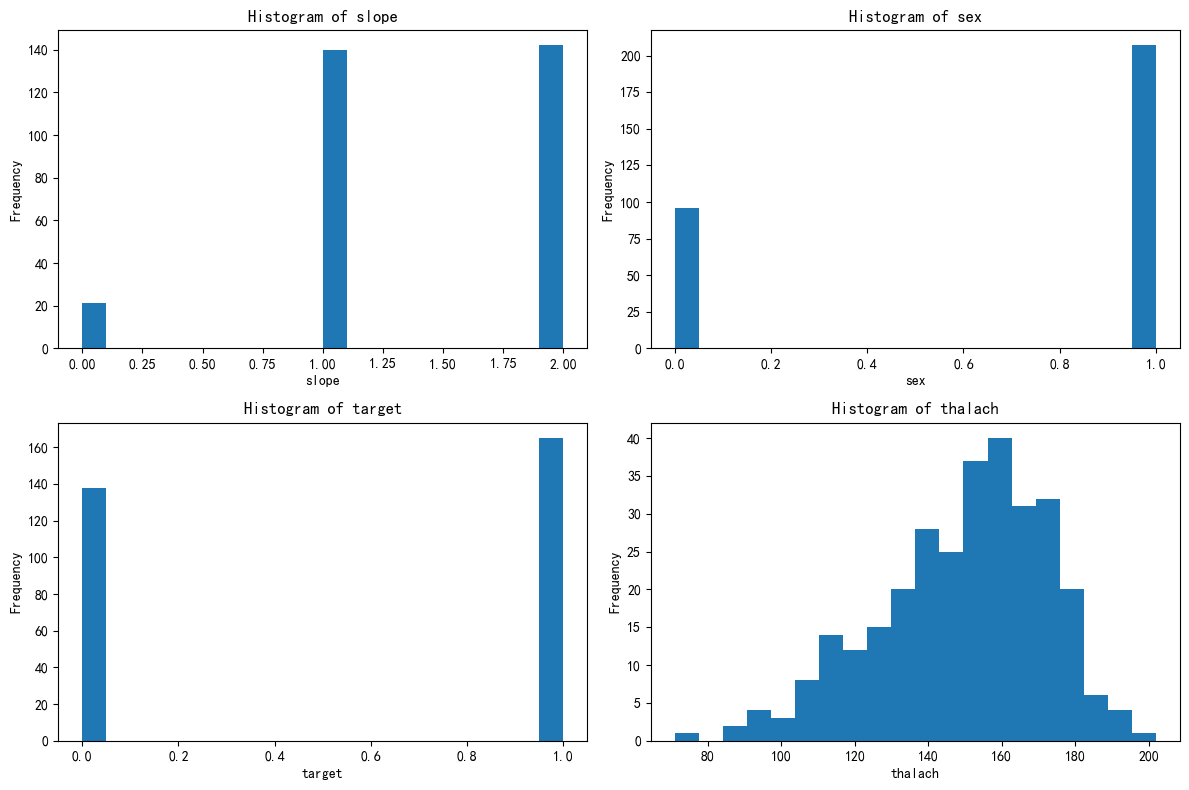
# 绘制出每个簇对应的这四个特征的分布图
X[['KMeans_Cluster']].value_counts()查看簇数

# 分别筛选出每个簇的数据
X_cluster0 = X[X['KMeans_Cluster'] == 0]
X_cluster1 = X[X['KMeans_Cluster'] == 1]
X_cluster2 = X[X['KMeans_Cluster'] == 2]
X_cluster3 = X[X['KMeans_Cluster'] == 3]
X_cluster4 = X[X['KMeans_Cluster'] == 4]
X_cluster5 = X[X['KMeans_Cluster'] == 5]
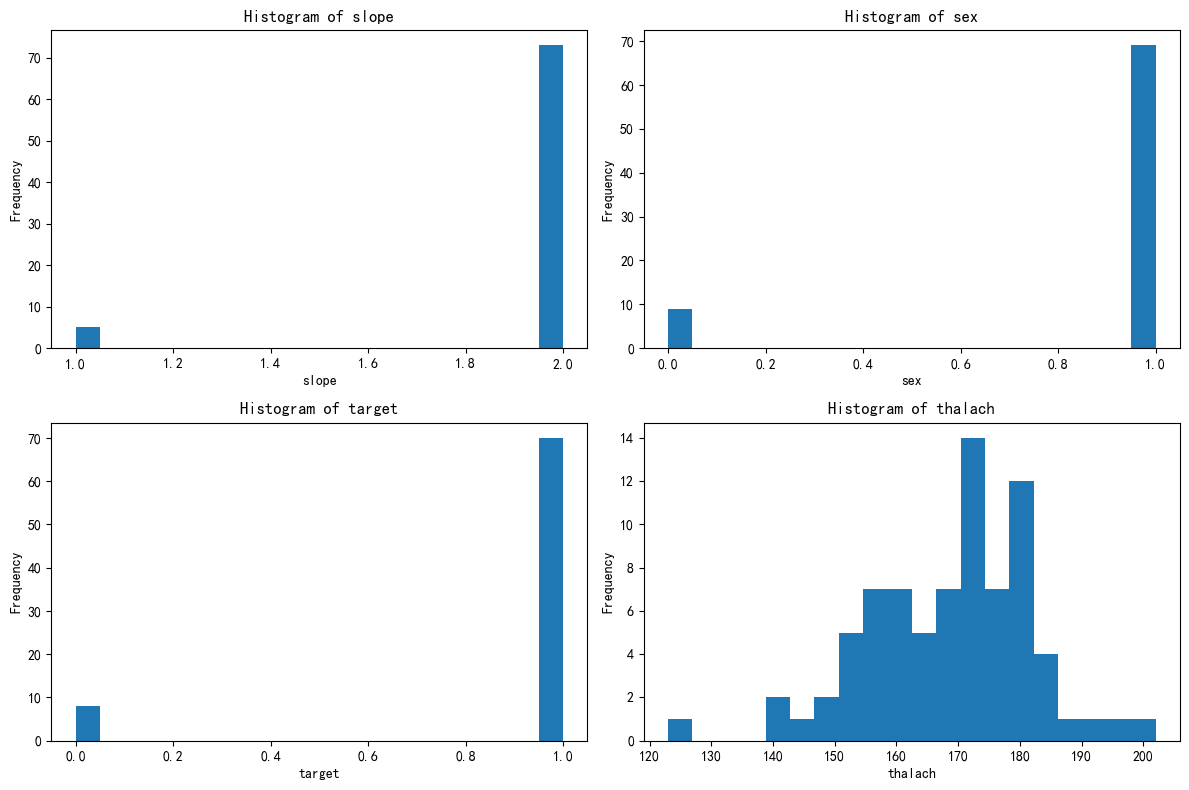
绘制簇0的分布图
# 先绘制簇0的分布图import matplotlib.pyplot as plt# 总样本中的前四个重要性的特征分布图
fig, axes = plt.subplots(2, 2, figsize=(12, 8))
axes = axes.flatten()for i, feature in enumerate(selected_features):axes[i].hist(X_cluster0[feature], bins=20)axes[i].set_title(f'Histogram of {feature}')axes[i].set_xlabel(feature)axes[i].set_ylabel('Frequency')plt.tight_layout()
plt.show()
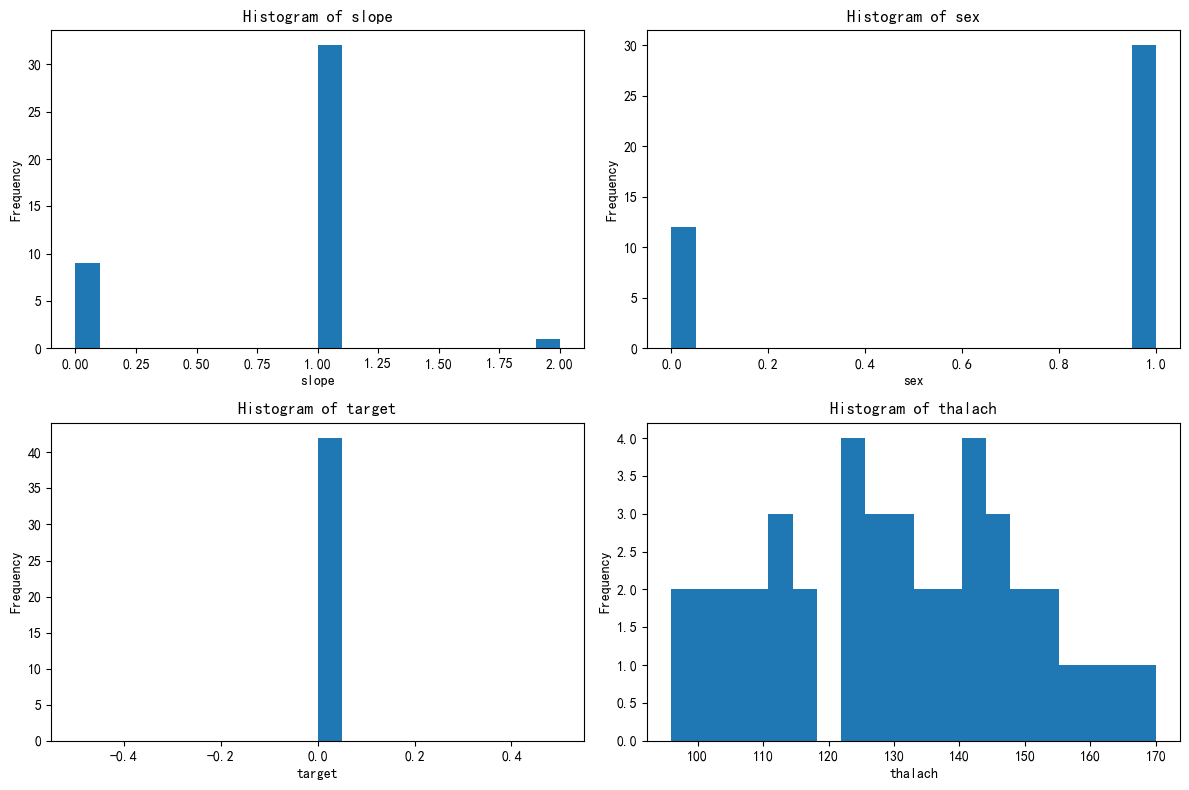
绘制簇1的分布图
# 绘制簇1的分布图import matplotlib.pyplot as plt# 总样本中的前四个重要性的特征分布图
fig, axes = plt.subplots(2, 2, figsize=(12, 8))
axes = axes.flatten()for i, feature in enumerate(selected_features):axes[i].hist(X_cluster1[feature], bins=20)axes[i].set_title(f'Histogram of {feature}')axes[i].set_xlabel(feature)axes[i].set_ylabel('Frequency')plt.tight_layout()
plt.show()
绘制簇2的分布图
# 先绘制簇2的分布图import matplotlib.pyplot as plt# 总样本中的前四个重要性的特征分布图
fig, axes = plt.subplots(2, 2, figsize=(12, 8))
axes = axes.flatten()for i, feature in enumerate(selected_features):axes[i].hist(X_cluster2[feature], bins=20)axes[i].set_title(f'Histogram of {feature}')axes[i].set_xlabel(feature)axes[i].set_ylabel('Frequency')plt.tight_layout()
plt.show()
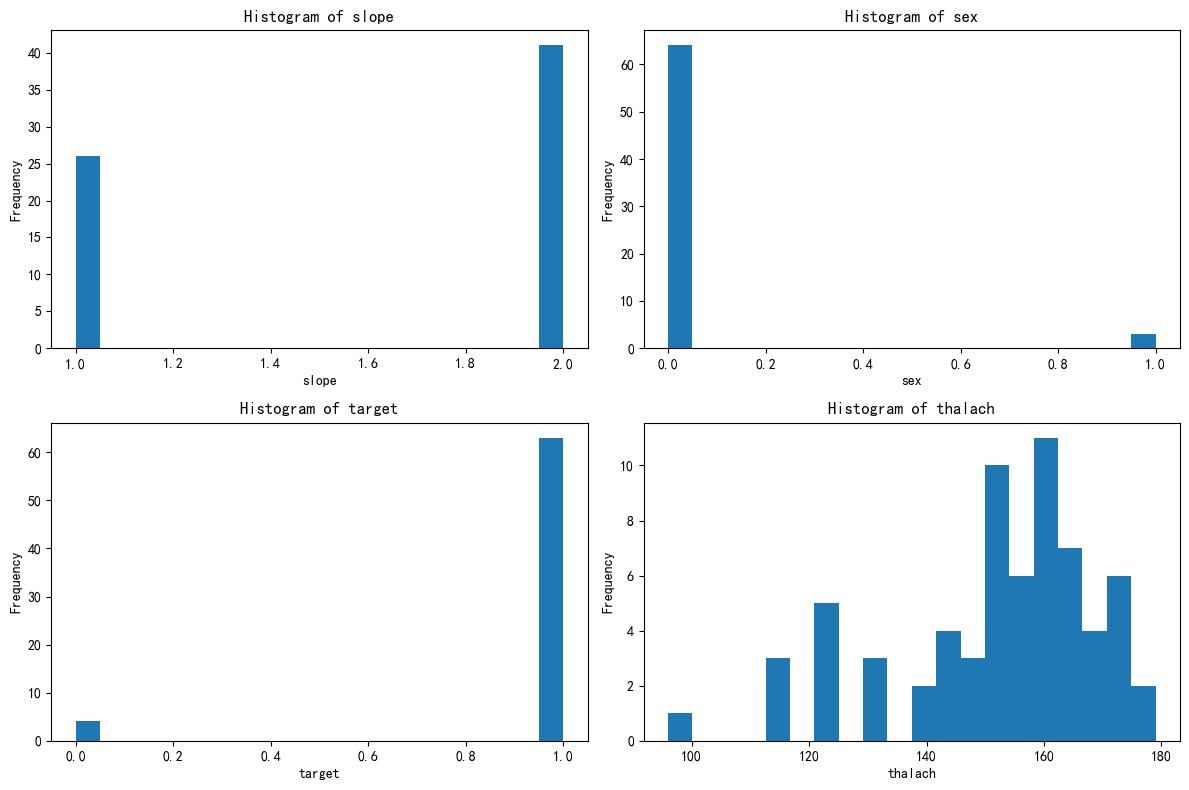
绘制簇3的分布图
# 先绘制簇3的分布图import matplotlib.pyplot as plt# 总样本中的前四个重要性的特征分布图
fig, axes = plt.subplots(2, 2, figsize=(12, 8))
axes = axes.flatten()for i, feature in enumerate(selected_features):axes[i].hist(X_cluster3[feature], bins=20)axes[i].set_title(f'Histogram of {feature}')axes[i].set_xlabel(feature)axes[i].set_ylabel('Frequency')plt.tight_layout()
plt.show()
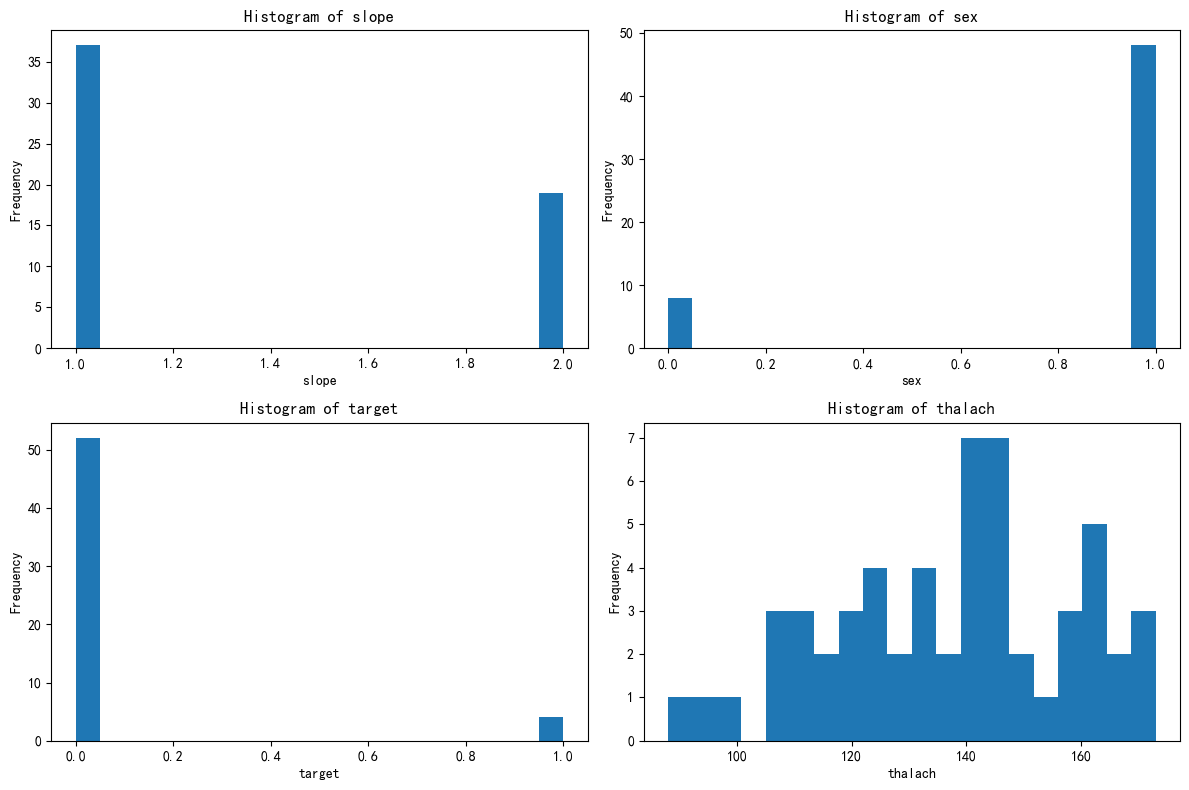
绘制簇4的分布图
# 先绘制簇4的分布图import matplotlib.pyplot as plt# 总样本中的前四个重要性的特征分布图
fig, axes = plt.subplots(2, 2, figsize=(12, 8))
axes = axes.flatten()for i, feature in enumerate(selected_features):axes[i].hist(X_cluster4[feature], bins=20)axes[i].set_title(f'Histogram of {feature}')axes[i].set_xlabel(feature)axes[i].set_ylabel('Frequency')plt.tight_layout()
plt.show()
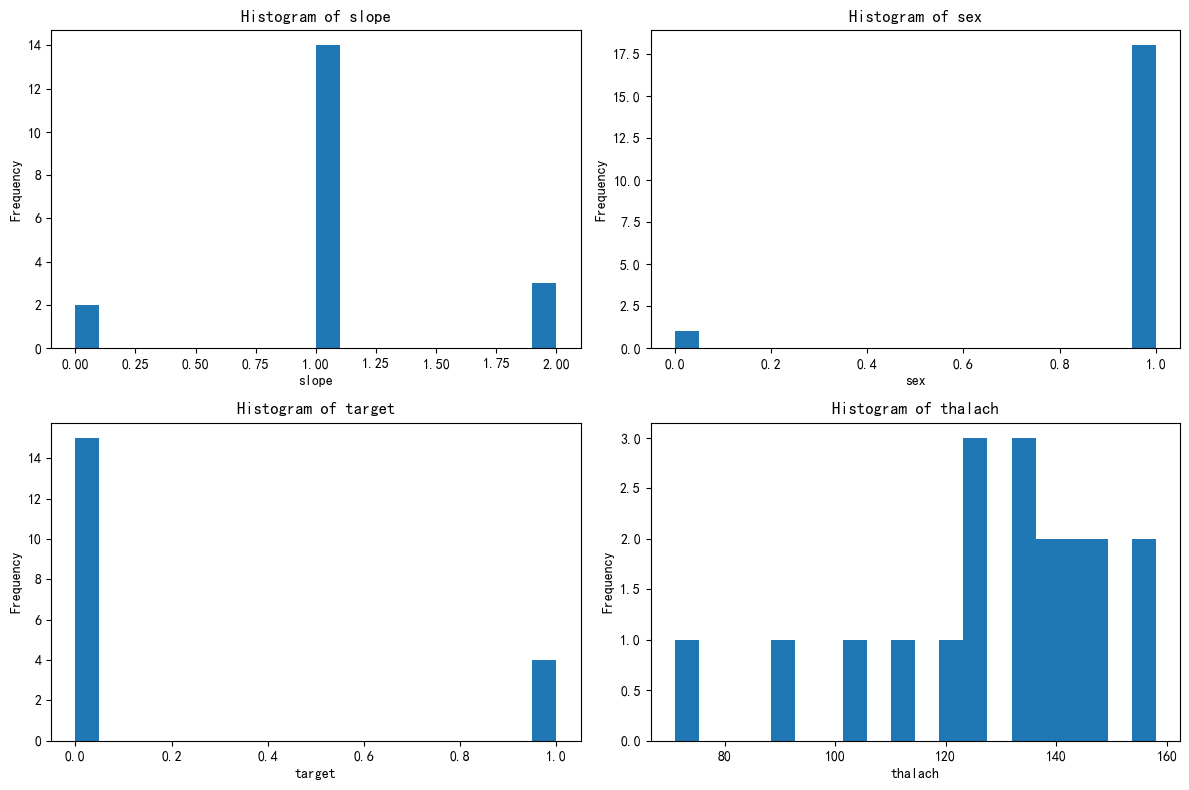
绘制簇5的分布图
# 先绘制簇5的分布图import matplotlib.pyplot as plt# 总样本中的前四个重要性的特征分布图
fig, axes = plt.subplots(2, 2, figsize=(12, 8))
axes = axes.flatten()for i, feature in enumerate(selected_features):axes[i].hist(X_cluster5[feature], bins=20)axes[i].set_title(f'Histogram of {feature}')axes[i].set_xlabel(feature)axes[i].set_ylabel('Frequency')plt.tight_layout()
plt.show()
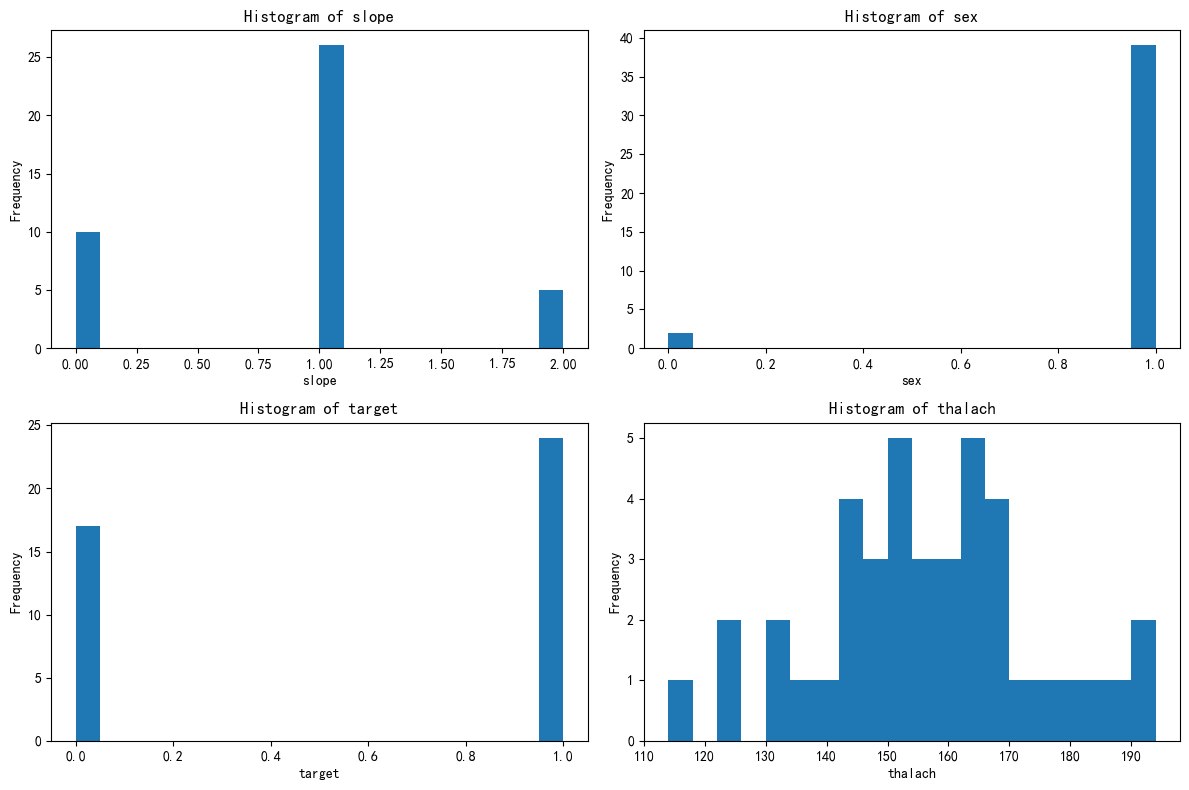
6个簇的总结与定义
5簇的含义
该簇代表高风险心脏病患者群体,典型特征为:
-
男性为主,心电图ST段斜率异常,确诊心脏病比例极高。
-
可能伴随心率异常(如运动耐受性差),需进一步临床干预。
4簇的含义
该簇代表低风险或健康人群,典型特征为:
-
女性为主,心电图ST段斜率正常,未确诊心脏病。
-
心率可能正常,无显著心脏疾病风险。
3簇类型推断:中等风险疑似病例
该簇很可能代表:
-
具有部分心脏病风险因素但未明确诊断的人群
-
或已确诊但症状较轻的心脏病患者
2推断簇的类型
-
健康男性簇:该簇主要由男性组成,且大多数为非心脏病患者。甲状腺体积在120-160之间,斜率特征在1.0和2.0附近有两个主要的集中区域。
该簇的含义可以总结为:
-
健康男性:该簇中的样本主要是健康的男性,甲状腺体积在正常范围内,斜率特征在1.0和2.0附近有两个主要的集中区域。
-
非心脏病患者:该簇中的样本大多数为非心脏病患者,表明这些特征组合与心脏病的发生没有显著关联。
1 推断簇的类型
根据上述特征分布,我们可以推断该簇的类型如下:
-
心脏病女性簇:该簇主要由女性组成,且大多数为心脏病患者。甲状腺体积在140-180之间,斜率特征在1.0和2.0附近有两个主要的集中区域。
该簇的含义可以总结为:
-
心脏病女性:该簇中的样本主要是心脏病女性,甲状腺体积在140-180之间,斜率特征在1.0和2.0附近有两个主要的集中区域。
-
心脏病患者:该簇中的样本大多数为心脏病患者,表明这些特征组合与心脏病的发生有显著关联。
0推断簇的类型
根据上述特征分布,我们可以推断该簇的类型如下:
-
健康男性簇:该簇主要由男性组成,且大多数为非心脏病患者。甲状腺体积在120-150之间,斜率特征主要集中在1.0附近。
该簇的含义可以总结为:
-
健康男性:该簇中的样本主要是健康的男性,甲状腺体积在120-150之间,斜率特征主要集中在1.0附近。
-
非心脏病患者:该簇中的样本大多数为非心脏病患者,表明这些特征组合与心脏病的发生没有显著关联。
@浙大疏锦行