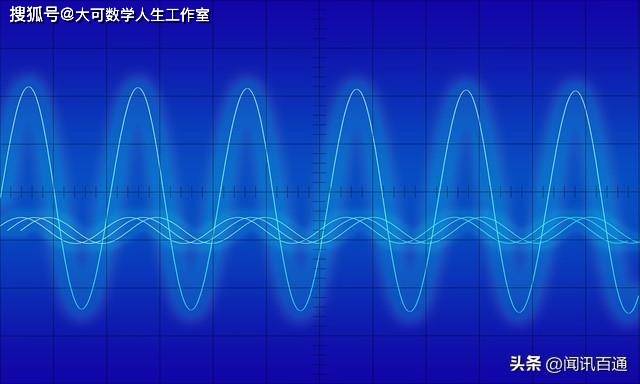
在当今数字化时代,音乐、图像和视频已经成为人们娱乐、沟通和表达的重要方式。而数学作为一门基础学科,也在其中扮演着重要角色,帮助我们更加深入地理解和处理这些数字资源。傅里叶分析、小波变换和计算机视觉等数学技术,既有助于音频、图像和视频的压缩、滤波和降噪,也对非平稳信号进行更加高效的分析。本文将就这些数学技术在音乐、图像和视频处理等领域的应用,进行深入剖析,让大家更好地了解数学在数字资源处理中的秘密。
基本概念
1.1 傅里叶分析
傅里叶分析的核心思想是将任何周期性信号分解成各种不同频率的正弦波,并用称为傅里叶级数的公式来表示。傅里叶级数由以下形式的表达式组成:
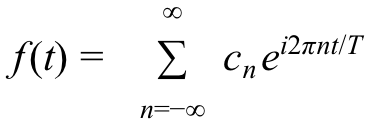
其中,f(t) 是周期为 T 的函数, 是称为傅里叶系数的复数,n 为频率,i 为虚数单位。该数学公式表示了一个与 f(t) 完全相同的周期信号,但由一系列正弦波组合而成。基于该理论,我们可以将任何复杂的信号分解为各个频率正弦波的组合,从而深入理解信号的特征。
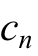
1.2 小波变换
小波变换是另一种将信号分解成短时间段(小波)的技术,可将信号分解为不同尺度的频带。小波变换使用一组名为小波基函数的函数族来完成这项任务。这些函数在时间和频率上都是局部化的,使得小波变换更适合分析非平稳信号和非线性信号。小波变换的数学表达式为:
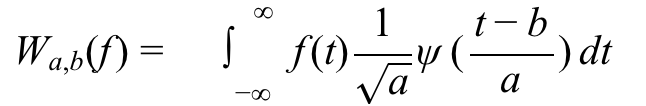
其中,f(t) 为被分析的信号,为小波基函数,a 和 b 分别表示尺度因子和时间平移因子。小波变换将信号分解成不同尺度和不同位置的小波,使我们能够检测到信号中的局部特征,例如信号的启动和停止时间、信号的频率分量等。
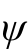
1.3 计算机视觉中的数学算法

计算机视觉是指使用计算机处理图像和视频数据,并从中提取有用信息的过程。计算机视觉中使用了许多数学算法,例如图像处理、模式识别、机器学习等。
在图像处理中,常用的数学技术包括卷积、傅里叶变换和小波变换等。通过这些技术,我们可以检测边缘、纹理和形状等图像的重要特征,并以此进行图像处理。例如,我们可以使用图像滤波技术来减少图像噪声,并使用图像分割技术来将图像分为不同的对象。
在模式识别中,数学算法可用于对图像和视频进行分类、目标检测和跟踪等任务。例如,在人脸识别中,我们可以使用数学算法来检测人脸的几何特征,并将这些特征与参考数据库中的图像进行比对。
在机器学习中,常用的数学技术包括统计学、线性代数和概率论等。例如,在深度学习中,我们可以使用神经网络来建立复杂模型,并使用反向传播算法来训练模型以实现准确的分类和预测。
应用实例
2.1 傅里叶分析在音乐处理中的应用

傅里叶分析是一种将信号分解成其组成频率的技术,可将音频信号分解成单个音调或音符的组合。通过对这些单个音符进行分析,我们可以找出声音中的重要元素并压缩音频流,减少存储和传输数据的需求。此外,傅里叶分析还可以用于音频信号的滤波和降噪,从而清除干扰和杂音,并提升音质。
傅里叶变换在图像处理中也有广泛的应用。通过傅里叶变换,我们可以将图像转换为频域表示,并按照重要性对频率进行排序。这使我们能够检测到图像中的重要特征,例如边缘、纹理和图案。此外,傅里叶变换还可以用于压缩图像,减少存储和传输数据的需求。
例子:音频信号的频谱分析
数学公式:
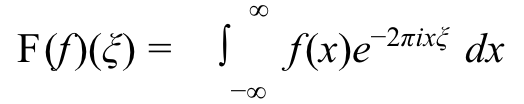
代码实现:
import numpy as np
from scipy.fft import fft, fftfreq
import matplotlib.pyplot as plt
# 生成音频信号
fs = 44100
t = np.linspace(0, 5, fs * 5, False)
x = np.sin(2 * np.pi * 440 * t) + 0.5 * np.sin(2 * np.pi * 880 * t)
# 进行傅里叶变换
X = fft(x)
freqs = fftfreq(len(x)) * fs
# 绘制频谱图
plt.plot(freqs, np.abs(X))
plt.xlabel('Frequency (Hz)')
plt.ylabel('Amplitude')
plt.show()
2.2 小波变换在图像处理中的应用
小波变换是一种将信号分解成短时间段(小波)的技术,可将图像信号分解为局部特征。相比于傅里叶变换,小波变换更适合分析非平稳信号和非线性信号。在图像处理中,小波变换可用于检测出图像中的局部特征,并且可以根据需要对不同的特征进行加权,从而实现特定的视觉效果。此外,小波变换还可以用于压缩和解压缩图像,以减少存储和传输数据的需求。
例子:图像压缩

数学公式:
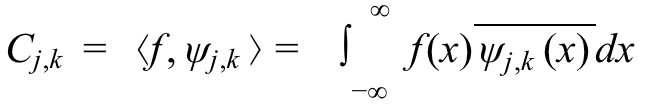
代码实现:
import pywt
import cv2
# 读取图像
img = cv2.imread('lena.jpg', cv2.IMREAD_GRAYSCALE)
# 进行小波变换,使用haar小波
coeffs = pywt.dwt2(img, 'haar')
# 将系数进行压缩
coeffs = list(coeffs)
coeffs[0] *= 0.1
coeffs[1] = tuple(map(lambda x: x * 0.1, coeffs[1]))
img_comp = pywt.idwt2(coeffs, 'haar')
# 显示原始图像和压缩后的图像
cv2.imshow('Original', img)
cv2.imshow('Compressed', img_comp.astype(np.uint8))
cv2.waitKey(0)
2.3 计算机视觉中的数学算法

计算机视觉是指利用计算机处理图像和视频数据,并从中提取有用的信息的过程。计算机视觉中使用了大量的数学算法,例如图像处理、模式识别、机器学习等。数学技术可以帮助我们理解图像和视频中的对象和模式,并通过量化这些特征来实现自动分类、识别和跟踪等任务。
例如,在人脸识别领域,计算机视觉可以使用数学算法来分析人脸的几何特征,并将这些特征与参考数据库中的图像进行比对。在自动驾驶领域中,计算机视觉可以使用数学算法来分析道路和汽车周围的物体,从而实现自动驾驶。
例子:使用卷积神经网络(CNN)进行图像分类
举例
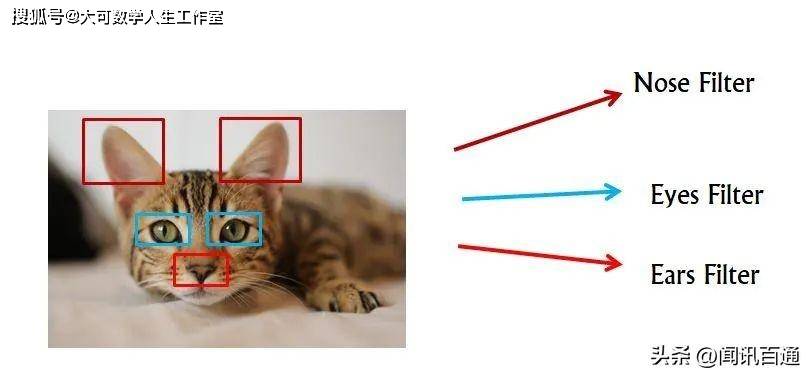
数学公式:
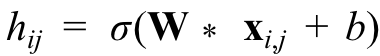
代码实现:
import tensorflow as tf
from tensorflow.keras.datasets import mnist
from tensorflow.keras.layers import Conv2D, MaxPooling2D, Flatten, Dense, Dropout
from tensorflow.keras.models import Sequential
# 加载数据集
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()
# 数据预处理
train_images = train_images.reshape((60000, 28, 28, 1))
train_images = train_images.astype('float32') / 255
test_images = test_images.reshape((10000, 28, 28, 1))
test_images = test_images.astype('float32') / 255
# 建立模型
model = Sequential([
Conv2D(32, (3, 3), activation='relu', input_shape=(28, 28, 1)),
MaxPooling2D((2, 2)),
Conv2D(64, (3, 3), activation='relu'),
MaxPooling2D((2, 2)),
Conv2D(64, (3, 3), activation='relu'),
Flatten(),
Dense(64, activation='relu'),
Dropout(0.5),
Dense(10, activation='softmax')
])
# 模型编译
model.compile(optimizer='adam',
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
# 训练模型
model.fit(train_images, train_labels, epochs=5)
# 测试模型
test_loss, test_acc = model.evaluate(test_images, test_labels)
print('Test accuracy:', test_acc)
结论
总之,数学在音乐、图像和视频处理中具有重要的应用价值,这些技术的发展不断推进着这些领域的研究和应用。傅里叶分析、小波变换和计算机视觉等数学技术,在音频、图像和视频处理等领域都发挥着重要的作用。未来我们可以期待更多的数学技术被应用于数字资源处理中,这将使得数字尽可能地逼真,并更加符合人们的感性认知。
来自:闻讯百通