任务19：实现山东省气温预测-海口c网

任务描述

知识点：

时间序列分析

重点：

指数平滑法
ARIMA模型
Python连接数据库，查询数据

内容：

读取并创建时序数据
使用指数平滑法建立模型，并预测下一年山东省各月的平均气温
使用ARIMA建立模型，并预测下一年山东省各月的平均气温
对比两种模型的优劣
将预测的数据更新到数据库中

任务指导

1. 读取并创建时序数据

数据集为2000年1月到2020年12月每月各省的平均气温数据（数据存于MySQL数据库中，数据库为china_all，存于province_temp_all表中）。
读取数据后，建立时间索引的序列数据。
通过图形查看数据的特征。

2. 使用指数平滑法建立模型，并预测下一年各月的最低气温

根据数据的特征，建立相应的指数平滑法模型。
创建该模型的拟合图
对模型效果进行评估
预测下一年各月的最低气温

3. 使用ARIMA建立模型，并预测下一年各月的最低气温

根据数据的特征，对数据进行差分使数据平稳。
找到ARIMA模型的最优参数
根据最优参数建立ARIMA模型
对模型效果进行评估
预测下一年各月的最低气温
将指数平滑法预测的2023年各月的山东气温数据更新到province_temp数据库表中

任务实现

1. 读取并创建时序数据

1）安装pymysql和sqlalchemy库

可以打开anaconda自带的Prompt或Windows的cmd，输入如下：

pip install pymysql sqlalchemy

如果下载速度过慢，推荐使用国内镜像，如下：

pip install -i https://pypi.tuna.tsinghua.edu.cn/simple/ pymysql sqlalchemy

2）引入相应的库

from sqlalchemy import create_engine,text
import pandas as pd
import numpy as np
from statsmodels.tsa import holtwinters as hw
from statsmodels.graphics.tsaplots import plot_acf,plot_pacf
from statsmodels.tsa.stattools import adfuller
from statsmodels.graphics.gofplots import qqplot
import matplotlib.pyplot as plt
from statsmodels.tsa.arima.model import ARIMA
import warnings
warnings.filterwarnings('ignore')

3）读取数据，建立时序数据

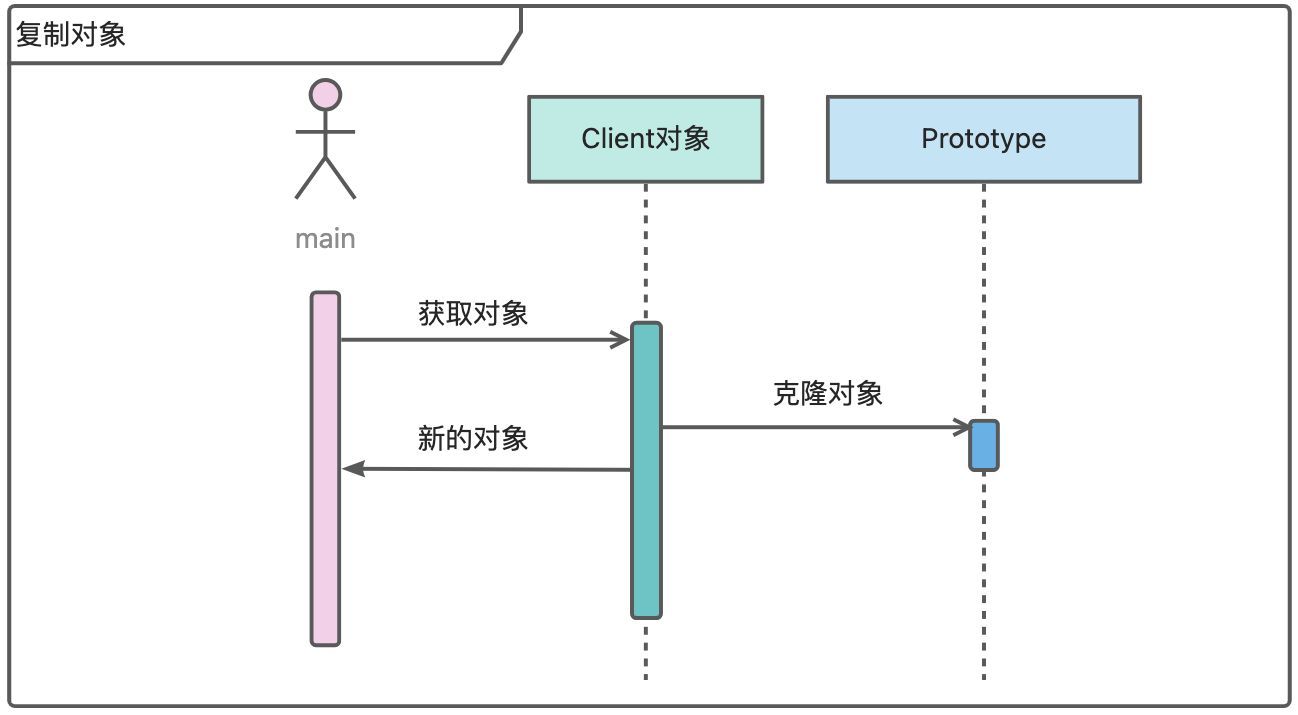
SQLAlchemy是一个基于Python实现的orm框架，该框架建立在DB API之上，使用关系对象映射进行数据库操作，简而言之是：将类和对象转换成SQL，然后使用数据API执行SQL并获取执行结果，是第三方的orm框架，可以独立于web项目使用。

SQLAlchemy本身无法操作数据库，其必须以来pymysql等第三方插件，Dialect用于和数据API进行交流，根据配置文件的不同调用不同的数据库API，从而实现对数据库的操作，如：mysql+pymysql://<username>:<password>@<host>/<dbname>]。

数据存于MySQL数据库中，数据库为china_all，存于province_temp_all表中。

数据库安装在Master环境中，各参数如下：

username：root

password：root

host：192.168.4.190:3306（备注：3306为数据库服务默认的端口，前面的ip需要根据自己的实际环境进行修改）

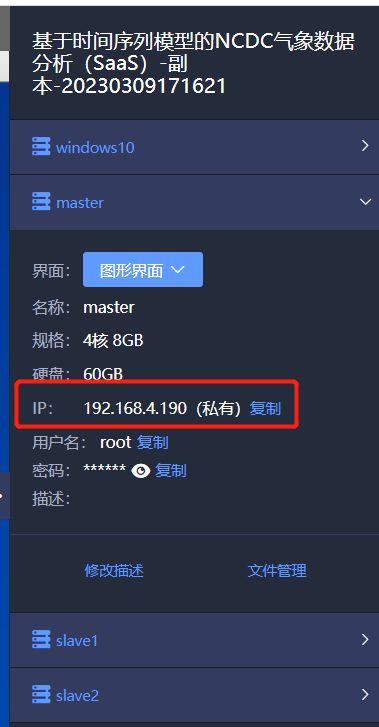
dbname：province_temp_all

engine=create_engine('mysql+pymysql://root:root@192.168.4.190:3306/china_all')
sql=text('select * from province_temp_all')
connect = engine.connect()
mydata=pd.read_sql(sql,connect)
print(mydata.info())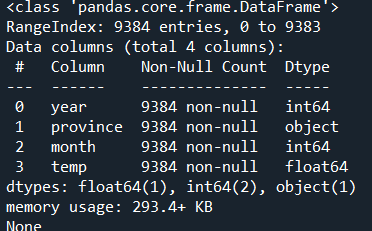

可以看到，数据共有9384行4列。

print(mydata.head())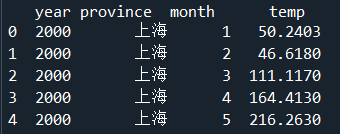

获取山东省平均气温数据

temp_sd=mydata[mydata['province']=='山东']
print(temp_sd.head())

建立时序数据。温度的数据膨胀因子为10，因此在处理温度时应除以10来还原。

date=pd.period_range('2000/01',periods=len(temp_sd),freq='M')
temp_data=pd.DataFrame(temp_sd['temp'].values/10,index=date,columns=['temp'])
print(temp_data.head())
print(temp_data.tail())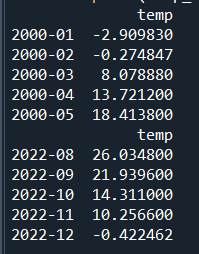

可以看到，数据为2000年1月到2022年12月的平均温度数据

绘制时序图

temp_data.plot()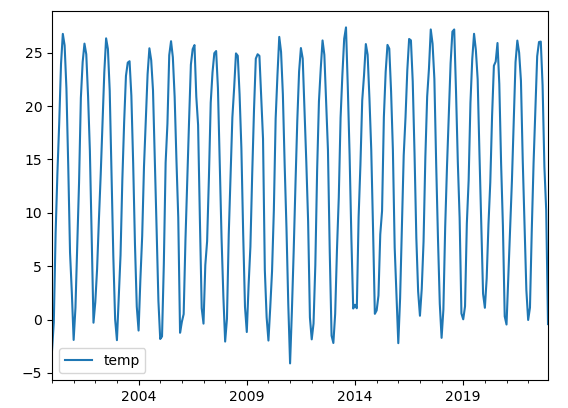

从图中可以看到，平均气温的趋势性几乎没有，但是存在季节性，即每年的7、8月份左右存在波峰，12、1月份存在波谷。因此可以用相加的模型来处理。

2. 使用指数平滑法建立模型，并预测下一年各月的最低气温

1）建立指数平滑法模型。

hw_model=hw.ExponentialSmoothing(temp_data,trend='add',seasonal='add',seasonal_periods=12).fit()
print(hw_model.summary())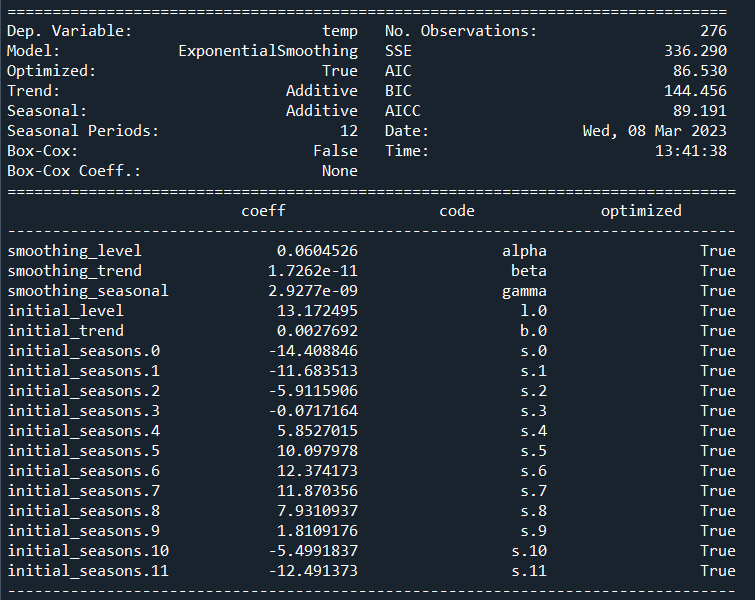

可以看到，α、β、γ的估计值分别是 0.06,1.7262e-11 和2.9277e-09。 α 是非常低，意味着在当前时间点估计得水平是基于历史观测值。 beta 的估计值是接近0.00，表明估计出来的趋势部分的斜率在整个时间序列上是不变的，并且应该是等于其初始值。直观的感觉，水平改变非常多，但是趋势部分的斜率b却仍然是大致相同的。同样gamma 的值（接近为0）表明当前时间点的季节性部分的估计基于历史观测值。

2）创建该模型的拟合图

temp_data.plot()
hw_model.fittedvalues.plot(label='fitted_values',legend=True)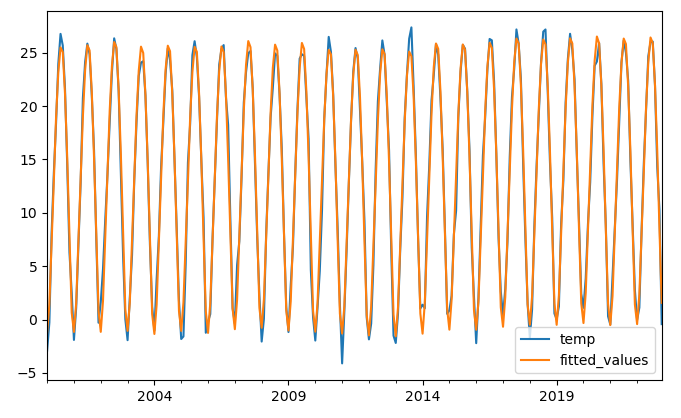

3）对模型效果进行评估

查看残差自相关图

plot_acf(hw_model.resid)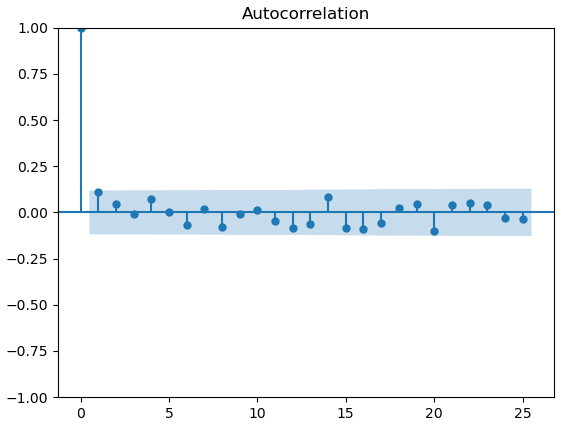

可以看到，残差滞后20阶的自相关系数都在标准范围内，说明残差几乎没有自相关。

残差平稳性检验

adfuller(hw_model.resid)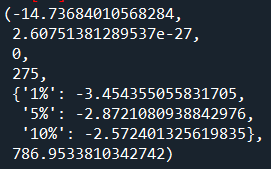

可以看到，p值非常小，几乎为0，说明残差是平稳序列。

#残差正态性
plt.figure()
plt.hist(hw_model.resid,density=True)
hw_model.resid.plot(kind='kde')
plt.show()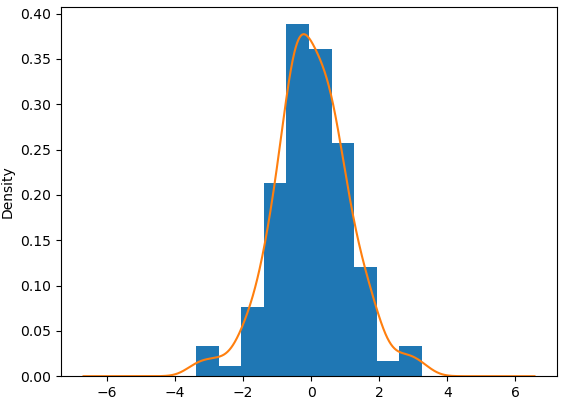

qqplot(hw_model.resid,line='s')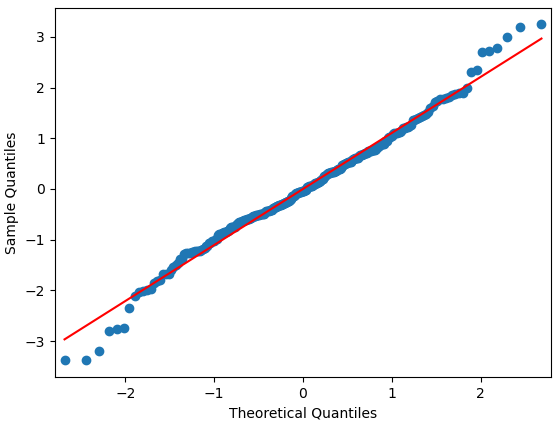

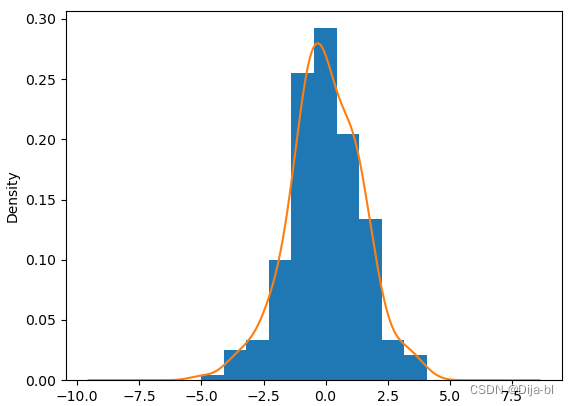
从直方图、核密度图和正态QQ图可以看到，残差几乎服从正态分布。

4）预测下一年各月的平均气温

temp_forecast1=hw_model.predict(start='2023/01',end='2023/12')
print(temp_forecast1)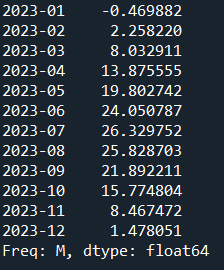

绘图

temp_data.plot()
temp_forecast1.plot(label='forecast',legend=True)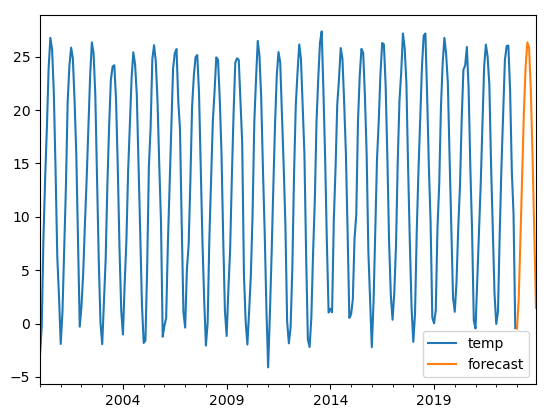

3. 使用ARIMA建立模型，并预测下一年各月的气温

1）根据数据的特征，对数据进行差分使数据平稳。

temp_data_diff1=temp_data.diff(12).dropna()   #去除季节性
temp_data_diff2=temp_data_diff1.diff().dropna()
temp_data_diff2.plot()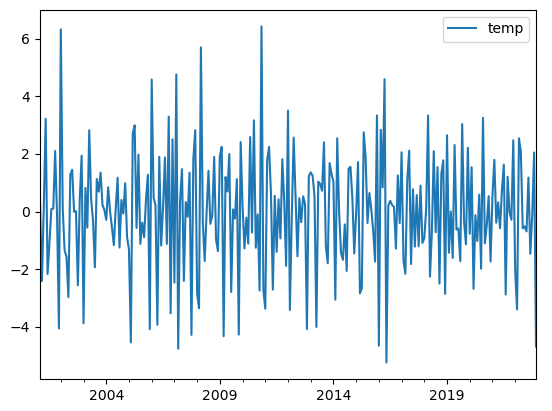

从图形上看，数据已经趋于平稳

单位根检验

adfuller(temp_data_diff2['temp'])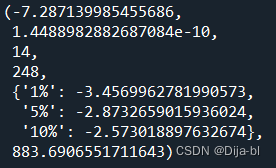

可以看到，p值非常小，几乎为0，说明数据已经是平稳序列。

2）找到ARIMA模型的最优参数

通过自相关和偏自相关图形寻找

plot_acf(temp_data_diff2)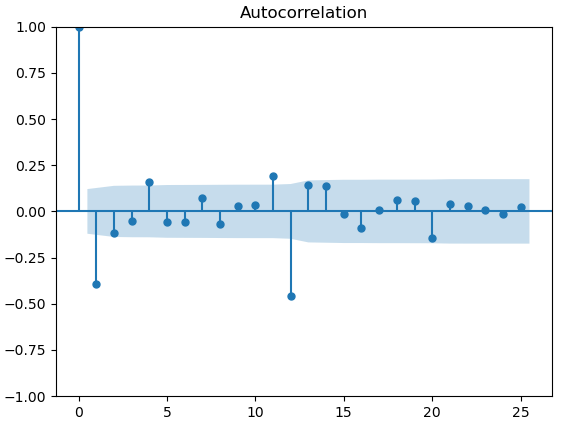

plot_pacf(temp_data_diff2)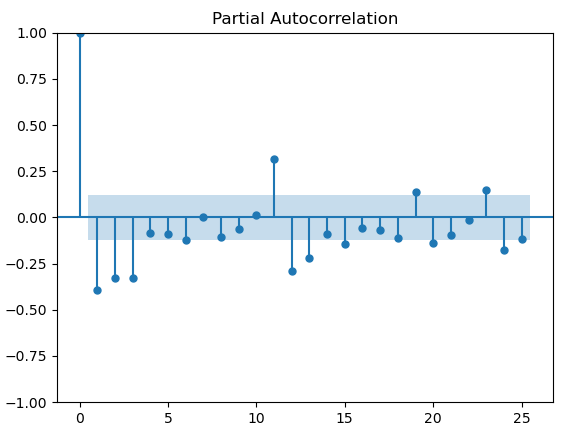

通过acf图，定q=1，通过pacf，定p=3，因此ARIMA模型的参数为ARIMA(3,1,1)

通过循环寻找最优参数

index=0
parma_df=pd.DataFrame(columns=['p','d','q','AIC'])
for p in range(6):for q in range(6):        try:myfit=ARIMA(temp_data_diff1,order=(p,1,q)).fit()parma_df.loc[index]=[p,1,q,myfit.aic]index+=1except:passmin_param=parma_df.loc[parma_df['AIC'].idxmin()]
print(parma_df)
print('最优的参数为index=%d,p=%d,d=1,q=%d,AIC=%f.2'%(min_param.name,min_param['p'],min_param['q'],min_param['AIC']))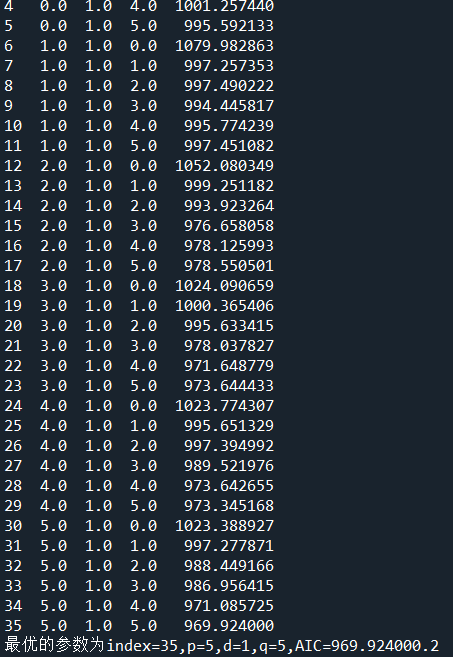

可以看到，最优的p、q值为第35个，p=5，q=5。

3）根据最优参数建立ARIMA模型

arima_model=ARIMA(temp_data_diff1,order=(5,1,5)).fit()
print(arima_model.summary())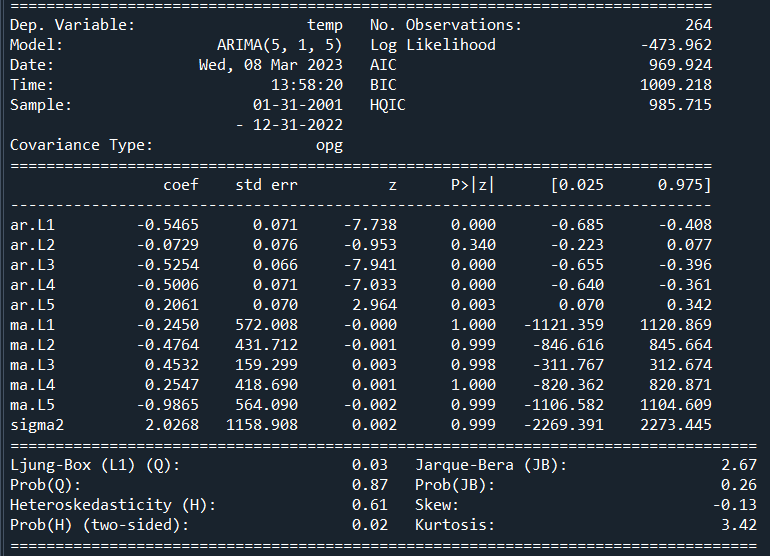

返回一份格式化的模型报告，包含模型的系数、p值、AIC和BIC等详细指标。

查看拟合图

#还原季节差分
temp_fittedvalues=temp_data.shift(12,freq='M')['temp']+arima_model.fittedvalues
temp_data.plot()
temp_fittedvalues.plot(label='fitted_values',legend=True)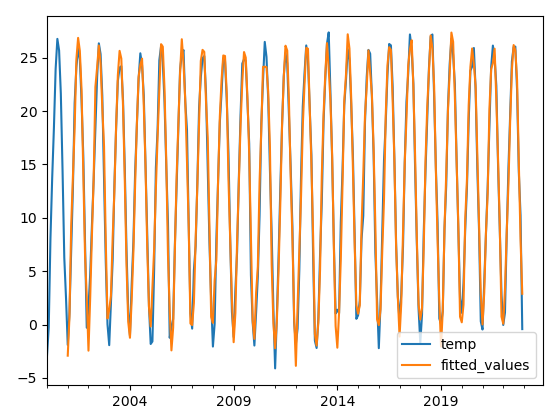

4）对模型效果进行评估

#残差自相关图
plot_acf(arima_model.resid)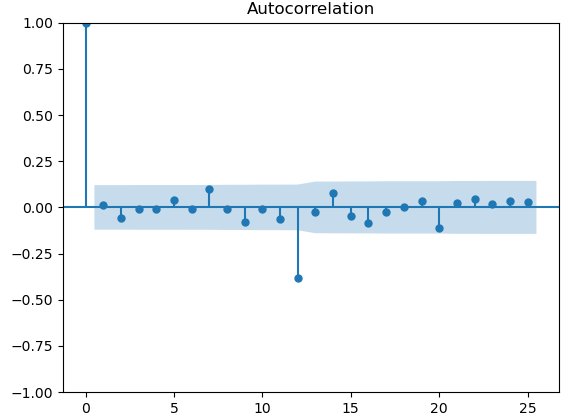

在残差滞后20阶的自相关图可以看到，自相关系数都在标准范围内，均接近于0，说明残差基本没有自相关性

残差平稳性检验

adfuller(arima_model.resid)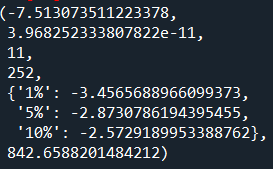

可以看到，通过单位根检验，可以看到p值接近0，不存在单位根，因此可以认为残差序列是平稳的。

残差正态性

plt.figure()
plt.hist(arima_model.resid,density=True)
arima_model.resid.plot(kind='kde')
plt.show()

qqplot(arima_model.resid,line='s')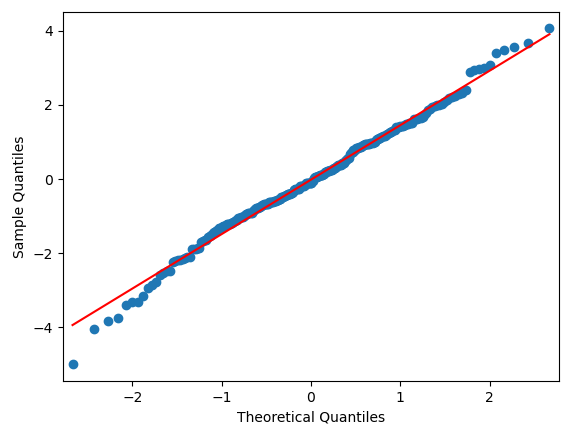

从直方图、

核密度图和正态QQ图可以看到，残差几乎服从正态分布。

5）预测下一年各月的最低气温

temp_forecast_diff1=arima_model.forecast(12)
print(temp_forecast_diff1)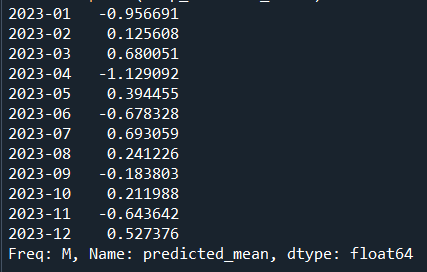

还原季节差分

temp_forecast=temp_data.iloc[-12:,:].shift(12,freq='M')['temp']+temp_forecast_diff1
print(temp_forecast)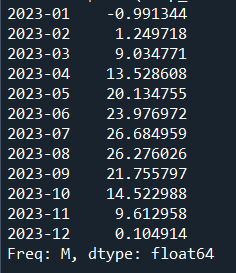

绘图

temp_data.plot()
temp_forecast.plot(label='forecast',legend=True)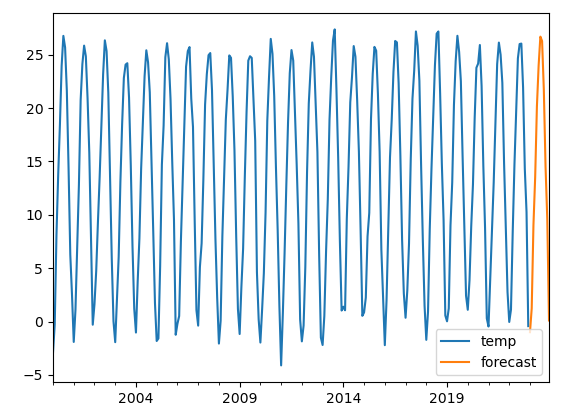

4. 比较两种模型的优劣

#指数平滑法RMSE
hw_mse=np.power(temp_data['temp'].iloc[12:,].values-hw_model.fittedvalues.iloc[12:,].values,2).mean()
hw_rmse=np.sqrt(hw_mse)
#ARIMA模型RMSE
arima_mse=np.power(temp_data['temp'].iloc[12:,].values-temp_fittedvalues.iloc[:-12,].values,2).mean()
arima_rmse=np.sqrt(arima_mse)
print('指数平滑法RMSE为%.4f，ARIMA模型RMSE为%.4f'%(hw_rmse,arima_rmse))

通过比较指数平滑法和ARIMA的同期数据计算的RMSE（均方根误差），可以看到指数平滑法的RMSE更小，因此，指数平滑法的模型精度更高。

5. 将预测的数据更新到数据库中

在province_temp表中，存了各省份1-12月的平均气温和预测气温，预测气温为0。

先查看province_temp表中山东的数据，（需要进入mysql）如下：

select * from province_temp where province="山东";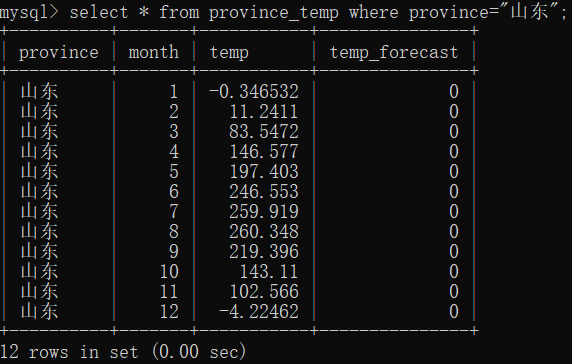

然后继续在Spyder中，通过前面的指数平滑法预测后，将预测的数据更新到数据库表中

for i in range(len(temp_forecast1)):mytext='update province_temp set temp_forecast=%.4f where province="山东" and month=%d' % (temp_forecast1[i],i+1)sql=text(mytext)connect = engine.connect()connect.execute(sql)

运行以上代码块，然后在MySQL中查看山东的气温数据，如下：