2.正切函数图像

3.三角函数的图像与性质

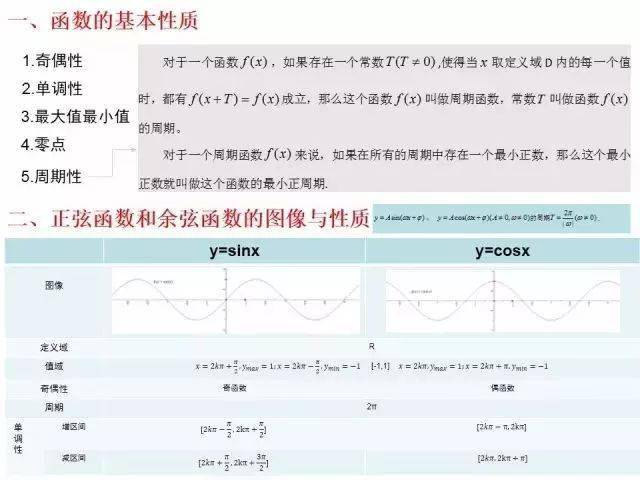
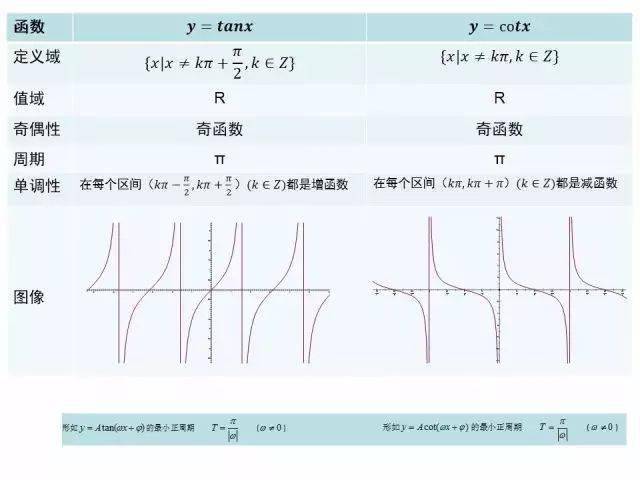
4.主要研究方法

5.主要内容

三角函数解题技巧

三角函数是高考数学核心考点之一。

它侧重于考查学生的观察能力、思维能力和综合分析能力，在高考试题中始终保持"一大一小"甚至是"一大两小"的模式。

01

见“给角求值”问题，运用“新兴”诱导公式一步到位转换到区间(-90o，90o)的公式

1、sin(kπ+α)=(-1)ksinα(k∈Z)；

2、cos(kπ+α)=(-1)kcosα(k∈Z)；

3、 tan(kπ+α)=(-1)ktanα(k∈Z)；

4、cot(kπ+α)=(-1)kcotα(k∈Z).

02

见“sinα±cosα”问题，运用三角“八卦图”

1、sinα+cosα>0(或<0)óα的终边在直线y+x=0的上方(或下方)；

2、sinα-cosα>0(或<0)óα的终边在直线y-x=0的上方(或下方)；

3、|sinα|>|cosα|óα的终边在Ⅱ、Ⅲ的区域内；

4、|sinα|<|cosα|óα的终边在Ⅰ、Ⅳ区域内.

03

见“知1求5”问题，造Rt△，用勾股定理，熟记常用勾股数(3，4，5)，(5，12，13)，(7，24，25)，仍然注意“符号看象限”。

04

见“切割”问题，转换成“弦”的问题。

05

“见齐思弦”=>“化弦为一”：已知tanα，求sinα与cosα的齐次式，有些整式情形还可以视其分母为1，转化为sin2α+cos2α.

06

见“正弦值或角的平方差”形式，启用“平方差”公式

1、sin(α+β)sin(α-β)= sin2α-sin2β；

2、 cos(α+β)cos(α-β)= cos2α-sin2β.

07

见“sinα±cosα与sinαcosα”问题，启用平方法则

(sinα±cosα)2=1±2sinαcosα=1±sin2α，故

1、若sinα+cosα=t，(且t2≤2)，则2sinαcosα=t2-1=sin2α；

2、若sinα-cosα=t，(且t2≤2)，则2sinαcosα=1-t2=sin2α.

08

见“tanα+tanβ与tanαtanβ”问题，启用变形公式

tanα+tanβ=tan(α+β)(1-tanαtanβ).思考：tanα-tanβ=？？？

09

见三角函数“对称”问题，启用图象特征代数关系：(A≠0)

1、函数y=Asin(wx+φ)和函数y=Acos(wx+φ)的图象，关于过最值点且平行于y轴的直线分别成轴对称；

2、函数y=Asin(wx+φ)和函数y=Acos(wx+φ)的图象，关于其中间零点分别成中心对称；

3、同样，利用图象也可以得到函数y=Atan(wx+φ)和函数y=Acot(wx+φ)的对称性质。

10

十、见“求最值、值域”问题，启用有界性，或者辅助角公式

1、|sinx|≤1，|cosx|≤1；

2、(asinx+bcosx)2=(a2+b2)sin2(x+φ)≤(a2+b2)；

3、asinx+bcosx=c有解的充要条件是a2+b2≥c2.

11

见“高次”，用降幂，见“复角”，用转化

1、cos2x=1-2sin2x=2cos2x-1.

2、2x=(x+y)+(x-y)；

2y=(x+y)-(x-y)；x-w=(x+y)-(y+w)等。

正弦函数、余弦函数、正切函数和余切函数统称为三角函数。它们的地位和作用与一次函数、二次函数、幂函数、指数函数以及对数函数一样，都是基本初等函数。

二

三角函数题型

三角函数的图像和性质是高考的热点，也是大家在必修四学习的重点，这一模块题型复杂多样，思路扑朔迷离，技巧应用多变，下面对三角函数性质及其应用所涉及的题型稍作梳理，供大家学习参考.

题型一

三角函数求定义域问题

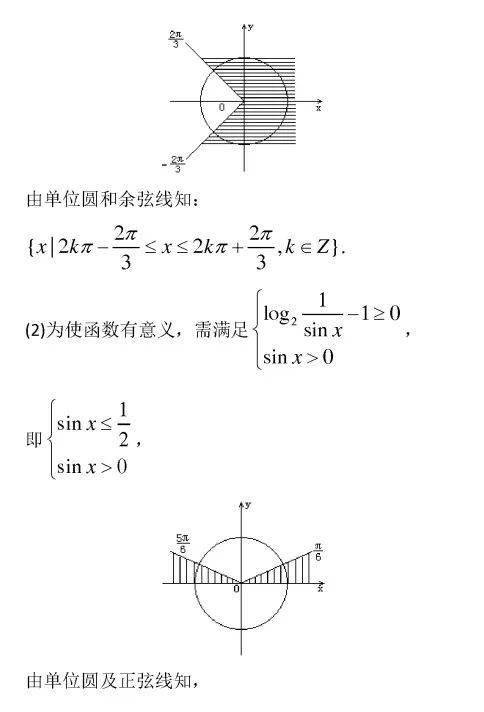
【解题指导】在求解涉及三角函数的定义域问题，特别是求综合性较强的三角函数的定义域，我们同样可以利用“数形结合”，在单位圆中画三角函数线，利用三角函数的定义及三角函数线表示三角不等式的解集，然后把多个不等式取交集的问题转化成表示不等式解集的扇形区域的交集来完成．如果和数集取交集，则对k赋值，利用数轴画线求交集的方法进行. 求三角函数的定义域要注意三角函数本身的特征和性质，如在转化为不等式或不等式组后要注意三角函数的符号及单调性，在进行三角函数的变形时，要注意三角函数的每一步变形都保持恒等，即不能改变原函数的自变量的取值范围．

题型二

三角函数的值域或最值

题型三

三角函数的周期性

题型四

函数的单调区间

▼

三角函数的图像和性质是高考的热点，也是大家在必修四学习的重点，这一模块题型复杂多样，思路扑朔迷离，技巧应用多变，下面继续对三角函数性质及其应用所涉及的题型稍作梳理，供大家学习参考.

题型五

由图像求三角函数的解析式

题型六

三角函数的奇偶性应用

（1）判断函数的奇偶性，应先判定函数定义域的对称性，注意偶函数的和、差、积、商仍为偶函数；复合函数在复合过程中，对每个函数而言，“同奇才奇、一偶则偶”．一般情况下，需先对函数式进行化简，再判断其奇偶性；

题型七

三角函数的对称性应用

题型八

与x轴的交点问题

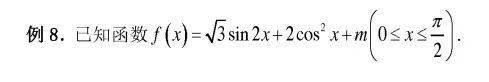
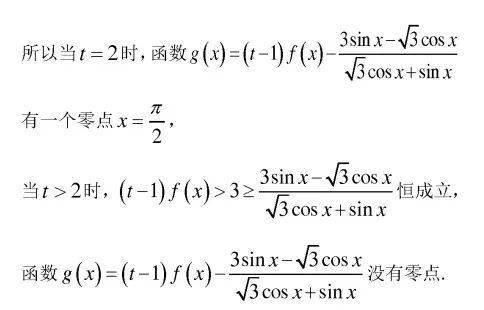
【名师叮嘱】三角函数有关函数零点的问题一般都转化为两个函数图像的交点问题，数形结合，根据图像列不等式求解参数的范围，解题时要注意所研究的角的范围.

解决三角函数的11种方法

三角函数的各类问题，由于涉及的三角公式较多，问题的解法也比较灵活，但也会呈现出一定的规律性，本文拟对其中的解题方法进行总结归纳．

1

凑角法

一些求值问题通过观察角之间的关系，并充分利用角之间的关系，往往是凑出特殊角，可以实现顺利解答。

2

降幂法

3

对偶法

根据一些三角式的特征，适当进行配对，有时可以实现问题的顺利解答。

4

换元法

给值求值问题都是给的单角的某一三角函数值，利用换元法可以将问题转化为熟悉的已知单角的三角函数值求值（包括求周期、对称轴、对称中心等）问题。

5

方程法

有时可以根据已知构造所求量的方程解答。

6

讨论法

涉及含有参数或正负情形的三角问题，往往需要借助讨论法进行解答。

7

平方法

分析已知和所求，有时借助“取平方”的方法可以实现顺利解题。

8

猜想法

有时根据已知数据的特征进行必要的猜想，能更好的解决求值问题。

9

图象法

有时候，借助图象才能更好的解决对应的三角函数问题。

10

比例法

借助比例的性质，有时可以实现快速解答三角函数问题。

11

构造三角形法

名师堂学校西博源校区: 府后西街中港花苑2 号楼（西博源超市北，中国银行顶层），2 、5 、13 、17、19、20、101、201、302、303、307、310路公交车经过

名师堂学校西博源校区: 府后西街中港花苑2 号楼（西博源超市北，中国银行顶层），2 、5 、13 、17、19、20、101、201、302、303、307、310路公交车经过