文章目录
- 题目
- 标题和出处
- 难度
- 题目描述
- 要求
- 示例
- 数据范围
- 前言
- 解法
- 思路和算法
- 代码
- 复杂度分析
题目
标题和出处
标题:二维区域和检索 - 矩阵不可变
出处:304. 二维区域和检索 - 矩阵不可变
难度
5 级
题目描述
要求
给定一个二维矩阵 matrix \texttt{matrix} matrix,处理以下类型的多个查询:
- 计算以 (row1, col1) \texttt{(row1, col1)} (row1, col1) 为左上角、 (row2, col2) \texttt{(row2, col2)} (row2, col2) 为右下角的子矩阵元素的和。
实现 NumMatrix \texttt{NumMatrix} NumMatrix 类:
- NumMatrix(int[] matrix) \texttt{NumMatrix(int[] matrix)} NumMatrix(int[] matrix) 使用矩阵 matrix \texttt{matrix} matrix 初始化对象。
- int sumRegion(int row1, int col1, int row2, int col2) \texttt{int sumRegion(int row1, int col1, int row2, int col2)} int sumRegion(int row1, int col1, int row2, int col2) 返回矩阵 matrix \texttt{matrix} matrix 中的以 (row1, col1) \texttt{(row1, col1)} (row1, col1) 为左上角、 (row2, col2) \texttt{(row2, col2)} (row2, col2) 为右下角的子矩阵元素的和。
要求 sumRegion \texttt{sumRegion} sumRegion 的时间复杂度是 O(1) \texttt{O(1)} O(1)。
示例
示例 1:
输入:
["NumMatrix", "sumRegion", "sumRegion", "sumRegion"] \texttt{["NumMatrix", "sumRegion", "sumRegion", "sumRegion"]} ["NumMatrix", "sumRegion", "sumRegion", "sumRegion"]
[[[[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]], [2, 1, 4, 3], [1, 1, 2, 2], [1, 2, 2, 4]] \texttt{[[[[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]], [2, 1, 4, 3], [1, 1, 2, 2], [1, 2, 2, 4]]} [[[[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]], [2, 1, 4, 3], [1, 1, 2, 2], [1, 2, 2, 4]]
输出:
[null, 8, 11, 12] \texttt{[null, 8, 11, 12]} [null, 8, 11, 12]
解释:
NumMatrix numMatrix = new NumMatrix([[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]); \texttt{NumMatrix numMatrix = new NumMatrix([[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]);} NumMatrix numMatrix = new NumMatrix([[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]);
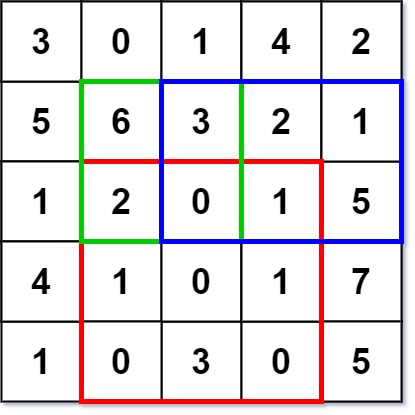
numMatrix.sumRegion(2, 1, 4, 3); \texttt{numMatrix.sumRegion(2, 1, 4, 3);} numMatrix.sumRegion(2, 1, 4, 3); // 返回 8 \texttt{8} 8(红色矩形框的元素和)
numMatrix.sumRegion(1, 1, 2, 2); \texttt{numMatrix.sumRegion(1, 1, 2, 2);} numMatrix.sumRegion(1, 1, 2, 2); // 返回 11 \texttt{11} 11(绿色矩形框的元素和)
numMatrix.sumRegion(1, 2, 2, 4); \texttt{numMatrix.sumRegion(1, 2, 2, 4);} numMatrix.sumRegion(1, 2, 2, 4); // 返回 12 \texttt{12} 12(蓝色矩形框的元素和)
数据范围
- m = matrix.length \texttt{m} = \texttt{matrix.length} m=matrix.length
- n = matrix[i].length \texttt{n} = \texttt{matrix[i].length} n=matrix[i].length
- 1 ≤ m, n ≤ 200 \texttt{1} \le \texttt{m, n} \le \texttt{200} 1≤m, n≤200
- -10 5 ≤ matrix[i][j] ≤ 10 5 \texttt{-10}^\texttt{5} \le \texttt{matrix[i][j]} \le \texttt{10}^\texttt{5} -105≤matrix[i][j]≤105
- 0 ≤ row1 ≤ row2 < m \texttt{0} \le \texttt{row1} \le \texttt{row2} < \texttt{m} 0≤row1≤row2<m
- 0 ≤ col1 ≤ col2 < n \texttt{0} \le \texttt{col1} \le \texttt{col2} < \texttt{n} 0≤col1≤col2<n
- 最多调用 10 4 \texttt{10}^\texttt{4} 104 次 sumRegion \texttt{sumRegion} sumRegion 方法
前言
这道题是「区域和检索 - 数组不可变」的进阶,要求计算子矩阵的元素和。
这道题可以复用「区域和检索 - 数组不可变」的做法,计算矩阵每一行的一维前缀和,计算子矩阵的元素和时遍历子矩阵的每一行,但是该做法的每次查询的时间复杂度和查询范围的行数有关,无法实现 O ( 1 ) O(1) O(1) 时间的查询。使用二维前缀和,则可以实现 O ( 1 ) O(1) O(1) 时间的查询。
解法
思路和算法
为了实现 O ( 1 ) O(1) O(1) 时间的查询,需要预计算整个矩阵的前缀和矩阵。
创建 ( m + 1 ) × ( n + 1 ) (m + 1) \times (n + 1) (m+1)×(n+1) 的前缀和矩阵 prefixSums \textit{prefixSums} prefixSums,对于 0 ≤ i ≤ m 0 \le i \le m 0≤i≤m 和 0 ≤ j ≤ n 0 \le j \le n 0≤j≤n, prefixSums [ i ] [ j ] \textit{prefixSums}[i][j] prefixSums[i][j] 表示 matrix [ i ] \textit{matrix}[i] matrix[i] 的行数为 i i i、列数为 j j j 的前缀和,即行下标范围 [ 0 , i − 1 ] [0, i - 1] [0,i−1]、列下标范围 [ 0 , j − 1 ] [0, j - 1] [0,j−1] 中的所有元素之和:
prefixSums [ i ] [ j ] = ∑ 0 ≤ p < i , 0 ≤ q < j matrix [ p ] [ q ] \textit{prefixSums}[i][j] = \sum\limits_{0 \le p < i, 0 \le q < j} \textit{matrix}[p][q] prefixSums[i][j]=0≤p<i,0≤q<j∑matrix[p][q]
特别地,当 i i i 和 j j j 中至少有一个值等于 0 0 0 时, prefixSums [ i ] [ j ] = 0 \textit{prefixSums}[i][j] = 0 prefixSums[i][j]=0。
对于 0 ≤ i < m 0 \le i < m 0≤i<m 和 0 ≤ j < n 0 \le j < n 0≤j<n, prefixSums [ i + 1 ] [ j + 1 ] \textit{prefixSums}[i + 1][j + 1] prefixSums[i+1][j+1] 的值计算如下:
prefixSums [ i + 1 ] [ j + 1 ] = prefixSums [ i ] [ j + 1 ] + prefixSums [ i + 1 ] [ j ] − prefixSums [ i ] [ j ] + matrix [ i ] [ j ] \begin{aligned} &\textit{prefixSums}[i + 1][j + 1] \\ = &\textit{prefixSums}[i][j + 1] \\ &+ \textit{prefixSums}[i + 1][j] \\ &- \textit{prefixSums}[i][j] \\ &+ \textit{matrix}[i][j] \end{aligned} =prefixSums[i+1][j+1]prefixSums[i][j+1]+prefixSums[i+1][j]−prefixSums[i][j]+matrix[i][j]
可以结合下图理解前缀和矩阵的计算方式。

图中的四个区域对应的原始矩阵的行下标范围和列下标范围如下。
-
A 区域的行下标范围是 [ 0 , i − 1 ] [0, i - 1] [0,i−1],列下标范围是 [ 0 , j − 1 ] [0, j - 1] [0,j−1]。
-
B 区域的行下标范围是 [ 0 , i − 1 ] [0, i - 1] [0,i−1],列下标是 j j j。
-
C 区域的行下标是 i i i,列下标范围是 [ 0 , j − 1 ] [0, j - 1] [0,j−1]。
-
D 区域的行下标是 i i i,列下标是 j j j。
前缀和 prefixSums [ i + 1 ] [ j + 1 ] \textit{prefixSums}[i + 1][j + 1] prefixSums[i+1][j+1] 应将 A、B、C、D 四个区域各计算一次。计算前缀和的各项中, prefixSums [ i ] [ j + 1 ] \textit{prefixSums}[i][j + 1] prefixSums[i][j+1] 为 A 区域和 B 区域, prefixSums [ i + 1 ] [ j ] \textit{prefixSums}[i + 1][j] prefixSums[i+1][j] 为 A 区域和 C 区域, prefixSums [ i ] [ j ] \textit{prefixSums}[i][j] prefixSums[i][j] 为 A 区域, matrix [ i ] [ j ] \textit{matrix}[i][j] matrix[i][j] 为 D 区域,因此可以通过上述方法计算前缀和矩阵。
得到前缀和矩阵 prefixSums \textit{prefixSums} prefixSums 之后,对于 0 ≤ row 1 ≤ row 2 < m 0 \le \textit{row}_1 \le \textit{row}_2 < m 0≤row1≤row2<m 和 0 ≤ col 1 ≤ col 2 < n 0 \le \textit{col}_1 \le \textit{col}_2 < n 0≤col1≤col2<n,以 ( row 1 , col 1 ) (\textit{row}_1, \textit{col}_1) (row1,col1) 为左上角、 ( row 2 , col 2 ) (\textit{row}_2, \textit{col}_2) (row2,col2) 为右下角的子矩阵的元素和可以通过前缀和矩阵得到:
sumRegion ( row 1 , col 1 , row 2 , col 2 ) = prefixSums [ row 2 + 1 ] [ col 2 + 1 ] − prefixSums [ row 1 ] [ col 2 + 1 ] − prefixSums [ row 2 + 1 ] [ col 1 ] + prefixSums [ row 1 ] [ col 1 ] \begin{aligned} &\textit{sumRegion}(\textit{row}_1, \textit{col}_1, \textit{row}_2, \textit{col}_2) \\ = &\textit{prefixSums}[\textit{row}_2 + 1][\textit{col}_2 + 1] \\ &- \textit{prefixSums}[\textit{row}_1][\textit{col}_2 + 1] \\ &- \textit{prefixSums}[\textit{row}_2 + 1][\textit{col}_1] \\ &+ \textit{prefixSums}[\textit{row}_1][\textit{col}_1] \end{aligned} =sumRegion(row1,col1,row2,col2)prefixSums[row2+1][col2+1]−prefixSums[row1][col2+1]−prefixSums[row2+1][col1]+prefixSums[row1][col1]
可以结合下图理解子矩阵元素和的计算方式。

图中的四个区域对应的原始矩阵的行下标范围和列下标范围如下。
-
A 区域的行下标范围是 [ 0 , row 1 − 1 ] [0, \textit{row}_1 - 1] [0,row1−1],列下标范围是 [ 0 , col 1 − 1 ] [0, \textit{col}_1 - 1] [0,col1−1]。
-
B 区域的行下标范围是 [ 0 , row 1 − 1 ] [0, \textit{row}_1 - 1] [0,row1−1],列下标范围是 [ col 1 , col 2 ] [\textit{col}_1, \textit{col}_2] [col1,col2]。
-
C 区域的行下标范围是 [ row 1 , row 2 ] [\textit{row}_1, \textit{row}_2] [row1,row2],列下标范围是 [ 0 , col 1 − 1 ] [0, \textit{col}_1 - 1] [0,col1−1]。
-
D 区域的行下标范围是 [ row 1 , row 2 ] [\textit{row}_1, \textit{row}_2] [row1,row2],列下标范围是 [ col 1 , col 2 ] [\textit{col}_1, \textit{col}_2] [col1,col2]。
需要计算元素和的子矩阵是 D 区域。计算子矩阵元素和的各项中, prefixSums [ row 2 + 1 ] [ col 2 + 1 ] \textit{prefixSums}[\textit{row}_2 + 1][\textit{col}_2 + 1] prefixSums[row2+1][col2+1] 为 A、B、C、D 四个区域, prefixSums [ row 1 ] [ col 2 + 1 ] \textit{prefixSums}[\textit{row}_1][\textit{col}_2 + 1] prefixSums[row1][col2+1] 为 A 区域和 B 区域, prefixSums [ row 2 + 1 ] [ col 1 ] \textit{prefixSums}[\textit{row}_2 + 1][\textit{col}_1] prefixSums[row2+1][col1] 为 A 区域和 C 区域, prefixSums [ row 1 ] [ col 1 ] \textit{prefixSums}[\textit{row}_1][\textit{col}_1] prefixSums[row1][col1] 为 A 区域,因此可以通过上述方法计算子矩阵元素和。
代码
class NumMatrix {int[][] prefixSums;public NumMatrix(int[][] matrix) {int m = matrix.length, n = matrix[0].length;prefixSums = new int[m + 1][n + 1];for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {prefixSums[i + 1][j + 1] = prefixSums[i][j + 1] + prefixSums[i + 1][j] - prefixSums[i][j] + matrix[i][j];}}}public int sumRegion(int row1, int col1, int row2, int col2) {return prefixSums[row2 + 1][col2 + 1] - prefixSums[row1][col2 + 1] - prefixSums[row2 + 1][col1] + prefixSums[row1][col1];}
}
复杂度分析
-
时间复杂度:构造方法的时间复杂度是 O ( m × n ) O(m \times n) O(m×n), sumRegion \textit{sumRegion} sumRegion 操作的时间复杂度是 O ( 1 ) O(1) O(1),其中 m m m 和 n n n 分别是矩阵 matrix \textit{matrix} matrix 的行数和列数。构造方法需要创建 ( m + 1 ) × ( n + 1 ) (m + 1) \times (n + 1) (m+1)×(n+1) 的前缀和矩阵并计算每个元素的前缀和,每次 sumRegion \textit{sumRegion} sumRegion 操作计算子矩阵的元素和的时间是 O ( 1 ) O(1) O(1)。
-
空间复杂度: O ( m × n ) O(m \times n) O(m×n),其中 m m m 和 n n n 分别是矩阵 matrix \textit{matrix} matrix 的行数和列数。需要创建 ( m + 1 ) × ( n + 1 ) (m + 1) \times (n + 1) (m+1)×(n+1) 的前缀和矩阵。