C++二叉树常见OJ题分析-海口c网

OJ（一）：根据二叉树创建字符串

606. 根据二叉树创建字符串 - 力扣（LeetCode）

1.（ps:接下来的解答来自LeetCode的官方解释：这里只是为了让以后复习便利而已。）

如果当前节点有两个孩子，那我们在递归时，需要在两个孩子的结果外都加上一层括号；

如果当前节点没有孩子，那我们不需要在节点后面加上任何括号；

如果当前节点只有左孩子，那我们在递归时，只需要在左孩子的结果外加上一层括号，而不需要给右孩子加上任何括号；
如果当前节点只有右孩子，那我们在递归时，需要先加上一层空的括号 ‘()’ 表示左孩子为空，再对右孩子进行递归，并在结果外加上一层括号。

class Solution {
public:string tree2str(TreeNode* root) {if(root==nullptr)return "";string str=to_string(root->val);if(root->left ||root->right){str+="(";str+=tree2str(root->left);str+=")";}if(root->right){str+="(";str+=tree2str(root->right);str+=")";}return str;}
};

OJ（二）：二叉树的最近公共祖先

情况一：它们其中一个是根节点，就直接返回根。

情况二：

根据上面我们图知:如果一个在左树，一个在右树，那么当前根就是它们最近的公共祖先。

解释：

1.我们要写一个find函数，用来找它们是符合哪种情况：即找它们是在那支树里

若一个在左树，一个在右树，直接返回它们的当前根

若两个都在当前树的同一支树，则继续去递归，进去下一个更近的树。

2.所以我们可以定义四个变量：即代码中的pInLeft,pInRight,qInLeft,qInRight，返回类型是bool

其中，按照上面的变量名，到下面，你就会很清晰地看到它的优势。
class Solution {
public:bool Find(TreeNode*tree,TreeNode* x){if(tree==nullptr)return false;return tree==x||Find(tree->left,x)||Find(tree->right,x);}TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {if(root==nullptr)return nullptr;if(root==p||root==q)return root;bool pInLeft,pInRight,qInLeft,qInRight;pInLeft=Find(root->left,p);//这里就直接逻辑取反即可，因为p不是左就是右pInRight=!pInLeft;qInLeft=Find(root->left,q);//这里就直接逻辑取反即可，因为q不是左就是右qInRight=!qInLeft;//如果都在左边if(pInLeft &&qInLeft){return lowestCommonAncestor(root->left,p,q);}//都在右边else if(pInRight &&qInRight){return lowestCommonAncestor(root->right,p,q);}return root;}
};

法二：利用栈去完成。

1.建立两个栈，分别把它们经过遍历的值都push进去各自的栈中，知道找到它们的值为止。

接着，如果它们栈的长度不一样的话，先pop掉长的那个栈，令它们的长度相等，再去比较

比较时，如果它们两个的栈顶值不一样时，就pop掉，反之，它们两个栈顶的值相等时，即找到了它们的最近公共祖先了。

class Solution {
public://找路径的函数bool Findpath(TreeNode*root,TreeNode*x,stack<TreeNode*>& path){if(root==nullptr)return false;path.push(root);if(root==x){return true;}//如果不为空，说明找到了if(Findpath(root->left,x,path)){return true;}  if(Findpath(root->right,x,path)){return true;}//如果到最后都找不到，所以没有，就需要pop掉一开始的值path.pop();return false;}TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {stack<TreeNode*>ppath,qpath;Findpath(root,p,ppath);Findpath(root,q,qpath);while(ppath.size()>qpath.size()){ppath.pop();}while(ppath.size()<qpath.size()){qpath.pop();}while(ppath.top()!=qpath.top()){qpath.pop();ppath.pop();}return ppath.top();}
};

OJ（三）：二叉树的分层遍历

102. 二叉树的层序遍历 - 力扣（LeetCode）

层序遍历：一层一层地遍历

1.这里使用到了队列来借助完成

2.开始时先入它的根，接着进入循环（条件是：队列不为空）

记录下队列的头结点，再从队列里删去。接着再从已经记录的头节点，去看它的左子树和右子树为不为空，不为空的话，就push进去队列（记得按照左->的顺序入队列）

把每一层的值放进去vector<int>后，再统一把这一层的值push进去ret中。
class Solution {
public:vector<vector<int>> levelOrder(TreeNode* root) {vector<vector<int>> ret;//注意这里放的是它的结点，所以类型不要弄成int了queue<TreeNode*> q;if(root)q.push(root);while(!q.empty()){vector<int >ans;int size=q.size();for(int i=1;i<=size;i++){//这里也是注意是结点，而不是intTreeNode*cur=q.front();q.pop();ans.push_back(cur->val);if(cur->left){q.push(cur->left);}if(cur->right){q.push(cur->right);}} ret.push_back(ans);}return ret;}
};

OJ（四）：二叉树的层序遍历2

107. 二叉树的层序遍历 II - 力扣（LeetCode）

这里跟上面的一样的，只是这道题的最后需要你逆置一下即可

多了一行与上一题：reverse(vv.begin(),vv.end());

class Solution {
public:vector<vector<int>> levelOrderBottom(TreeNode* root) {vector<vector<int>> vv;queue<TreeNode*>q;if(root)q.push(root);while(!q.empty()){vector<int> v;int size=q.size();for(int i=0;i<size;i++){TreeNode*cur=q.front();q.pop();v.push_back(cur->val);if(cur->left)q.push(cur->left);if(cur->right)q.push(cur->right);}vv.push_back(v);}reverse(vv.begin(),vv.end());return vv;}
};

OJ(四)：二叉搜索树与双向链表

二叉搜索树与双向链表_牛客题霸_牛客网

left:中序上一个

right:中序下一个

画递归图：就可以更加直观了，这里就并不画了。
class Solution {
public:void Inorder(TreeNode*cur,TreeNode*&prev){if(cur==nullptr)return;Inorder(cur->left, prev);cur->left=prev;if(prev)prev->right=cur;prev=cur;Inorder(cur->right, prev);}TreeNode* Convert(TreeNode* pRootOfTree) {TreeNode*prev=nullptr;Inorder(pRootOfTree,prev);TreeNode*head=pRootOfTree;while(head &&head->left){head=head->left;}return head;}
};

OJ(五)：从前序与中序遍历序列构造二叉树

105. 从前序与中序遍历序列构造二叉树 - 力扣（LeetCode）

注意：previ加&

class Solution {
public:TreeNode* _buildTree(vector<int>& preorder, vector<int>& inorder,int& previ,int inbegin,int inend){if(inbegin>inend)return nullptr;TreeNode*root=new TreeNode(preorder[previ]);int rooti=inbegin;//找根在中序的那个位置while(rooti<inend){if(preorder[previ]==inorder[rooti])break;rooti++;}previ++;root->left=_buildTree(preorder,inorder,previ,inbegin,rooti-1);root->right=_buildTree(preorder,inorder,previ,rooti+1,inend);return root;}TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {int i=0;TreeNode*root=_buildTree(preorder,inorder,i,0,inorder.size()-1);return root;}
};

OJ（六）：从中序与后序遍历序列构造二叉树

106. 从中序与后序遍历序列构造二叉树 - 力扣（LeetCode）

这道题跟上面那道题差不多相似的。

因为我们想想：

后序：左右根前序：根左右

那么，它们的区别不过只是，后序的根在最后，前序的根在开始而已。并且后序的顺序是从右子树到左子树，前序的顺序是从左子树到右子树。
class Solution {
public:TreeNode* _buildTree(vector<int>& inorder, vector<int>& postorder,int& posti,int inbegin,int inend){if(inbegin>inend)return nullptr;TreeNode*root=new TreeNode(postorder[posti]);int rooti=inbegin;while(rooti<inend){if(postorder[posti]==inorder[rooti])break;rooti++;}posti--;//先右再左root->right=_buildTree(inorder,postorder,posti,rooti+1,inend);root->left=_buildTree(inorder,postorder,posti,inbegin,rooti-1);return root;} TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {//最后一个下标int i=postorder.size()-1;TreeNode*root=_buildTree(inorder,postorder,i,0,inorder.size()-1);return root;}
};

OJ(七)：二叉树的前序遍历（非递归）

1.利用栈来完成：

class Solution {
public:vector<int> preorderTraversal(TreeNode* root) {stack<TreeNode*>st;vector<int> v;TreeNode*cur=root;while(cur || !st.empty()){while(cur){v.push_back(cur->val);st.push(cur);cur=cur->left;}TreeNode*front=st.top();st.pop();cur=front->right;}return v;}
};

OJ(八)：二叉树的中序遍历（非递归）

94. 二叉树的中序遍历 - 力扣（LeetCode）

这个跟前序差不多很相似：

class Solution {
public:vector<int> inorderTraversal(TreeNode* root) {stack<TreeNode*>st;vector<int> v;TreeNode*cur=root;while(cur||!st.empty()){while(cur){st.push(cur);cur=cur->left;}TreeNode*front=st.top();st.pop();v.push_back(front->val);cur=front->right;}return v;}
};

OJ(九)：二叉树的后序遍历（非递归）

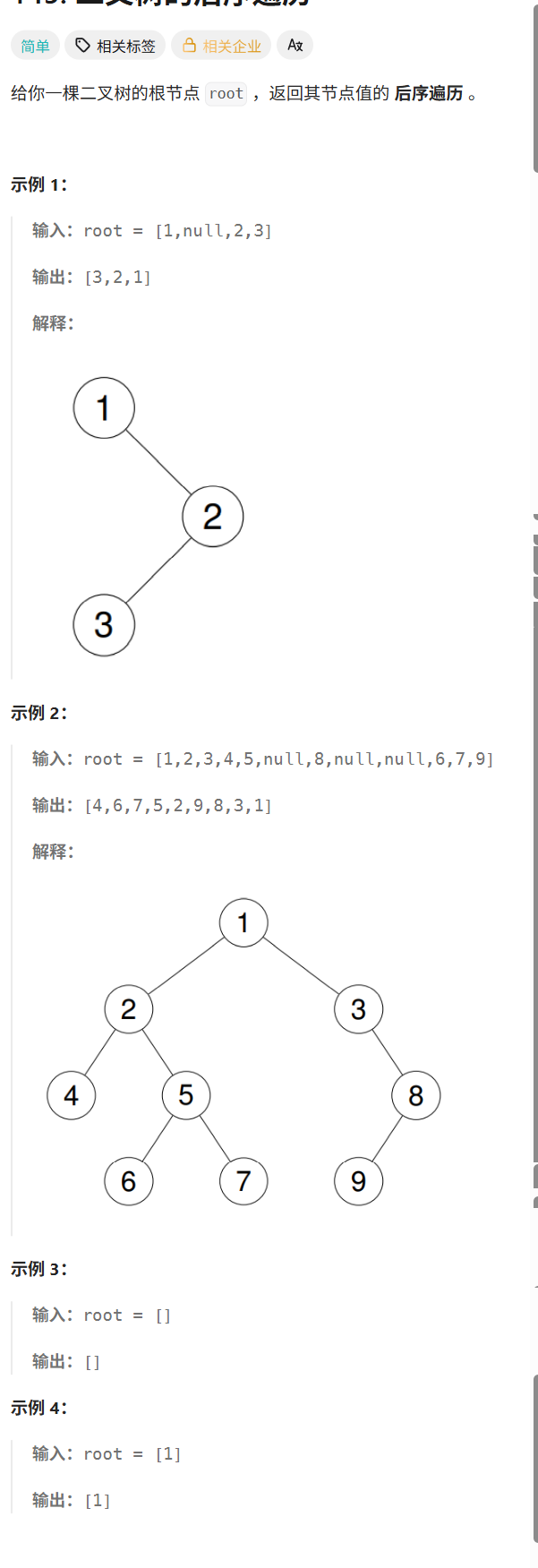
145. 二叉树的后序遍历 - 力扣（LeetCode）

这里与前面两道有所差异：

这里后序遍历时：使用到了prev来记录前一个结点

class Solution {
public:vector<int> postorderTraversal(TreeNode* root) {stack<TreeNode*>st;vector<int>v;TreeNode*cur=root;TreeNode*prev=nullptr;while(cur ||!st.empty()){//左树while(cur){st.push(cur);cur=cur->left;}TreeNode*front=st.top();//因为上面循环中已经知道了cur为空了，即说明左子树已经空了，//左右只需要看它的右子树是否空，如果为空，所以这个是最左边的数了，//就可以进行插入v了，而且第二个是防止它本身就在右子树的，已经遍历完的情况if(front->right==nullptr ||front->right==prev){v.push_back(front->val);prev=front;st.pop();}elsecur=front->right;}return v;}
};

好了，关于二叉树的OJ题分析就到此结束了，希望大家都有所收获！