教学感悟
以前在传授数列时只是机械的要求学生记住常见的数列,至于“哪些才算是常见的数列?这些数列是怎么来的”,心里比较糊涂,在有一次的教学中,偶然回忆起:函数教学时教材要求掌握一些常见的函数,对比这些数列和函数,心里豁然开朗。有图为证:
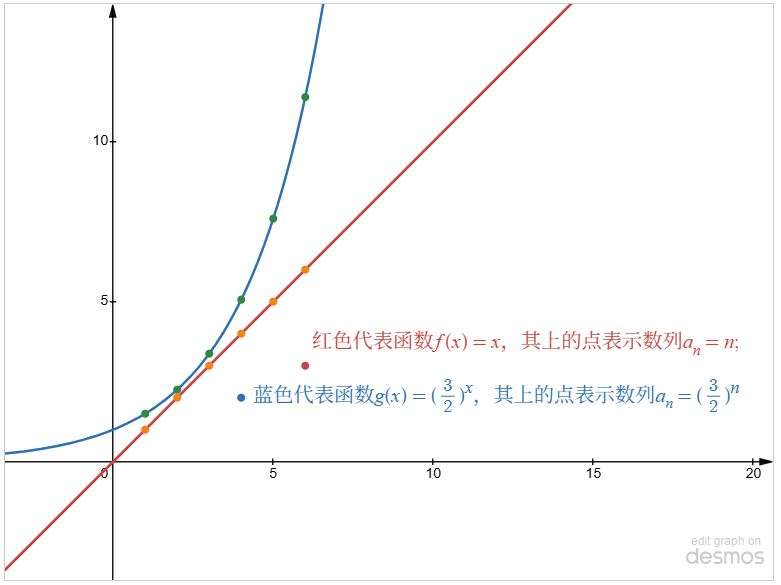
比如说特殊的幂函数: y = x y=x y=x, y = x 2 y=x^2 y=x2, y = 1 x y=\cfrac{1}{x} y=x1;
特殊的指数函数: y = 2 x y=2^x y=2x, y = 3 x y=3^x y=3x, y = 10 x y=10^x y=10x, ⋯ \cdots ⋯,
这些函数都是函数教学中比较常见和重要的函数,使用的频度比较高,那么考查以下基于这些函数的数列就是自然而然的事情了。
依托函数
- 基于函数 y = x 2 y=x^2 y=x2的数列,比如说:
数列 1 \;1 1, 4 4 4, 9 9 9, 16 16 16, 25 25 25, ⋯ \cdots ⋯,归纳总结得到,其通项公式是 a n = n 2 a_n=n^2 an=n2;
数列 0 \;0 0, 3 3 3, 8 8 8, 15 15 15, 24 24 24, ⋯ \cdots ⋯,归纳总结得到,其通项公式是 a n = n 2 − 1 a_n=n^2-1 an=n2−1;
数列 2 \;2 2, 5 5 5, 10 10 10, 17 17 17, 26 26 26, ⋯ \cdots ⋯,归纳总结得到,其通项公式是 a n = n 2 + 1 a_n=n^2+1 an=n2+1;
数列 2 \;2 2, 6 6 6, 12 12 12, 20 20 20, 30 30 30, ⋯ \cdots ⋯,归纳总结得到,其通项公式是 a n = n ( n + 1 ) a_n=n(n+1) an=n(n+1);
数列 0 \;0 0, 2 2 2, 6 6 6, 12 12 12, 20 20 20, ⋯ \cdots ⋯,归纳总结得到,其通项公式是 a n = n ( n − 1 ) a_n=n(n-1) an=n(n−1);
数列 3 \;3 3, 15 15 15, 35 35 35, 63 63 63, 99 99 99, ⋯ \cdots ⋯,归纳总结得到,其通项公式是 a n = ( 2 n − 1 ) ( 2 n + 1 ) a_n=(2n-1)(2n+1) an=(2n−1)(2n+1);
数列 8 \;8 8, 24 24 24, 48 48 48, 80 80 80, 120 120 120, ⋯ \cdots ⋯,归纳总结得到,其通项公式是 a n = 2 n ( 2 n + 2 ) a_n=2n(2n+2) an=2n(2n+2);
- 基于函数 y = 1 x y=\cfrac{1}{x} y=x1的数列,比如说:
数列 1 \;1 1, 1 2 \cfrac{1}{2} 21, 1 3 \cfrac{1}{3} 31, 1 4 \cfrac{1}{4} 41, 1 5 \cfrac{1}{5} 51, ⋯ \cdots ⋯,归纳总结得到,其通项公式是 a n = 1 n a_n=\cfrac{1}{n} an=n1;
数列 1 2 \cfrac{1}{2} 21, 1 6 \cfrac{1}{6} 61, 1 12 \cfrac{1}{12} 121, 1 20 \cfrac{1}{20} 201, 1 30 \cfrac{1}{30} 301, ⋯ \cdots ⋯,归纳总结得到,其通项公式是 a n = 1 n ( n + 1 ) a_n=\cfrac{1}{n(n+1)} an=n(n+1)1
数列 1 \;1 1, 1 3 \cfrac{1}{3} 31, 1 7 \cfrac{1}{7} 71, 1 15 \cfrac{1}{15} 151, 1 31 \cfrac{1}{31} 311, ⋯ \cdots ⋯,其通项公式是 a n = 1 2 n − 1 a_n=\cfrac{1}{2^n-1} an=2n−11;
数列 1 \;1 1, 1 4 \cfrac{1}{4} 41, 1 9 \cfrac{1}{9} 91, 1 16 \cfrac{1}{16} 161, 1 25 \cfrac{1}{25} 251, ⋯ \cdots ⋯,其通项公式是 a n = 1 n 2 a_n=\cfrac{1}{n^2} an=n21;
- 基于函数 y = 2 x y=2^x y=2x的数列,比如说
数列 1 \;1 1, 2 2 2, 4 4 4, 8 8 8, 16 16 16, ⋯ \cdots ⋯,其通项公式是 a n = 2 n − 1 a_n=2^{n-1} an=2n−1;
数列 0 \;0 0, 1 1 1, 3 3 3, 7 7 7, 15 15 15, ⋯ \cdots ⋯,其通项公式是 a n = 2 n − 1 − 1 a_n=2^{n-1}-1 an=2n−1−1;
- 基于函数 y = 3 x y=3^x y=3x的数列,比如说
数列 1 \;1 1, 3 3 3, 9 9 9, 27 27 27, 81 81 81, ⋯ \cdots ⋯,其通项公式是 a n = 3 n − 1 a_n=3^{n-1} an=3n−1;
数列 2 \;2 2, 4 4 4, 10 10 10, 28 28 28, 82 82 82, ⋯ \cdots ⋯,其通项公式是 a n = 3 n − 1 + 1 a_n=3^{n-1}+1 an=3n−1+1;
- 基于函数 y = 10 x y=10^x y=10x的数列,比如说
数列 0.1 \;0.1 0.1, 0.01 0.01 0.01, 0.001 0.001 0.001, 0.0001 0.0001 0.0001, ⋯ \cdots ⋯,其通项公式是 a n = ( 1 10 ) n a_n=(\cfrac{1}{10})^n an=(101)n;
数列 9 \;9 9, 99 99 99, 999 999 999, 9999 9999 9999, 99999 99999 99999, ⋯ \cdots ⋯,其通项公式是 a n = 10 n − 1 a_n=10^n-1 an=10n−1;
数列 5 \;5 5, 55 55 55, 555 555 555, 5555 5555 5555, 55555 55555 55555, ⋯ \cdots ⋯,其通项公式是 a n = 5 9 ( 10 n − 1 ) a_n=\cfrac{5}{9}(10^n-1) an=95(10n−1);
数列 0.9 \;0.9 0.9, 0.99 0.99 0.99, 0.999 0.999 0.999, 0.9999 0.9999 0.9999, ⋯ \cdots ⋯,其通项公式是 a n = 1 − ( 1 10 ) n a_n=1-(\cfrac{1}{10})^n an=1−(101)n;
- 符号数列或者符号因子数列 { ( − 1 ) k } \{(-1)^k\} {(−1)k}或 { ( − 1 ) k + 1 } \{(-1)^{k+1}\} {(−1)k+1}
( − 1 ) k (-1)^k (−1)k: − 1 -1 −1, 1 1 1, − 1 -1 −1, 1 1 1, − 1 -1 −1, 1 1 1, ⋯ \cdots ⋯,奇数项为负,偶数项为正;
( − 1 ) k + 1 (-1)^{k+1} (−1)k+1: 1 1 1, − 1 -1 −1, 1 1 1, − 1 -1 −1, 1 1 1, − 1 -1 −1, ⋯ \cdots ⋯,奇数项为正,偶数项为负;
有了以上的感悟和理解,我们再来看教材,也终于能理解编写者的良苦用意了。
小试牛刀
- 给定数列的前有限项,求数列 { a n } \{a_n\} {an}的通项公式
考查方法:常以选择填空题形式考查;主要考查观察归纳法,熟练记忆常见数列的通项公式,然后组合即可突破此类问题。
No.1、数列 15 2 \cfrac{15}{2} 215, − 24 5 -\cfrac{24}{5} −524, 35 10 \cfrac{35}{10} 1035, − 48 17 -\cfrac{48}{17} −1748, 63 26 \cfrac{63}{26} 2663, ⋯ \cdots ⋯的一个通项公式为 a n a_n an=____________;
提示: a n = ( − 1 ) n + 1 ⋅ ( n + 3 ) 2 − 1 n 2 + 1 a_n=(-1)^{n+1}\cdot \cfrac{(n+3)^2-1}{n^2+1} an=(−1)n+1⋅n2+1(n+3)2−1;
No.2、数列 1 2 \cfrac{1}{2} 21, 1 4 \cfrac{1}{4} 41, − 5 8 -\cfrac{5}{8} −85, 13 16 \cfrac{13}{16} 1613, − 29 32 -\cfrac{29}{32} −3229, 61 64 \cfrac{61}{64} 6461, ⋯ \cdots ⋯,的一个通项公式为 a n a_n an=____________;
提示:变形为 − 2 1 − 3 2 1 -\cfrac{2^1-3}{2^1} −2121−3, 2 2 − 3 2 2 \cfrac{2^2-3}{2^2} 2222−3, − 2 3 − 3 2 3 -\cfrac{2^3-3}{2^3} −2323−3, 2 4 − 3 2 4 \cfrac{2^4-3}{2^4} 2424−3, − 2 5 − 3 2 5 -\cfrac{2^5-3}{2^5} −2525−3, 2 6 − 3 2 6 \cfrac{2^6-3}{2^6} 2626−3,
故 a n = ( − 1 ) n 2 n − 3 2 n a_n=(-1)^n\cfrac{2^n-3}{2^n} an=(−1)n2n2n−3;
No.3、已知数列的前 4 4 4项为 2 2 2, 0 0 0, 2 2 2, 0 0 0,则依次归纳该数列的通项公式不可能是【】
A . a n = ( − 1 ) n − 1 + 1 A.a_n=(-1)^{n-1}+1 A.an=(−1)n−1+1
分析:选 C C C,由前有限项归纳通项公式,结果可能不唯一;
No.4、数列 1 1 1, 3 3 3, 6 6 6, 10 10 10, 15 15 15, ⋯ \cdots ⋯的一个通项公式为【 \quad 】
A . a n = n 2 − ( n − 1 ) A.a_n=n^2-(n-1) A.an=n2−(n−1)
分析:
1 = 1 1=1 1=1;
3 = 1 + 2 3=1+2 3=1+2;
6 = 1 + 2 + 3 6=1+2+3 6=1+2+3;
10 = 1 + 2 + 3 + 4 10=1+2+3+4 10=1+2+3+4;
⋯ , ⋯ \cdots,\cdots ⋯,⋯
所以第 n n n项为 1 + 2 + 3 + ⋯ + n = n ( n + 1 ) 2 1+2+3+\cdots+n=\cfrac{n(n+1)}{2} 1+2+3+⋯+n=2n(n+1),故选 C C C.
No.5、【2021届高三文科二轮资料用题】对大于 1 1 1 的自然数的三次幕可以分解成几个奇数的和,比如 2 3 = 3 + 5 2^3=3+5 23=3+5, 3 3 = 7 + 9 + 11 3^{3}=7+9+11 33=7+9+11, 4 3 = 13 + 15 + 17 + 19 4^{3}=13+15+17+19 43=13+15+17+19, ⋯ \cdots ⋯, 以此规律,则 45 3 45^{3} 453 的分解和式中一定不含有【 \quad 】
A .2069 A.2069 A.2069 B .2039 B.2039 B.2039 C .2009 C.2009 C.2009 D .1979 D.1979 D.1979
解析:观察总结可知, n 3 n^3 n3 的分解式有 n n n 个奇数的和,而
2 3 2^3 23 的展开式中的第一项为 3 = 1 × 2 + 1 3=1\times 2+1 3=1×2+1;
3 3 3^3 33 的展开式中的第一项为 7 = 2 × 3 + 1 7=2\times 3+1 7=2×3+1;
4 3 4^3 43 的展开式中的第一项为 13 = 3 × 4 + 1 13=3\times 4+1 13=3×4+1;
5 3 5^3 53 的展开式中的第一项为 21 = 4 × 5 + 1 21=4\times 5+1 21=4×5+1;
故归纳总结可知, 45 3 45^3 453的展开式中的第一项必然为 44 × 45 + 1 = 1981 44\times 45+1=1981 44×45+1=1981,
故 45 3 45^{3} 453 的分解和式中一定不含有 1979 1979 1979,故选 D D D.