「动态规划::状压DP」网格图递推 / AcWing 292|327（C++）-海口c网

概述

相邻行递推

思路

算法过程

优化方案

空间优化

返回值优化

Code

复杂度

相邻两行递推

思路

算法过程

Code

复杂度

特殊优化：编译期计算

总结

概述

如果我们有一张地图，要求是在符合某类条件的前提在地图上放置最优解，该怎么计算？

这也属于状压dp的应用之一。

相邻行递推

AcWing 237：

农夫约翰的土地由 M×N 个小方格组成，现在他要在土地里种植玉米。

非常遗憾，部分土地是不育的，无法种植。

而且，相邻的土地不能同时种植玉米，也就是说种植玉米的所有方格之间都不会有公共边缘。

现在给定土地的大小，请你求出共有多少种种植方法。

土地上什么都不种也算一种方法。

输入格式

第 1 行包含两个整数 M 和 N。

第 2..M+1 行：每行包含 N 个整数 0 或 1，用来描述整个土地的状况，1 表示该块土地肥沃，0 表示该块土地不育。

输出格式

输出总种植方 1e8 取模后的值。

数据范围

1≤M,N≤12

输入样例：
2 3
1 1 1
0 1 0
输出样例：
9

思路

之所以可以进行状压dp是因为列的数量较小，我们可以把一行压缩成一个整数。

也就是说我们有地图状态 g[i] = (10011) $^{_{2}}$ ，意味着第 i 行的第0、1、4列可以种植。

我们发现需要两个状态：当前行序号和当前行内种植的情况。

定义 dp[i][k]，表示[0, i] 行内且第 i 行状态为 k 的种植方案数，例如：

若 k = (10001) $^{_{2}}$ ，意味着第 i 行的种植了第0、4列。

那么dp[i][k]可以从什么转移来呢？我们发现有以下约束：

k 要服从地图的约束，也就是第 i 行的合法 k 仅能是 g[i] 的子集。
k 内不含有相邻1，也就是行内需要合法。
第 i 行 k 也不能与 i - 1 行 k 不含有相邻1，也就是行间需要合法。

基于此，我们可以得知转移方程： dp[i][k] = $\sum$ dp[i - 1][t]。

其中，k、t 都行内合法且符合地图约束，且 k 与 t 行间兼容。

初始条件下，dp[0][服从地图0行的k] = 1。

算法过程

可以预处理出合法的 k。

行内合法的条件是： (k & (k >> 1) == 0。什么意思呢？k 的二进制位右移1位，与原来的 k 作与运算，就是试图让相邻的1重叠在一起，若真的有相邻的1，那么与运算结果必不为0。

为什么不用考虑左移呢？因为对于相邻的11，右1左移和左1右移是一样的。

如果你纠结于右移的溢出位的话，可以将二进制串前后补上无限长的0，再感受一下。

符合地图约束的k的条件：(k | g[i]) == g[i]。意味着k是g[i]的子集。
行间合法的条件是：(k1 & k2) == 0。意味着二者无重合的1，作为上下行时，就没有相邻的1。

那代码大概是这样的：

int solve(){for (int k = 0; k <= mx; k++)if (!(k & (k >> 1)))st.push_back(k);for (int k : st)if ((k | g[0]) == g[0])dp[0][k] = 1;for (int i = 1; i < m; i++)for (int k : st) if((k | g[i]) == g[i])for (int pre_k : st) if (!(k & pre_k) && (pre_k | g[i - 1]) == g[i - 1])dp[i][k] = (dp[i][k] + dp[i - 1][pre_k]) % MOD;int ans = 0;for (int k : st)ans = (ans + dp[m - 1][k]) % MOD;return ans;
}

优化方案

空间优化

注意到dp[i]总是来自上一行dp[i - 1]，所以可以做一层空间优化。

仅使用两行储存dp，怎么区分哪行是上一行，哪行是这一行呢？

注意到枚举 i 时， i 的奇偶性持续发生变化，我们用 i & 1 作索引，dp[i & 1]储存第 i 行，dp[(i - 1) & 1] 就是上一行，当开始计算dp[i & 1][k]时，要先置 0 ，清除上上行的状态。

返回值优化

在最后，我们选择 i 多枚举1行，即计算到 i == m，此时答案就储存在 dp[m & 1][0]中，即 m 行，那个不存在的行，放置情况是0时即全空，这时的总状态。

Code

#include <bits/stdc++.h>
using namespace std;
constexpr int N = 13, MOD = 1e8;
int m, n, mx;
int g[N], dp[2][1 << N];
vector<int> st;
int solve(){for (int k = 0; k <= mx; k++)if (!(k & (k >> 1)))st.push_back(k);for (int k : st)if ((k | g[0]) == g[0])dp[0][k] = 1;for (int i = 1; i <= m; i++)for (int k : st) if((k | g[i]) == g[i]) {dp[i & 1][k] = 0;for (int pre_k : st) if (!(k & pre_k) && (pre_k | g[i - 1]) == g[i - 1])dp[i & 1][k] = (dp[i & 1][k] + dp[(i - 1) & 1][pre_k]) % MOD;}return dp[m & 1][0];
}
int main(){cin >> m >> n;  mx = (1 << n) - 1;for (int i = 0; i < m; i++)for (int j = 0; j < n; j++) {int x; cin >> x;g[i] |= x << j;}cout << solve();return 0;
}

复杂度

时间复杂度: O( + $m(\frac{1 + \sqrt{5}}{2}) ^{n}$ )

空间复杂度: O( $2^{n}$ )

n：列数

m：行数

复杂度分析：

时间分析：{

枚举合法 k ，O()。

求合法 k 的数目：n 位不含有连续1的二进制数，设为 cnt(n)。

设 a[n] 表示 n 位不含有连续1且末位为1的二进制数数目，b[n] 表示 n 位不含有连续1且末位为0的二进制数数目。

则 cnt(n) = a[n] + b[n]。

其中 a[n] = b[n - 1]，b[n] = a[n - 1] + b[n - 1] = cnt(n - 1)。（前位为1则末位为0，前位为0则末尾任意）

则 cnt(n) = a[n] + b[n] = b[n - 1]+ a[n - 1] + b[n - 1] = cnt(n - 1) + b[n - 1] = cnt(n - 1) + cnt(n - 2)。

此乃斐波那契数列。考虑 cnt(1) = 2 = fib(3)，则 cnt(n) = fib(n + 2)。

fib(n)通项公式：

n趋于无穷大时，cnt(n) = $\frac{1}{\sqrt{5}}(\frac{1 + \sqrt{5}}{2}) ^{n + 2}$

共有m行，每行枚举两遍k，忽略常数项，O( $m(\frac{1 + \sqrt{5}}{2}) ^{n}$ )。

总时间复杂度 O( + $m(\frac{1 + \sqrt{5}}{2}) ^{n}$ )。

}

相邻两行递推

AcWing 327：

司令部的将军们打算在 N×M 的网格地图上部署他们的炮兵部队。

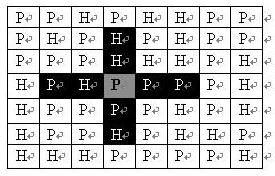
一个 N×M 的地图由 N 行 M 列组成，地图的每一格可能是山地（用 H 表示），也可能是平原（用 P 表示），如下图。

在每一格平原地形上最多可以布置一支炮兵部队（山地上不能够部署炮兵部队）；一支炮兵部队在地图上的攻击范围如图中黑色区域所示：

如果在地图中的灰色所标识的平原上部署一支炮兵部队，则图中的黑色的网格表示它能够攻击到的区域：沿横向左右各两格，沿纵向上下各两格。

图上其它白色网格均攻击不到。

从图上可见炮兵的攻击范围不受地形的影响。

现在，将军们规划如何部署炮兵部队，在防止误伤的前提下（保证任何两支炮兵部队之间不能互相攻击，即任何一支炮兵部队都不在其他支炮兵部队的攻击范围内），在整个地图区域内最多能够摆放多少我军的炮兵部队。

输入格式

第一行包含两个由空格分割开的正整数，分别表示 N 和 M；

接下来的 NN 行，每一行含有连续的 M 个字符(P 或者 H)，中间没有空格。按顺序表示地图中每一行的数据。

输出格式

仅一行，包含一个整数 K，表示最多能摆放的炮兵部队的数量。

数据范围

N≤100,M≤10

输入样例：
5 4
PHPP
PPHH
PPPP
PHPP
PHHP
输出样例：
6

这次变成了两行递推。

思路

只需要对上次的代码稍作修改。

dp[i & 1][k1][k2] 表示 [0, i] 行且第 i 行状态为 k1，第 i - 1 行状态为 k2 的最值。

三个约束：

k 要服从地图的约束，也就是第 i 行的合法 k 仅能是 g[i] 的子集。
k 内不含有相邻1或相间一个0，也就是行内需要合法。
第 i 行 k 也不能与 i - 1 行和 i - 2k 不含有相邻1，也就是两行间需要合法。

算法过程

行内合法的条件是： (k & (k >> 1) == 0 && (k & (k >> 2) == 0。

符合地图约束的k的条件：(k | g[i]) == g[i]。
行间合法的条件是：(k1 & k2) == 0 && (k1 & k3) == 0 && (k2 & k3) == 0 。

Code

#include <bits/stdc++.h>
using namespace std;
constexpr int N = 100, M = 10, MOD = 1e8;
int m, n, mx;
int g[N], dp[2][1 << M][1 << M], cnt[1 << M];
vector<int> st;
bool check(int k){return !(k & (k >> 1)) && !(k & (k >> 2));
}
bool check(int a, int b){return !(a & b);
}
int solve(){for (int k = 0; k <= mx; k++)if (check(k)) {st.push_back(k);cnt[k] = bitset<M>(k).count();}for (int k1 : st) if ((k1 | g[0])== g[0]) {dp[0][k1][0] = cnt[k1];for (int k2 : st) if ((k2 | g[1])== g[1] && check(k1, k2))dp[1][k2][k1] = cnt[k1] + cnt[k2];}for (int i = 2; i <= n + 1; i++)for (int k1 : st) if ((k1 | g[i]) == g[i])for (int k2 : st) if ((k2 | g[i - 1]) == g[i - 1] && check(k1, k2)) {dp[i & 1][k1][k2] = 0;for (int k3 : st) if ((k3 | g[i - 2]) == g[i - 2] && check(k1, k3) && check(k2, k3))dp[i & 1][k1][k2] = max(dp[i & 1][k1][k2], dp[(i - 1) & 1][k2][k3] + cnt[k1]);}return dp[(n + 1) & 1][0][0];
}
int main(){cin >> n >> m;  mx = (1 << m) - 1;for (int i = 0; i < n; i++)for (int j = 0; j < m; j++) {char x; cin >> x;g[i] |= ((x == 'P') << j);}cout << solve();return 0;
}

复杂度

时间复杂度: O( + $mT ^{n}$ )

空间复杂度: O( $2^{n}$ )

T：常数，1 < T < $\frac{1 + \sqrt{5}}{2}$

n：列数

m：行数

特殊优化：编译期计算

以第一题为例，我们知道 k 可以预处理得到，那能否更进步一些呢？

C++提供大量的静态计算支持，我们可以利用C++特性做一些工作。

我们直接在编译期计算 k 的合法状态，constexpr 函数会尝试进行编译期计算，我们传入编译期常量 N，就会在编译期直接生成出合法状态的数组。

虽然表面上我们是在编译期调用计算函数，但其实它已经算好了，已经储存在可执行程序中，这就省去了一个O()。

运行期由于每次数据范围不同，可以二分得到 k 的上界，然后正常计算即可。

constexpr int N = 13, MOD = 1e8;
int m, n, mx;
int g[N], dp[2][1 << N];
constexpr pair<array<int, 1 << N>, int> get_st(int MX){array<int, 1 << N> st{};int st_size = 0;for (int k = 0; k < MX; k++)if (!(k & (k >> 1)))st[st_size++] = k;return {st, st_size};
}
constexpr auto s = get_st(1 << N);
constexpr auto st = s.first;
constexpr auto st_size = s.second;
int solve(){int upper = upper_bound(st.begin(), st.begin() + st_size, mx) - st.begin();for (int k = 0; k < upper; k++)if ((st[k] | g[0]) == g[0])dp[0][st[k]] = 1;for (int i = 1; i <= m; i++)for (int k = 0; k < upper; k++) {dp[i & 1][st[k]] = 0;for (int pre_k = 0; pre_k < upper; pre_k++)if (!(st[k] & st[pre_k]) && (st[k] | g[i]) == g[i])dp[i & 1][st[k]] = (dp[i & 1][st[k]] + dp[(i - 1) & 1][st[pre_k]]) % MOD;}return dp[m & 1][0];
}