前言

你是不是对时间序列预测一脸懵？别担心！今天咱们来聊聊时间序列机器学习里超实用的一招——把时间序列变成特征，用过去的数据预测未来~ 本篇手把手教你用Python实现预测！

一、基本原理

1、啥是时间序列？

简单来说，时间序列预测就像是用过去的“故事”来猜测未来的“剧情”。想象一下，你每天记录自己的跑步速度，然后试图根据之前的速度来预测明天能跑多快。这就是时间序列预测的雏形。
比如每天的气温、股票价格、店铺销售额，这些按时间顺序排列的数据就是时间序列。

2、预测前的准备什么材料？

在正式预测之前，我们要把时间序列数据变一变，让它成为模型能“吃”的东西。这一步叫滞后嵌入（lag embedding）。打个比方，就像把一根长长的面条切成一小段一小段，方便我们一口一口地吃下去。
具体来说，就是从原始数据中创造出一些新的特征。比如，你现在的跑步速度可以和前几次的速度组合在一起，形成一个“特征套餐”。这个“套餐”里包含了过去的信息，能让模型更好地理解现在的状态和未来的趋势。

**核心思路：用过去的数值当特征，预测未来的值！**  
比如想预测明天的气温，咱们可以把昨天、前天、大前天的气温当作特征，这就是“滞后特征”（lag features）。

3、搭建你的预测工具（模型）

别被“模型”这个词吓到，它其实就是一种工具，帮你把那些“特征套餐”转化为预测结果。适合初学者的工具有很多，比如简单的线性回归模型。它就像一把尺子，帮你测量出未来的值大概在哪儿。
当然了，如果你想挑战一下，也可以试试更复杂的工具，比如决策树或者随机森林、线性回归、LSTM等。这些工具各有各的特点，你可以根据自己的数据和需求来选择(PS,写论文可以用到各种稀奇古怪的模型)。

二、建模模拟实战：用Python搭个简单模型

咱们先模拟一组时间序列数据，再一步步把它变成模型能用的特征——嵌入（Lag Embedding）

Step 1：先把需要的工具库准备好

import numpy as np  # 用于生成数据和数学计算
import pandas as pd  # 处理表格数据的核心库
from sklearn.linear_model import LinearRegression  # 导入线性回归模型
from sklearn.metrics import mean_squared_error  # 用于评估模型效果
import matplotlib.pyplot as plt  # 绘图工具
%matplotlib inline  # 让图表直接显示在代码下方（Jupyter notebook适用）
plt.style.use('seaborn-v0_8')  # 设置图表风格，更美观
# 设置中文字体支持
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用黑体显示中文
plt.rcParams['axes.unicode_minus'] = False  # 正常显示负号

💡 小提示： 如果是第一次用这些库，需要先在命令行输入 pip install numpy pandas scikit-learn matplotlib seaborn 安装哦~

Step 2：生成一组模拟的时间序列数据（带规律的）

np.random.seed(42)  # 固定随机种子，保证结果可复现
time = np.arange(1, 1001)  # 生成1到100的时间点（共100个数据点）# 生成带趋势、季节性和噪声的序列
# 0.5*time 是上升趋势，10*np.sin(time/10) 是周期性波动，后面是随机噪声
series = 0.5 * time + 10 * np.sin(time/10) + np.random.randn(1000) * 5# 把数据存到DataFrame里，方便后续处理
df = pd.DataFrame({'time': time, 'value': series})# 先看看数据长啥样（打印前5行）
print('数据前5行：')
print(df.head(5))

输出示例：

🧩 原理拆解：

• 趋势项（0.5*time）让数据整体随时间增长
• 季节项（sin函数）让数据有周期性波动（比如每周、每月的规律）
• 噪声项（randn）模拟真实数据中的随机波动

Step 3：写一个函数，专门用来创建滞后特征

def create_lag_features(df, target_col, lags):"""功能：给时间序列添加滞后特征列df: 输入的DataFrametarget_col: 目标列名（比如'value'）lags: 滞后阶数列表（比如[1,2,3]表示用前1、2、3天的值）"""lag_df = df.copy()  # 复制原始数据，避免修改原数据# 循环处理每个滞后阶数for lag in lags:# shift(lag)表示把数据向下移动lag行，相当于获取前lag个时间点的值# 比如lag=1时，第n行的lag_1是第n-1行的valuelag_df[f'lag_{lag}'] = lag_df[target_col].shift(lag)return lag_df# 调用函数，生成滞后特征（这里用滞后1、2、3步）
lags = [1, 2, 3]
df_lagged = create_lag_features(df, 'value', lags)# 看看添加滞后特征后的数据（前5行）
print('\n添加滞后特征后前5行：')
print(df_lagged.head(10))

输出示例：

⚠️ 注意点：

• 前3行（lag=1,2,3）因为没有足够的历史数据，所以lag列是NaN（需要后面删除）
• shift操作相当于“往前看”，比如lag=1就是用前一天的值作为今天的特征

Step 4：清洗数据 + 划分训练集和测试集（时间序列专属姿势！）

# 去掉所有包含NaN的行（前3行）
df_clean = df_lagged.dropna()
print(f'\n清洗后数据行数：{len(df_clean)}行（原100行，去掉3行NaN）')# 提取特征和目标值
X = df_clean[['lag_1', 'lag_2', 'lag_3']]  # 滞后特征作为输入
y = df_clean['value']  # 当天的值作为目标# 按时间顺序划分数据集（前80%训练，后20%测试）
train_size = int(0.8 * len(df_clean))
X_train, X_test = X[:train_size], X[train_size:]
y_train, y_test = y[:train_size], y[train_size:]print(f'\n训练集大小：{len(X_train)}行，测试集大小：{len(X_test)}行')

输出示例：

训练集大小：797行，测试集大小：200行

🚨 重要提醒：

• 时间序列绝对不能随机划分！必须按时间先后顺序，否则模型会“偷看到未来数据”
• 这里用80%作为训练集，是常见比例，也可以根据数据量调整（比如50%~90%）

Step 5：训练线性回归模型（最简单的机器学习模型）

# 创建线性回归模型对象
model = LinearRegression()# 用训练数据“教”模型（拟合参数）
model.fit(X_train, y_train)# 打印模型的系数（看看每个滞后特征的影响大小）
print('\n模型系数（权重）：')
for i, col in enumerate(X_train.columns):print(f'{col} 的权重：{model.coef_[i]:.4f}')
print(f'截距项：{model.intercept_:.4f}')

输出示例：

模型系数（权重）：
lag_1 的权重：0.3498
lag_2 的权重：0.3415
lag_3 的权重：0.3078
截距项：1.1149

📝 模型原理：
线性回归的公式是 y = w1*lag1 + w2*lag2 + w3*lag3 + b，其中：

• w1/w2/w3 是各个滞后特征的权重（上面的系数）
• b 是截距项（上面的intercept）
  模型训练的过程就是找到最合适的w和b，让预测值和真实值最接近

Step 6：用模型预测并评估效果（看看模型准不准）

# 用测试集数据预测
y_pred = model.predict(X_test)# 计算均方误差（MSE），值越小说明预测越准
mse = mean_squared_error(y_test, y_pred)
print(f'\n均方误差(MSE)：{mse:.2f}')# 把真实值和预测值放在一起对比
result_df = pd.DataFrame({'真实值': y_test.values,'预测值': y_pred
})
print('\n测试集前5个预测结果：')
print(result_df.head(5))

输出示例：

均方误差(MSE)：32.29测试集前5个预测结果：真实值         预测值
0  395.191982  391.701097
1  388.459700  392.632079
2  392.159406  392.085197
3  390.104435  392.613775
4  391.076101  391.086224

🔍 指标解释：

• 均方误差（MSE）是预测值与真实值差的平方的平均，反映整体误差大小
• 比如MSE=12.34，说明预测值和真实值的平均偏差大概是√12.34≈3.51（因为平方了，所以数值会比实际偏差大）

Step 7：可视化预测结果（用图表直观看看模型表现）

# 设置图片清晰度
plt.rcParams['figure.dpi'] = 300# 绘制真实值和预测值的对比图
plt.figure(figsize=(12, 6))
plt.plot(y_test.index, y_test, label='真实值', color='blue', linewidth=2)
plt.plot(y_test.index, y_pred, label='预测值', color='red', linestyle='--', linewidth=2)# 添加图表标题和标签
plt.title('时间序列预测结果对比', fontsize=15)
plt.xlabel('时间点', fontsize=12)
plt.ylabel('数值', fontsize=12)
plt.legend(fontsize=12)# 调整边框（去掉左右上三边边框，更简洁）
plt.gca().spines['left'].set_visible(False)
plt.gca().spines['right'].set_visible(False)
plt.gca().spines['top'].set_visible(False)# 添加网格线
plt.grid(axis='y', linestyle='--', alpha=0.7)plt.show()

图表效果：

🎨 图表解读：

• 蓝色实线是真实值的变化趋势
• 红色虚线是模型的预测值
• 两条线越接近，说明模型预测越准

Step 8：进阶操作：试试滑动窗口特征（让模型考虑近期趋势）

# 在原来的df_lagged里添加7天滑动平均特征
df_lagged['rolling_mean_7'] = df_lagged['value'].rolling(7).mean()# 再次清洗数据（前7行滑动平均有NaN）
df_clean_rolling = df_lagged.dropna()# 重新提取特征（加入滑动平均）
X_rolling = df_clean_rolling[['lag_1', 'lag_2', 'lag_3', 'rolling_mean_7']]
y_rolling = df_clean_rolling['value']# 划分训练测试集
train_size = int(0.8 * len(df_clean_rolling))
X_train_rolling, X_test_rolling = X_rolling[:train_size], X_rolling[train_size:]
y_train_rolling, y_test_rolling = y_rolling[:train_size], y_rolling[train_size:]# 训练新模型
model_rolling = LinearRegression()
model_rolling.fit(X_train_rolling, y_train_rolling)# 预测并计算MSE
y_pred_rolling = model_rolling.predict(X_test_rolling)
mse_rolling = mean_squared_error(y_test_rolling, y_pred_rolling)
print(f'\n加入滑动平均后的MSE：{mse_rolling:.2f}（原MSE：{mse:.2f}）')

可能的输出：
加入滑动平均后的MSE：23.09（原MSE：32.29）
📈 原理说明：
滑动平均能过滤短期噪声，突出近期趋势，比如：

• 当数据突然波动时，7天平均能让特征更稳定
• 适合处理有短期波动但长期趋势明显的数据

Tips小技巧

1. 滞后阶数怎么选？

   • 简单方法：先试小的阶数（比如1-5），看模型效果；
   • 专业点可以用“自相关函数（ACF）”看数据前后的相关性，选相关性高的滞后阶数。

2. 滑动窗口（Sliding Window）：
   如果想让模型考虑更近期的趋势，可以用滑动窗口取最近n个值的均值、最大值等作为特征，比如：

   df_lagged['rolling_mean_7'] = df_lagged['value'].rolling(7).mean()  # 7天滑动平均
   

3. 时间序列拆分注意事项：
   千万不能随机分训练测试集！必须按时间顺序，比如前80%训练，后20%测试，不然模型会“偷看”未来的数据，导致评估不准~

常见问题解决方案

1. 运行时报错“NameError: name ‘pd’ is not defined”？
   👉 检查是否忘记导入pandas（开头加 import pandas as pd）

2. 滞后特征全是NaN？
   👉 看看是否用了正确的shift参数，或者数据行数是否足够（比如lags=[1,2,3]至少需要4行数据）

3. 模型预测值全是同一个数？
   👉 可能是特征之间高度相关（多重共线性），可以减少滞后阶数，或者用随机森林模型

4. 想保存模型下次用？
   👉 可以用pickle库：import pickle; pickle.dump(model, open('time_series_model.pkl', 'wb'))

恭喜！你已经掌握了时间序列特征工程的核心技能

现在你可以用这套方法处理真实数据啦，记得多调整滞后阶数、试试不同模型（比如RandomForestRegressor），看看能不能让MSE更小！

三、常见问题避坑指南

• 数据平稳性问题： 如果时间序列有明显趋势（比如一直上涨），直接用滞后特征可能效果不好，需要先做差分（比如用今天的值减昨天的值）让数据平稳。
• 特征太多怎么办？ 滞后阶数太高会导致特征过多，可以用PCA降维，或者用随机森林等能自动筛选特征的模型。
• 真实场景怎么用？ 比如预测股票，可以结合成交量、大盘指数等其他特征一起喂给模型，效果更准~

四、总结：时间序列特征工程的核心逻辑

时间序列机器学习的关键就是把“时间规律”转化为模型能理解的特征，而滞后嵌入是最基础也最有效的方法之一。
记住：

1. 用过去n个时间点的值作为特征；
2. 按时间顺序划分训练测试集；
3. 根据数据特点调整滞后阶数和特征类型（滑动平均、差分等）。

请开启你的时间序列预测之旅吧。

所有代码：

# -*- coding: utf-8 -*-
"""
Created on Sat May 31 10:13:17 2025@author: 18268
"""import numpy as np
import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
import matplotlib.pyplot as plt
# 设置中文字体支持
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用黑体显示中文
plt.rcParams['axes.unicode_minus'] = False  # 正常显示负号# 1. 生成模拟时间序列（比如一个带有趋势和季节性的序列）
np.random.seed(42)
time = np.arange(1, 1001)
# 趋势 + 季节性 + 随机噪声
series = 0.5 * time + 10 * np.sin(time/10) + np.random.randn(1000) * 5
df = pd.DataFrame({'time': time, 'value': series})
print('数据前5行：')
print(df.head(5))
# 2. 构建滞后特征：这里我们用前3天的值作为特征
def create_lag_features(df, target_col, lags):lag_df = df.copy()# 对每个滞后阶数，创建新列for lag in lags:lag_df[f'lag_{lag}'] = lag_df[target_col].shift(lag)return lag_df# 生成滞后特征（滞后1、2、3步）
lags = [1, 2, 3]
df_lagged = create_lag_features(df, 'value', lags)
print(df_lagged.head(10))  # 看看数据长啥样# 3. 准备训练数据：注意时间序列不能随机划分，要按时间顺序！
# 去掉前3行（因为滞后特征前3行有NaN）
df_clean = df_lagged.dropna()
X = df_clean[['lag_1', 'lag_2', 'lag_3']]  # 特征
y = df_clean['value']  # 目标值# 划分训练集和测试集（比如前80%数据训练，后20%测试）
train_size = int(0.8 * len(df_clean))
X_train, X_test = X[:train_size], X[train_size:]
y_train, y_test = y[:train_size], y[train_size:]print(f'\n训练集大小：{len(X_train)}行，测试集大小：{len(X_test)}行')
# 4. 训练线性回归模型
model = LinearRegression()
model.fit(X_train, y_train)# 打印模型的系数（看看每个滞后特征的影响大小）
print('\n模型系数（权重）：')
for i, col in enumerate(X_train.columns):print(f'{col} 的权重：{model.coef_[i]:.4f}')
print(f'截距项：{model.intercept_:.4f}')
# 5. 预测并评估
y_pred = model.predict(X_test)
mse = mean_squared_error(y_test, y_pred)
print(f'均方误差(MSE): {mse:.2f}')# 把真实值和预测值放在一起对比
result_df = pd.DataFrame({'真实值': y_test.values,'预测值': y_pred
})
print('\n测试集前5个预测结果：')
print(result_df.head(5))# 6. 可视化预测结果（选做）plt.figure(figsize=(10, 6))
plt.plot(y_test.index, y_test, label='真实值')
plt.plot(y_test.index, y_pred, label='预测值', color='red', linestyle='--')
plt.legend()
plt.title('时间序列预测结果')
plt.show()# 在原来的df_lagged里添加7天滑动平均特征
df_lagged['rolling_mean_7'] = df_lagged['value'].rolling(7).mean()# 再次清洗数据（前7行滑动平均有NaN）
df_clean_rolling = df_lagged.dropna()# 重新提取特征（加入滑动平均）
X_rolling = df_clean_rolling[['lag_1', 'lag_2', 'lag_3', 'rolling_mean_7']]
y_rolling = df_clean_rolling['value']# 划分训练测试集
train_size = int(0.8 * len(df_clean_rolling))
X_train_rolling, X_test_rolling = X_rolling[:train_size], X_rolling[train_size:]
y_train_rolling, y_test_rolling = y_rolling[:train_size], y_rolling[train_size:]# 训练新模型
model_rolling = LinearRegression()
model_rolling.fit(X_train_rolling, y_train_rolling)# 预测并计算MSE
y_pred_rolling = model_rolling.predict(X_test_rolling)
mse_rolling = mean_squared_error(y_test_rolling, y_pred_rolling)
print(f'\n加入滑动平均后的MSE：{mse_rolling:.2f}（原MSE：{mse:.2f}）')

-----------------本篇完------------------

PS.扩展阅读

————————————————————————————————————————

对于python机器人编程感兴趣的小伙伴，可以进入如下链接阅读相关咨询

ps1.六自由度机器人相关文章资源

(1) 对六自由度机械臂的运动控制及python实现（附源码)

(2) N轴机械臂的MDH正向建模，及python算法

ps2.四轴机器相关文章资源

(1) 文章：python机器人编程——用python实现一个写字机器人

（2）python机器人实战——0到1创建一个自动是色块机器人项目-CSDN直播

(3)博文《我从0开始搭建了一个色块自动抓取机器人，并实现了大模型的接入和语音控制-(上基础篇)》的vrep基础环境
(3)博文《我从0开始搭建了一个色块自动抓取机器人，并实现了大模型的接入和语音控制-(上基础篇)》的vrep基础环境
(4)实现了语音输入+大模型指令解析+机器视觉+机械臂流程打通

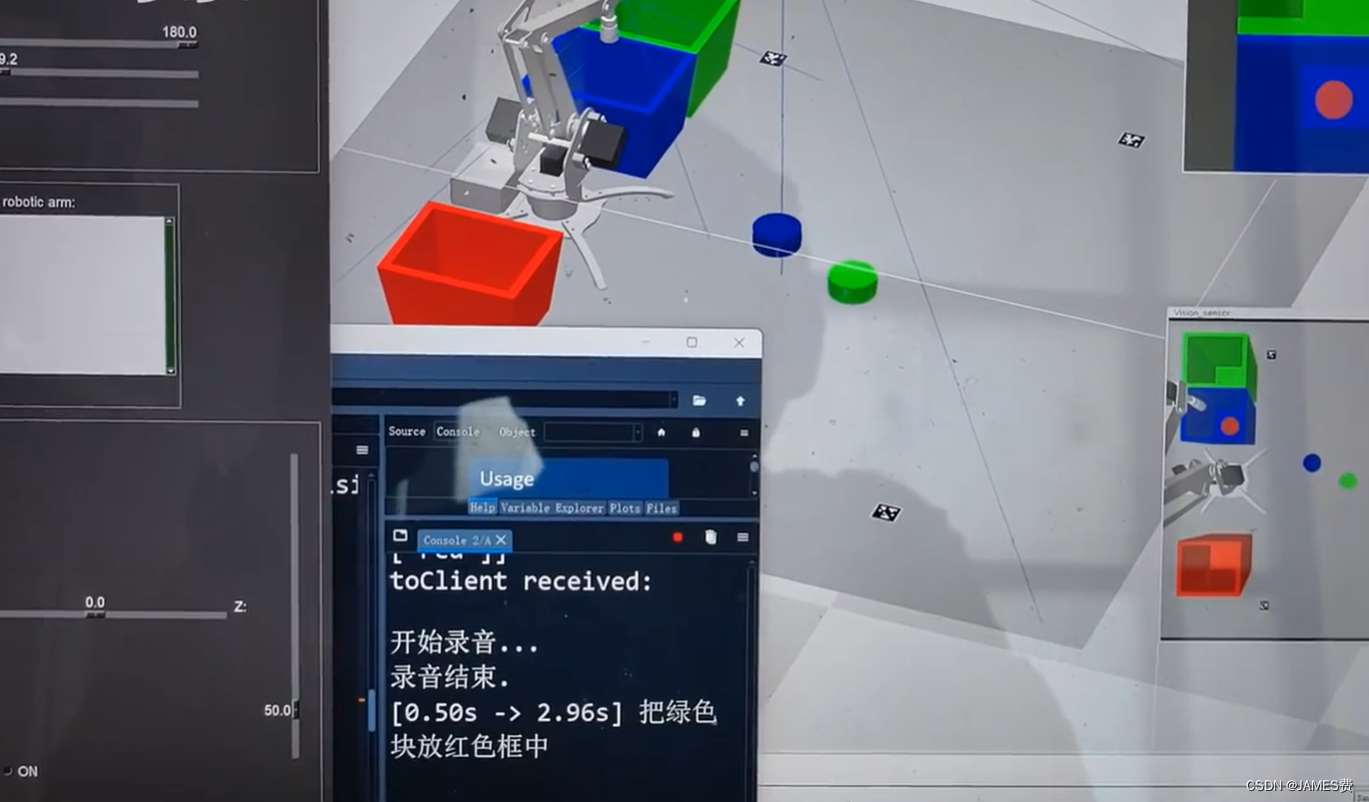
ps3.移动小车相关文章资源

（1）python做了一个极简的栅格地图行走机器人，到底能干啥？[第五弹]——解锁蒙特卡洛定位功能-CSDN博客
(2) 对应python资源：源码地址

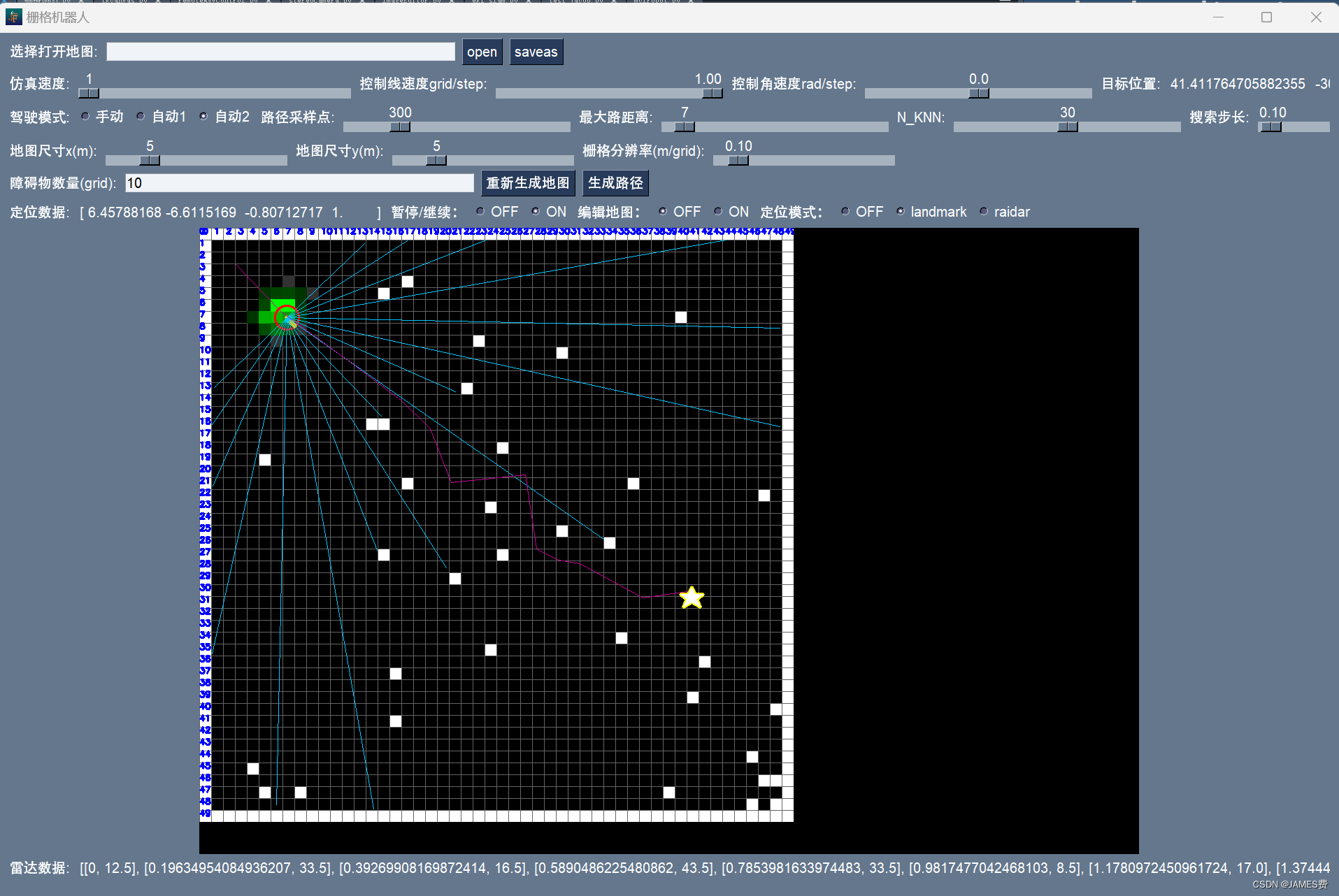
(3)python机器人编程——差速AGV机器、基于视觉和预测控制的循迹、自动行驶（上篇）_agv编程-CSDN博客
(4)python机器人编程——差速AGV机器、基于视觉和预测控制的循迹、自动行驶（下篇）_agv路线规划原则python-CSDN博客
对应python及仿真环境资源：源码链接

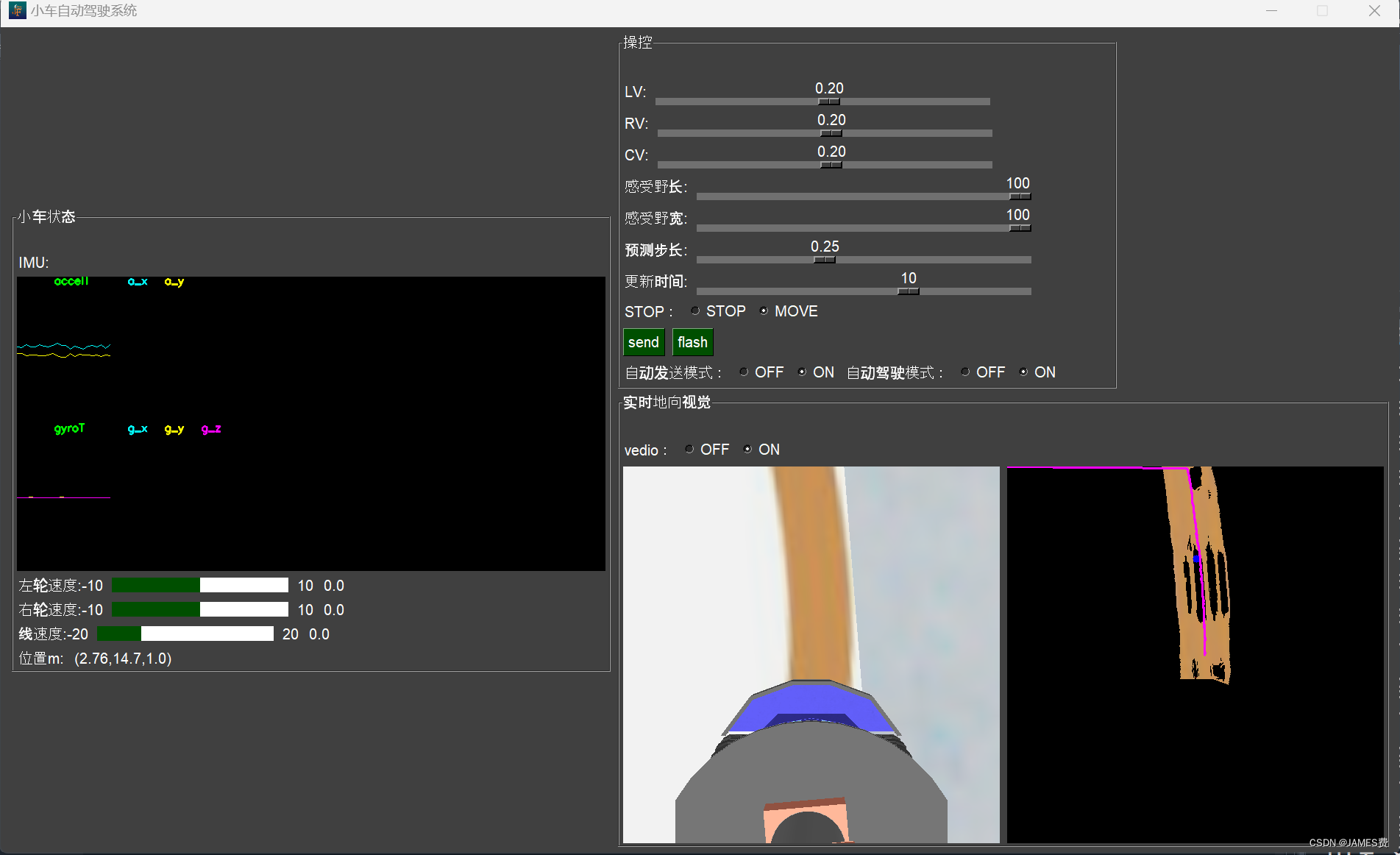
ps3.wifi小车控制相关文章资源

web端配套资源源代码已经上传(竖屏版)，下载地址
仿真配套资源已经上传：下载地址
web端配套资源源代码已经上传(横屏版)，下载地址