考察偏微分方程

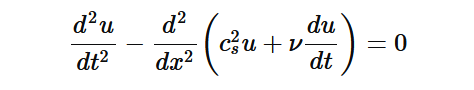
和初边值条件

这里主要示意一下，这个方程如何用Mathematica来求解以及在使用不同解法的时候，会遇到什么问题。

方法一：不额外附加边界条件

ClearAll[u, x, t, a, b, c, w, n];c = 1;
n = 1;
a = 1;
b = 1;
w = 1;pde = {D[u[t, x], t, t] - c*D[u[t, x], x, x] - n*D[v[t, x], t] == 0, v[t, x] == D[u[t, x], x, x]};
ics = {u[0, x] == 0, v[0, x] == 0, Derivative[1, 0][u][0, x] == 0};
bcs = {(D[u[t, x], x] /. x -> 0) == If[t <= 10^-6, 0, a*Sin[w*t] - b*Cos[w*t]], (D[u[t, x], x] /. x -> 1) == If[t <= 10^-6, 0, a*Sin[w*t] - b*Cos[w*t]]};{U, V} = NDSolveValue[{pde, ics, bcs}, {u, v}, {x, 0, 1}, {t, 0, 10}, Method -> {"IndexReduction" -> Automatic, "EquationSimplification" -> "Residual", "PDEDiscretization" -> {"MethodOfLines", "SpatialDiscretization" -> {"TensorProductGrid", "MinPoints" -> 141, "MaxPoints" -> 141, "DifferenceOrder" -> 2}}}]DensityPlot[U[t, x], {x, 0, 1}, {t, 0, 10}, ColorFunction -> "Rainbow",PlotLegends -> Automatic, FrameLabel -> Automatic]

这个时候，会遇到如下的问题提示。

但是依然能够绘制图形：

方法二：两次使用边界条件

ClearAll[u, x, t, a, b, c, w, n];c = 1;
n = 1;
a = 1;
b = 1;
w = 1;
f[t_] := If[t < 10^-6, 0, 1];
pde = {D[v[t, x], t] - c*D[u[t, x], x, x] - n*D[v[t, x], x, x] == 0, v[t, x] == D[u[t, x], t]};
ics = {u[0, x] == 0, v[0, x] == 0};
bcs = {(D[u[t, x], x] /. x -> 0) == (a*Sin[w*t] - b*Cos[w*t]) f[t], (D[u[t, x], x] /. x -> 1) == a*Sin[w*t] - b*Cos[w*t] f[t]};
bcs1 = {(D[v[t, x], x] /. x -> 0) == w (a*Cos[w*t] + b*Sin[w*t]) f[t], (D[v[t, x], x] /. x -> 1) == w (a*Cos[w*t] + b*Sin[w*t]) f[t]};{U, V} = NDSolveValue[{pde, ics, bcs, bcs1}, {u, v}, {x, 0, 1}, {t, 0, 10}, Method -> {"IndexReduction" -> Automatic, "EquationSimplification" -> "Residual", "PDEDiscretization" -> {"MethodOfLines", "SpatialDiscretization" -> {"TensorProductGrid", "MinPoints" -> 141, "MaxPoints" -> 141, "DifferenceOrder" -> 2}}}];{DensityPlot[U[t, x], {x, 0, 1}, {t, 0, 10}, ColorFunction -> "Rainbow", PlotLegends -> Automatic, FrameLabel -> Automatic, PlotLabel -> "u"], DensityPlot[V[t, x], {x, 0, 1}, {t, 0, 10}, ColorFunction -> "Rainbow", PlotLegends -> Automatic, FrameLabel -> Automatic, PlotLabel -> "v"]}

此时没有警告，并输出：