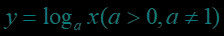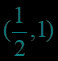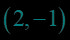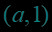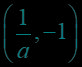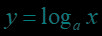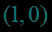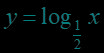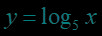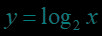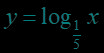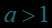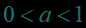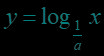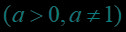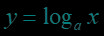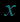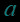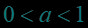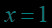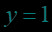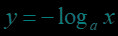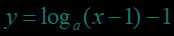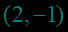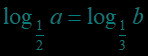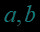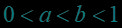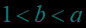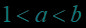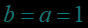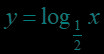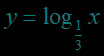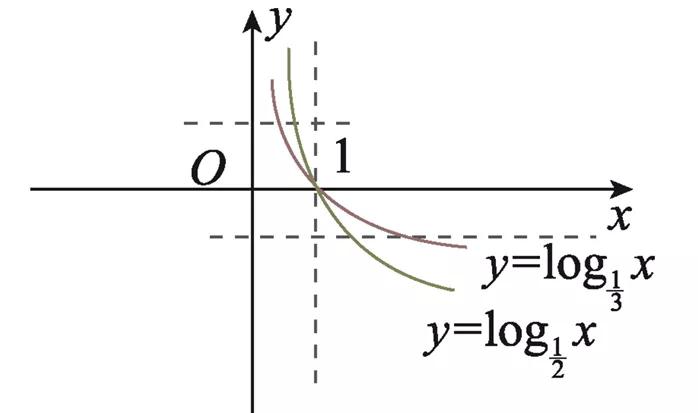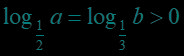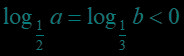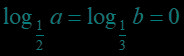人生就像弓箭,如果没有靶子,那么每天的拉弓练习就失去了意义。对数函数作为高考的重难点,同学们一定要熟练掌握呦!小本本记起来~~快和包学习APP打倒这个“大魔王”吧!
对数函数图象及其性质
01
对数函数的图象与性质
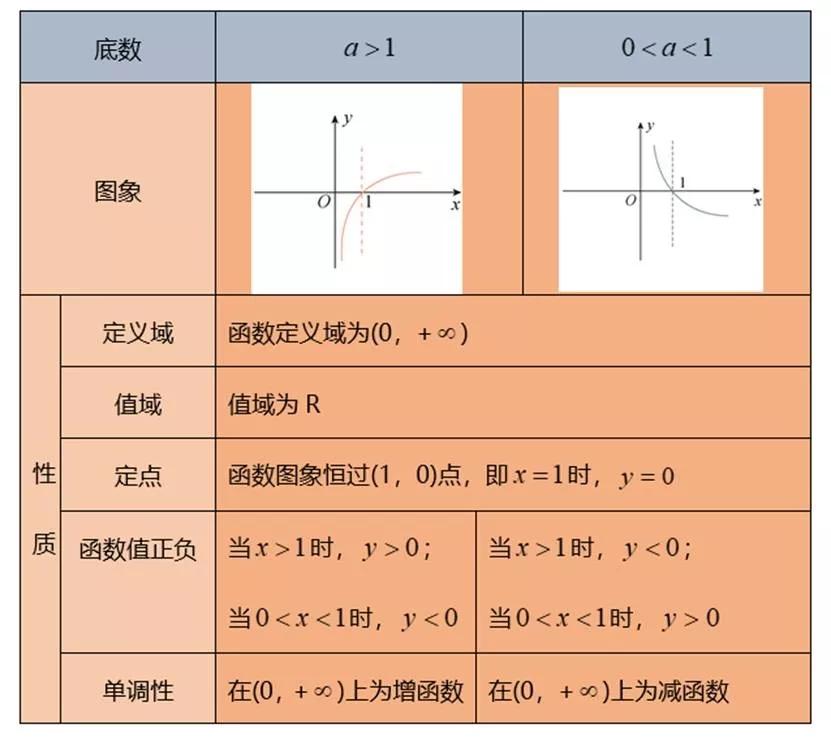
一般地,对数函数的图象和性质如下表:
02
对数函数图象的特征点
图象的特征点:,,,利用特征点可以快速作出对数函数的简图.如图象的特征点:,,.
03
底数对对数函数图象的影响
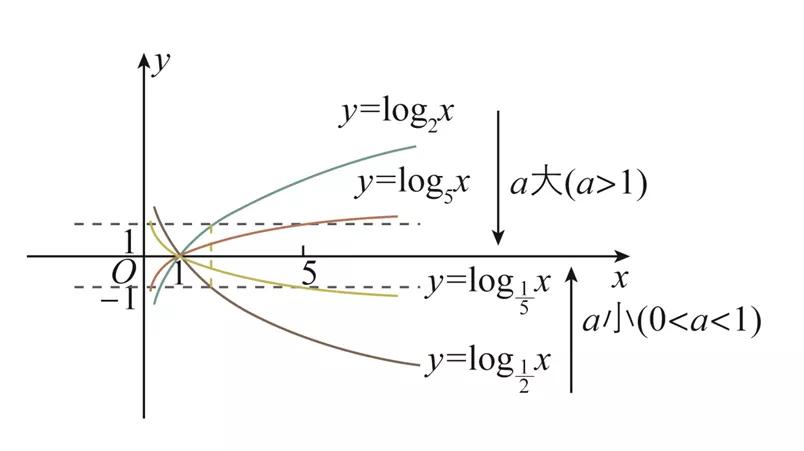
在同一直角坐标系中作出对数函数,,,的图象:
当时,动图展示如下:

当时,动图展示如下:
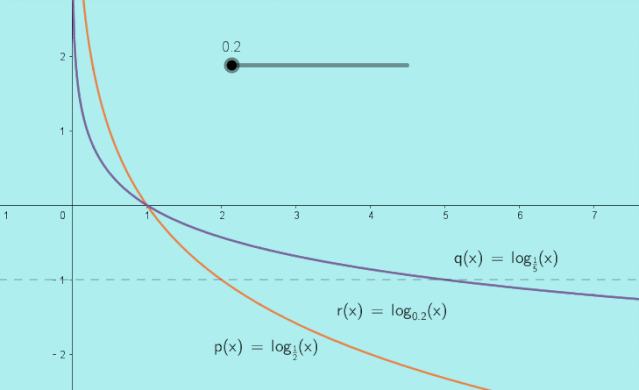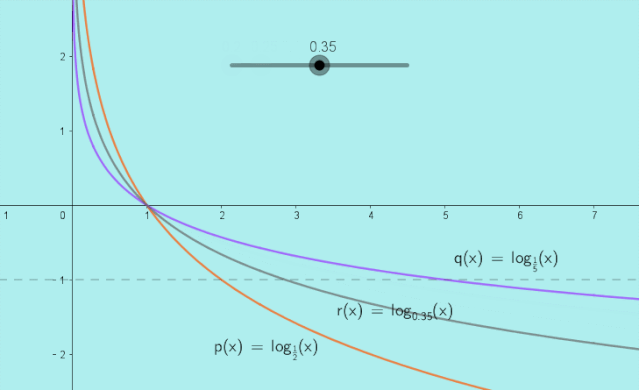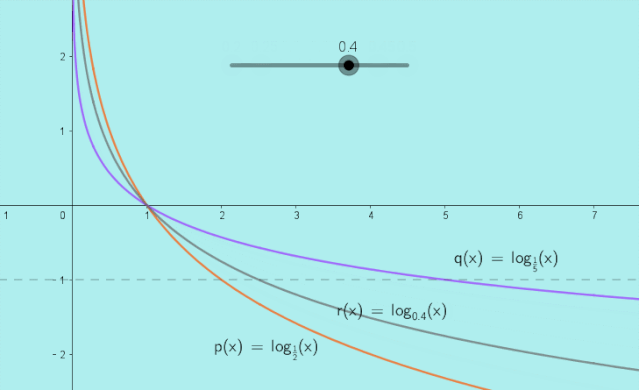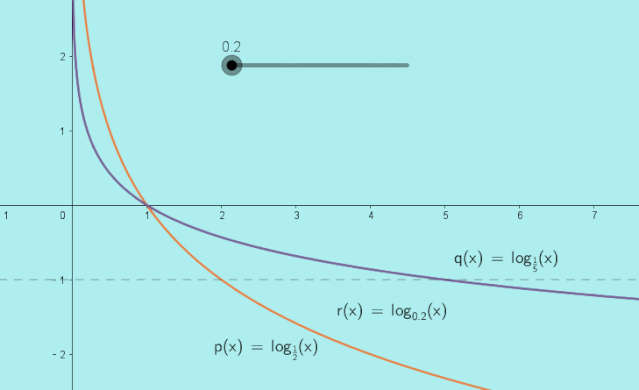
结论:
(1)函数与函数的图象关于轴对称.
(2)底数决定函数单调性:
,函数在(0,+)上为增函数,函数图象上升;
,函数在(0,+)上为减函数,函数图象下降.
(3)底数决定函数图象相对位置的高低:
①上下比较:在直线的右侧,时,越 大 ,图象越靠近轴;时,越小,图象越靠近轴.
②左右比较:比较图象与直线的交点,交点的横坐标越 大,对应的对数函数的底数越 大.
拓展:函数图象的对称性
(1)的图象可以看作将函数以代替,不变,因而两函数图象关于轴对称
(2)
(3)
【示范例题】
例题1.(填空题)函数
()的图象恒过点( ).
【答案】
【解析】当x=2时,恒有y=-1.
点拨
恒过定点问题:恒过定点的含义是函数值与无关,由=0知,令真数为1,可求解.
例题2.(填空题) 已知实数满足,则给出下面的五种关系,其中可能成立的序号为( ).
①;
②;
③;
④;
⑤
【答案】②④⑤
【解析】在同一坐标系中作函数与函数的图象如图,
若,则;
若,则;
若,则.
故②④⑤成立.
本文转载自包学习网站。
坚其志 苦其心 劳其力 事无大小,必有所成!
也许你感觉自己的努力总是徒劳无功 但包学习APP相信 你每天都离顶点更进一步
今天的你离顶点还遥遥无期 但你通过今天的努力
积蓄了明天勇攀高峰的力量