复数的指数形式:MATLAB演示
复数在工程和科学计算中无处不在,而指数形式(又称极坐标形式)是表示和处理复数的一种强大方式。本文将介绍复数的指数形式表示法,并展示如何使用MATLAB进行相关计算和可视化。
复数的基础回顾
复数通常表示为:
z = a + b i z = a + bi z=a+bi
其中:
- a a a 是实部
- b b b 是虚部
- i i i 是虚数单位,满足 i 2 = − 1 i^2 = -1 i2=−1
复数的指数形式
复数还可以表示为指数形式:
z = r e i θ = r ( cos θ + i sin θ ) z = re^{i\theta} = r(\cos\theta + i\sin\theta) z=reiθ=r(cosθ+isinθ)
其中:
- r = ∣ z ∣ = a 2 + b 2 r = |z| = \sqrt{a^2 + b^2} r=∣z∣=a2+b2 是模(绝对值)
- θ = atan2 ( b , a ) \theta = \text{atan2}(b, a) θ=atan2(b,a) 是幅角(相位角)
这个表示法基于欧拉公式:
e i θ = cos θ + i sin θ e^{i\theta} = \cos\theta + i\sin\theta eiθ=cosθ+isinθ
MATLAB中的复数表示
在MATLAB中,复数可以直接表示:
z = 3 + 4i; % 创建一个复数
或者使用复数函数:
z = complex(3, 4); % 等价于3 + 4i
转换为指数形式
我们可以计算模和幅角:
r = abs(z); % 计算模
theta = angle(z); % 计算幅角(弧度)
MATLAB中可以使用polarplot函数可视化:
polarplot([0 theta], [0 r], '-o');
title('复数在极坐标下的表示');
从指数形式恢复直角坐标形式
a = r cos θ a = r \cos\theta a=rcosθ
b = r sin θ b = r \sin\theta b=rsinθ
z = a + b i z = a + bi z=a+bi
MATLAB实现:
a = r * cos(theta); % 实部
b = r * sin(theta); % 虚部
z_recovered = a + b*1i;
MATLAB演示示例
figure;
subplot(1,2,1);
hold on
quiver(0, 0, real(z), imag(z), 0, ...'b-.', 'LineWidth', 2,'MaxHeadSize',0.4); % 绘制 z1 的向量
plot(real(z), imag(z), 'ro', 'MarkerSize', 10, 'MarkerFaceColor', 'r');
xlim([0 2]); ylim([0 2]);
grid on;
xlabel('实部'); ylabel('虚部');
title('直角坐标表示');
hold offsubplot(1,2,2);
polarplot([0 theta], [0 r], '-o');
title('极坐标表示');% 验证欧拉公式
fprintf('直角坐标形式: %.4f + %.4fi\n', real(z), imag(z));
fprintf('指数形式恢复: %.4f + %.4fi\n', r*cos(theta), r*sin(theta));
运行结果:
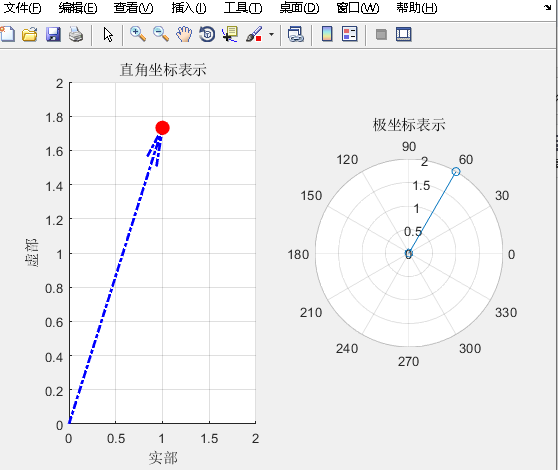
复数运算的指数形式优势
- 乘法:
z 1 ⋅ z 2 = r 1 r 2 e i ( θ 1 + θ 2 ) z_1 \cdot z_2 = r_1r_2 e^{i(\theta_1+\theta_2)} z1⋅z2=r1r2ei(θ1+θ2)
z1 = 2*exp(1i*pi/4);
z2 = 3*exp(1i*pi/6);
z_product = z1 * z2; % 6*exp(1i*(pi/4+pi/6))
- 除法:
z 1 z 2 = r 1 r 2 e i ( θ 1 − θ 2 ) \frac{z_1}{z_2} = \frac{r_1}{r_2} e^{i(\theta_1-\theta_2)} z2z1=r2r1ei(θ1−θ2)
z_quotient = z1 / z2; % (2/3)*exp(1i*(pi/4-pi/6))
- 幂运算:
z n = r n e i n θ z^n = r^n e^{i n\theta} zn=rneinθ
n = 3;
z_power = z1^n; % 2^n * exp(1i*n*pi/4)
应用实例:旋转操作
复数乘法可以表示旋转:
z rotated = z ⋅ e i α z_{\text{rotated}} = z \cdot e^{i\alpha} zrotated=z⋅eiα
% 原始复数
z = 2 + 1i;% 逆时针旋转45度(π/4弧度)
rotation = exp(1i*pi/4);
z_rotated = z * rotation;% 可视化
figure;
compass(real(z), imag(z), 'r'); hold on;
compass(real(z_rotated), imag(z_rotated), 'b');
legend('原始复数', '旋转后复数');
title('复数旋转演示');
运行结果:
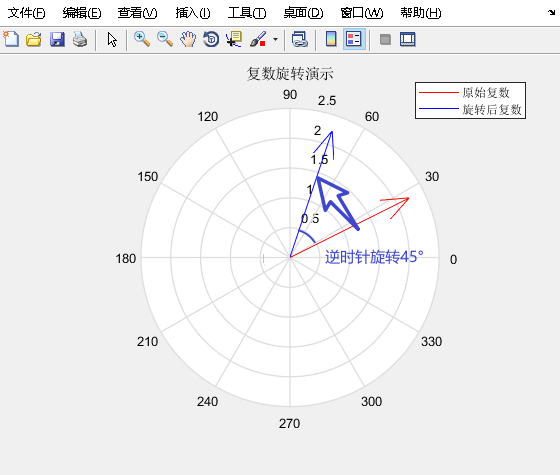
结语
复数的指数形式 z = r e i θ z = re^{i\theta} z=reiθ 不仅提供了复数的一种简洁表示,还大大简化了许多运算。通过MATLAB的可视化和计算功能,我们可以更直观地理解复数运算的几何意义。