中心对称与中心对称图形
中心对称的定义:
把一个图形绕着某一点旋转180°,如果它能与另一个图形重合,就说这两个图形关于这个点对称.
中心对称的性质:
(1)关于中心对称的两个图形是全等形
(2)关于中心对称的两个图形,对称点连线都经过对称中心且被对称中心平分
已知四边形ABCD和点O(下图),画四边形A’B’C’D’,使它与已知四边形关于点O对称.
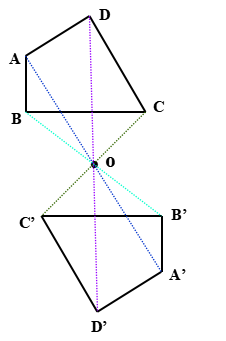
画法:
1. 连结AO并延长到A’,使OA’=OA,得到点A的对称点A’.
2. 同样画B、C、D的对称点
B’、C’、D’.
3. 顺次连结A’、B’、C’、D’各点.
四边形A’B’C’D’就是所求的四边形.
3.中心对称的判定:
如果两个图形对应点连线 都经过某一点,并且被在个点平分那么这两个图形关于这一点对称。
4.中心对称图形的定义
把一个图形绕着某一点旋转180°,如果旋转后的图形能够和原来的图形相互重合,那么这个图形叫中心对称图形。
5.中心对称与中心对称图形的联系和区别
区别:
中心对称指两个全等图形的相互位置关系
中心对称图形指一个图形本身成中心对称
联系:
如果将中心对称图形的两个图形看成一个整体,则它们是中心对称图形
如果将中心对称图形,把对称的部分看成两个图形,则它们是关于中心对称。
6.中心对称图形与轴对称图形的不同之处为:

1判断下列各图形是否是中心对称图形?为什么?
⑴平行四边形
⑵等边三角形
⑶线段
解:
⑴∵平行四边形的对角线互相平分
∴相对的两个顶点都关于对角线交点对称
∴平行四边形是中心对称图形
⑵∵等边三角形设有对称中心
∴等边三角形不是中心对称图形
⑶∵线段的中心是对称中心
∴线段是中心对称图形